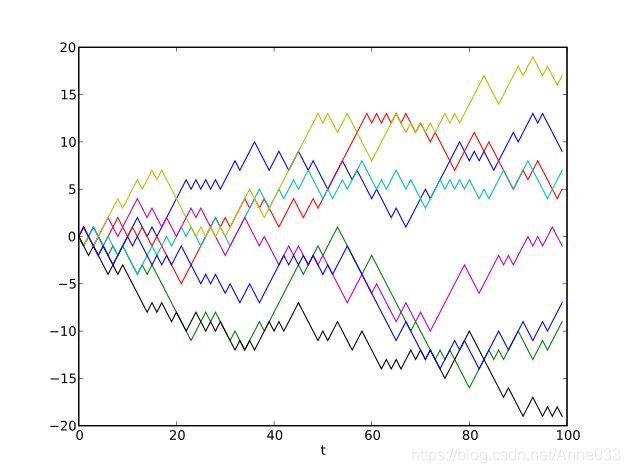
随机游走（英语：Random Walk，缩写为 RW），是一种数学统计模型，它是一连串的轨迹所组成，其中每一次都是随机的。[1][2]它能用来表示不规则的变动形式，如同一个人酒后乱步，所形成的随机过程记录。1905年，由卡尔·皮尔逊首次提出。[3]

随机游走可以在各种空间上进行：通常研究的包括图，整数或实数线，向量空间，曲面，高维的黎曼流形，以及群，有限生成群或李群。在最简单的情况中，时间是离散的，随机游走的路径为一个由自然数索引的随机变量序列(Xt) = (X1, X2, …)。但是，也可以定义在随机时间采取步骤的随机游走，在这种情况下，必须定义X
t的所有时间t ∈ [0,+∞)。

通常，我们可以假设随机游走是以马尔可夫链或马可夫过程的形式出现，但是比较复杂的随机游走则不一定以这种形式出现。在某些限制条件下，会出现一些比较特殊的模式，如扩散作用的模型布朗运动，醉汉走路（drunkard’s walk）或莱维飞行。

随机游走在各个领域有许多应用，例如在工程学和许多科学领域，包括生态学，心理学，计算机科学，物理，化学，生物学以及经济学。在数学中，我们可以用个体为本模型的随机游走来估算π的值。它可以用来模拟分子在液体或气体中传播时的路径，觅食动物的搜索路径，波动的股票价格和赌徒的财务状况。在这些领域中，随机游走可以用来解释许多观察到的现象，因此它是记录随机活动的基本统计模型。[1]

https://zh.wikipedia.org/wiki/%E9%9A%A8%E6%A9%9F%E6%BC%AB%E6%AD%A5