时间序列及其预测是日常工作中建模，分析，预测的重要组成部分。

本文我们将从0开始介绍时间序列的含义，模型及其分析及其常用的预测模型。

交流

本文来自技术群小伙伴分享的，技术交流欢迎入群

目前开通了技术交流群，群友已超过3000人，添加时最好的备注方式为：来源+兴趣方向，方便找到更快获取资料、入群

方式①、添加微信号：dkl88191，备注：来自CSDN+加群
方式②、微信搜索公众号：Python学习与数据挖掘，后台回复：加群

时间序列定义

时间序列是按照一定的时间间隔排列的一组数据，其时间间隔可以是任意的时间单位，如小时、日、周月等。比如，每天某产品的用户数量，每个月的销售额，这些数据形成了以一定时间间隔的数据。

通过对这些时间序列的分析，从中发现和揭示现象发展变化的规律，并将这些知识和信息用于预测。比如销售量是上升还是下降，销售量是否与季节有关，是否可以通过现有的数据预测未来一年的销售额是多少等。

对于时间序列的预测，由于很难确定它与其他变量之间的关系，这时我们就不能用回归去预测，而应使用时间序列方法进行预测。

采用时间序列分析进行预测时需要一系列的模型，这种模型称为时间序列模型。

时间序列预测模型与方法

注：本部分只关注相关模型与分析的方法，模型的选择，调参与优化会放在后续文章中详细讲解

原始数据

本文所使用原始数据与代码，可以在公众号：Smilecoc的杂货铺 中回复“时间序列”获取。可直接扫描文末二维码关注！

朴素法

朴素法就是预测值等于实际观察到的最后一个值。它假设数据是平稳且没有趋势性与季节性的。通俗来说就是以后的预测值都等于最后的值。

这种方法很明显适用情况极少，所以我们重点通过这个方法来熟悉一下数据可视化与模型的评价及其相关代码。

#朴素法
dd = np.asarray(train['Count'])#训练组数据
y_hat = test.copy()#测试组数据
y_hat['naive'] = dd[len(dd) - 1]#预测组数据#数据可视化
plt.figure(figsize=(12, 8))
plt.plot(train.index, train['Count'], label='Train')
plt.plot(test.index, test['Count'], label='Test')
plt.plot(y_hat.index, y_hat['naive'], label='Naive Forecast')
plt.legend(loc='best')
plt.title("Naive Forecast")
plt.show()

得到结果：

我们通过计算均方根误差，检查模型在测试数据集上的准确率。
其中均方根误差（RMSE）是各数据偏离真实值的距离平方和的平均数的开方

#计算均方根误差RMSE
from sklearn.metrics import mean_squared_error
from math import sqrt# mean_squared_error求均方误差
rmse = sqrt(mean_squared_error(test['Count'], y_hat['naive']))
print(rmse)

得到均方根误差为1053

简单平均法

简单平均法就是预测的值为之前过去所有值的平均.当然这不会很准确，但这种预测方法在某些情况下效果是最好的。

#简单平均法
y_hat_avg = test.copy()
y_hat_avg['avg_forecast'] = train['Count'].mean()

其后续可视化与模型效果评估方法与上述一致，这里不再赘述，需要详细代码可以查看相关源码。得到RMSE值为2637

移动平均法

我们经常会遇到这种数据集，比如价格或销售额某段时间大幅上升或下降。如果我们这时用之前的简单平均法，就得使用所有先前数据的平均值，但在这里使用之前的所有数据是说不通的，因为用开始阶段的价格值会大幅影响接下来日期的预测值。因此，我们只取最近几个时期的价格平均值。很明显这里的逻辑是只有最近的值最要紧。这种用某些窗口期计算平均值的预测方法就叫移动平均法。

#移动平均法
y_hat_avg = test.copy()
#利用时间窗函数rolling求平均值u
y_hat_avg['moving_avg_forecast'] = train['Count'].rolling(60).mean().iloc[-1]

其后续可视化与模型效果评估方法与上述一致，这里不再赘述，需要详细代码可以查看相关源码。得到RMSE值为1121

指数平滑法

在做时序预测时，一个显然的思路是：认为离着预测点越近的点，作用越大。比如我这个月体重100斤，去年某个月120斤，显然对于预测下个月体重而言，这个月的数据影响力更大些。假设随着时间变化权重以指数方式下降——最近为0.8，然后0.8**2，0.8**3…，最终年代久远的数据权重将接近于0。将权重按照指数级进行衰减，这就是指数平滑法的基本思想。

指数平滑法有几种不同形式：一次指数平滑法针对没有趋势和季节性的序列，二次指数平滑法针对有趋势但没有季节性的序列，三次指数平滑法针对有趋势也有季节性的序列。“

所有的指数平滑法都要更新上一时间步长的计算结果，并使用当前时间步长的数据中包含的新信息。它们通过”混合“新信息和旧信息来实现，而相关的新旧信息的权重由一个可调整的参数来控制。

一次指数平滑

一次指数平滑法的递推关系如下：

可以看出，在指数平滑法中，所有先前的观测值都对当前的平滑值产生了影响，但它们所起的作用随着参数 α \alpha α 的幂的增大而逐渐减小。那些相对较早的观测值所起的作用相对较小。同时，称α为记忆衰减因子可能更合适——因为α的值越大，模型对历史数据“遗忘”的就越快。从某种程度来说，指数平滑法就像是拥有无限记忆（平滑窗口足够大）且权值呈指数级递减的移动平均法。一次指数平滑所得的计算结果可以在数据集及范围之外进行扩展，因此也就可以用来进行预测。预测方式为：

我们可以通过statsmodels中的时间序列模型进行指数平滑建模。官方文档地址为：
https://www.statsmodels.org/stable/generated/statsmodels.tsa.holtwinters.SimpleExpSmoothing.html
具体代码如下：

#一次指数平滑
from statsmodels.tsa.api import SimpleExpSmoothingy_hat_avg = test.copy()
fit = SimpleExpSmoothing(np.asarray(train['Count'])).fit(smoothing_level=0.6, optimized=False)
y_hat_avg['SES'] = fit.forecast(len(test))

之后同样进行数据可视化并查看模型效果

plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SES'], label='SES')
plt.legend(loc='best')
plt.show()

可视化结果为：

RMSE结果为1040

二次指数平滑

在介绍二次指数平滑前介绍一下趋势的概念。

之后使用二次指数平滑进行预测：

from statsmodels.tsa.api import Holty_hat_avg = test.copy()fit = Holt(np.asarray(train['Count'])).fit(smoothing_level=0.3, smoothing_slope=0.1)
y_hat_avg['Holt_linear'] = fit.forecast(len(test))

结果如图：

得到对应的RMSE为1033

三次指数平滑

在应用这种算法前，我们先介绍一个新术语。假如有家酒店坐落在半山腰上，夏季的时候生意很好，顾客很多，但每年其余时间顾客很少。因此，每年夏季的收入会远高于其它季节，而且每年都是这样，那么这种重复现象叫做“季节性”（Seasonality）。如果数据集在一定时间段内的固定区间内呈现相似的模式，那么该数据集就具有季节性。

二次指数平滑考虑了序列的基数和趋势，三次就是在此基础上增加了一个季节分量。类似于趋势分量，对季节分量也要做指数平滑。比如预测下一个季节第3个点的季节分量时，需要指数平滑地考虑当前季节第3个点的季节分量、上个季节第3个点的季节分量…等等。详细的有下述公式(累加法)：

在使用二次平滑模型与三次平滑模型前，我们可以使用sm.tsa.seasonal_decompose分解时间序列，可以得到以下分解图形——从上到下依次是原始数据、趋势数据、周期性数据、随机变量（残差值）

根据分析图形和数据可以确定对应的季节参数

具体代码为：

#三次指数平滑
from statsmodels.tsa.api import ExponentialSmoothingy_hat_avg = test.copy()
fit1 = ExponentialSmoothing(np.asarray(train['Count']), seasonal_periods=7, trend='add', seasonal='add', ).fit()
y_hat_avg['Holt_Winter'] = fit1.forecast(len(test))

得到的RMSE为575。我们可以看到趋势和季节性的预测准确度都很高。你可以试着调整参数来优化这个模型。

AR模型

MA模型

ARMA模型

ARMA(Auto Regressive and Moving Average Model)自回归移动平均模型是与自回归和移动平均模型两部分组成。所以可以表示为ARMA(p, q)。p是自回归阶数，q是移动平均阶数。

从式子中就可以看出，自回归模型结合了两个模型的特点，其中，AR可以解决当前数据与后期数据之间的关系，MA则可以解决随机变动也就是噪声的问题。

ARIMA模型

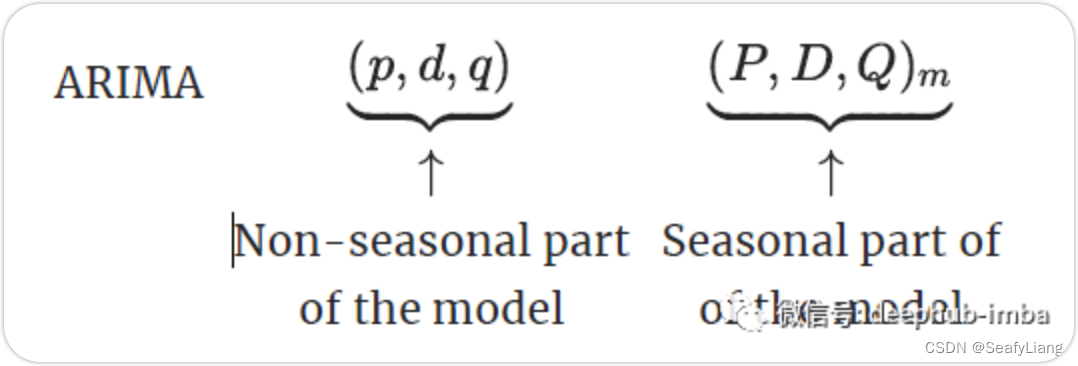
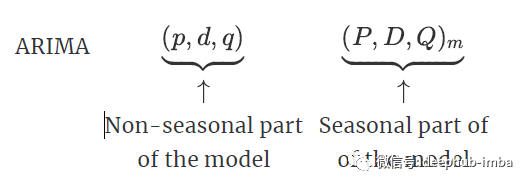
ARIMA(Auto Regressive Integrate Moving Average Model)差分自回归移动平均模型是在ARMA模型的基础上进行改造的，ARMA模型是针对t期值进行建模的，而ARIMA是针对t期与t-d期之间差值进行建模，我们把这种不同期之间做差称为差分，这里的d是几就是几阶差分。ARIMA模型也是基于平稳的时间序列的或者差分化后是稳定的，另外前面的几种模型都可以看作ARIMA的某种特殊形式。表示为ARIMA(p, d, q)。p为自回归阶数，q为移动平均阶数，d为时间成为平稳时所做的差分次数，也就是Integrate单词的在这里的意思。

具体步骤如下：

使用ARIMA进行预测代码如下：

from statsmodels.tsa.arima_model import ARIMAts_ARIMA= train['Count'].astype(float)
fit1 = ARIMA(ts_ARIMA, order=(7, 1, 4)).fit()
y_hat_ARIMA = fit1.predict(start="2013-11-1", end="2013-12-31", dynamic=True)

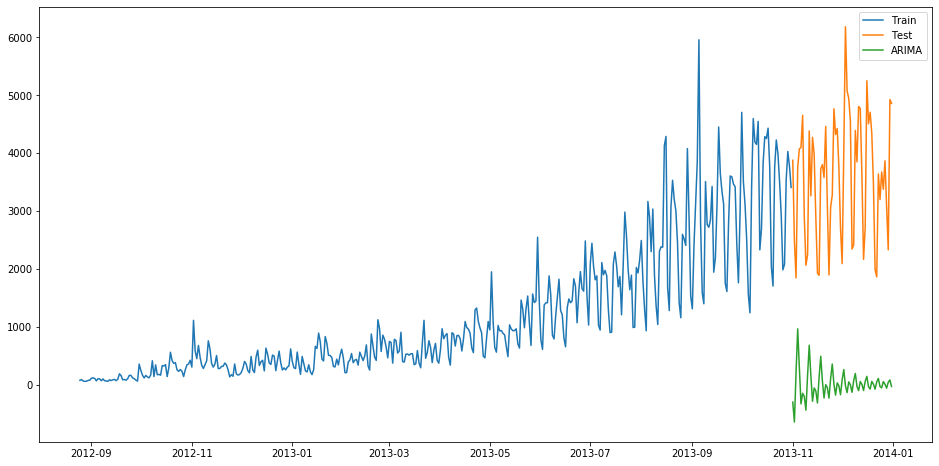
并画出预测值与实际值图形：

plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_ARIMA, label='ARIMA')
plt.legend(loc='best')
plt.show()

并计算RMSE:

from sklearn.metrics import mean_squared_error
from math import sqrtrmse = sqrt(mean_squared_error(test['Count'],y_hat_ARIMA.to_frame()))
print(rmse)

得到对应的RMSE为3723

SARIMA模型

SARIMA季节性自回归移动平均模型模型在ARIMA模型的基础上添加了季节性的影响，结构参数有七个：SARIMA(p,d,q)(P,D,Q,s)
其中p,d,q分别为之前ARIMA模型中我们所说的p:趋势的自回归阶数。d:趋势差分阶数。q:趋势的移动平均阶数。
P:季节性自回归阶数。
D:季节性差分阶数。
Q:季节性移动平均阶数。
s:单个季节性周期的时间步长数。

import statsmodels.api as sm
y_hat_avg = test.copy()
fit1 = sm.tsa.statespace.SARIMAX(train.Count, order=(2, 1, 4), seasonal_order=(0, 1, 1, 7)).fit()
y_hat_avg['SARIMA'] = fit1.predict(start="2013-11-1", end="2013-12-31", dynamic=True)

得到实际值与预测值如下：

plt.figure(figsize=(16, 8))
plt.plot(train['Count'], label='Train')
plt.plot(test['Count'], label='Test')
plt.plot(y_hat_avg['SARIMA'], label='SARIMA')
plt.legend(loc='best')
plt.show()

并计算RMSE：

from sklearn.metrics import mean_squared_error
from math import sqrt
rmse = sqrt(mean_squared_error(test['Count'], y_hat_avg['SARIMA']))
print(rmse)

结果为933

其他时间序列预测的模型还有SARIMAX模型（在ARIMA模型上加了季节性的因素），Prophet模型，ARCH模型，LSTM神经网络模型等。限于篇幅，感兴趣的同学可以自行查看相关模型资料

在后续的文章中我们将讲解如何确定数据的平稳性与数据预处理，为后续时间序列的建模做准备