import pandas as pd#取数
#df=pd.read_csv('jetrail.csv')
#print(df.head())
'''ID          Datetime  Count
0   0  25-08-2012 00:00      8
1   1  25-08-2012 01:00      2
2   2  25-08-2012 02:00      6
3   3  25-08-2012 03:00      2
4   4  25-08-2012 04:00      2
'''
#print(df.shape) #(18288, 3)
#2012-2014年数据，将小时统计转换成以天为单位的聚合数据集
#前 14 个月（ 2012 年 8 月- 2013 年 10 月）用作训练数据，后两个月（2013 年 11 月 – 2013 年 12 月）用作测试数据。

数据准备

#1、数据准备
df=pd.read_csv('jetrail.csv',nrows=11856)
train=df[:10392]
test=df[10392:]df['Timestamp']=pd.to_datetime(df.Datetime,format='%d-%m-%Y %H:%M')# 4位年用Y，2位年用y
df.index=df.Timestamp   #将日期设为索引
df=df.resample('D').mean()
#重新采样，是对原样本重新处理的一个方法，是一个对常规时间序列数据重新采样和频率转换的便捷的方法。
#降采样：高频数据到低频数据      升采样：低频数据到高频数据
train['Timestamp']=pd.to_datetime(train.Datetime,format='%d-%m-%Y %H:%M')# 4位年用Y，2位年用y
train.index=train.Timestamp   #将日期设为索引
train=train.resample('D').mean()test['Timestamp']=pd.to_datetime(test.Datetime,format='%d-%m-%Y %H:%M')# 4位年用Y，2位年用y
test.index=test.Timestamp   #将日期设为索引
test=test.resample('D').mean()#将整个数据集、训练集、测试集都进行按天的频度重新采样

数据可视化

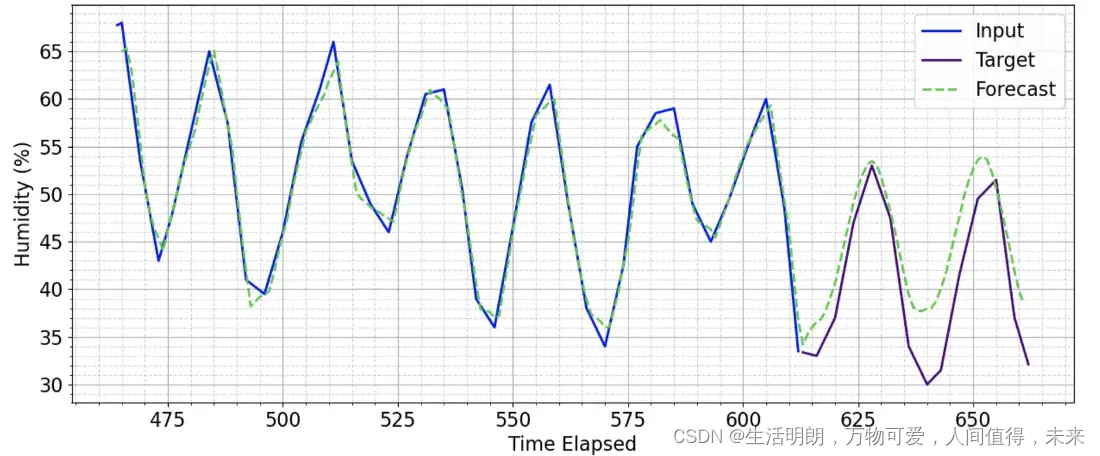
#2、数据可视化
import matplotlib.pyplot as plt
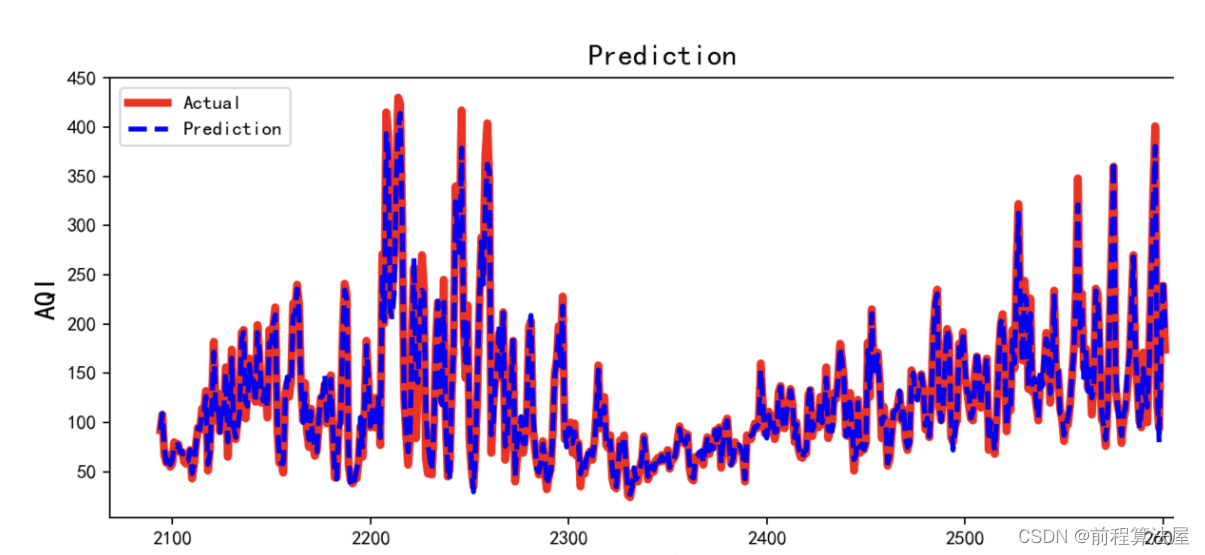
train.Count.plot(figsize=(16,10),title='Daily Ridership',fontsize=14)
test.Count.plot(figsize=(16,10),title='Daily Ridership',fontsize=14)
plt.show()

方法一、朴素法

'''
1、朴素法：最适合稳定性很高的数据集。如果数据集在一段时间内都很稳定，我们想预测第二天的价格，可以取前面一天的价格，预测第二天的值。
这种假设第一个预测点和上一个观察点相等的预测方法就叫朴素法。即 yt+1^=yt
'''
count_col=train.Count
y_hat=test.copy()
y_hat['naive']=count_col[-1]
train.Count.plot(figsize=(16,10),title='Daily Ridership',fontsize=14)
test.Count.plot(figsize=(16,10),title='Daily Ridership',fontsize=14)
y_hat.naive.plot(figsize=(16,10),title='Daily Ridership',fontsize=14)
plt.legend(loc='best')
plt.title('naive forecast')
plt.show()#用均方根误差算准确率
from sklearn.metrics import mean_squared_error
from math import sqrtrms1=sqrt(mean_squared_error(test.Count,y_hat.naive))
print("朴素法",rms1)

方法二、简单平均法

'''
2、简单平均法：物品价格会随机上涨和下跌，平均价格会保持一致。我们经常会遇到一些数据集，
虽然在一定时期内出现小幅变动，但每个时间段的平均值确实保持不变。
将预期值等同于之前所有观测点的平均值的预测方法就叫简单平均法。
'''
y_hat_avg=test.copy()
y_hat_avg["avg_forecast"]= train.Count.mean()
train.Count.plot(figsize=(16,10),title='average forecast',fontsize=14)
test.Count.plot(figsize=(16,10),title='average forecast',fontsize=14)
y_hat_avg.avg_forecast.plot(figsize=(16,10),title='average forecast',fontsize=14)
plt.legend(loc='best')
plt.show()
rms2=sqrt(mean_squared_error(test.Count,y_hat_avg.avg_forecast))
print("简单平均法",rms2)

方法三、移动平均法

'''
3、移动平均法：物品价格在一段时间内大幅上涨，但后来又趋于平稳。我们只取最近几个时期的价格平均值。很明显这里的逻辑是只有最近的值最要紧。
这种用某些窗口期计算平均值的预测方法就叫移动平均法。计算移动平均值涉及到一个有时被称为“滑动窗口”的大小值p。使用简单的移动平均模型，
我们可以根据之前数值的固定有限数p的平均值预测某个时序中的下一个值。这样，对于所有的 i>p：y^l=(yi−1+yi−2+...+yi−p)/p.
加权移动平均法:“滑动窗口期”内的值被赋予不同的权重。通常来讲，最近时间点的值发挥的作用更大了。即y^l=1m(w1∗yi−1+w2∗yi−2+...+wm∗yi−m)
这种方法并非选择一个窗口期的值，而是需要一列权重值（相加后为1）。
'''

方法四、简单指数法SES


'''
4、简单指数法SES：在将所有数据考虑在内的同时也能给数据赋予不同的权重。
对于没有明显趋势或季节规律的预测数据，SES是一个很好的选择。
y^T+1=αyT+α(1−α)yT−1+α(1−α)2yTt−2+...
它可以写为：y^T+1=αyT+(1−α)yT−1
所以本质上，我们是用两个权重α和1−α得到一个加权移动平均值，让表达式呈递进形式。
'''
from statsmodels.tsa.api import SimpleExpSmoothing
y_hat_exp_avg=test.copy()
fit=SimpleExpSmoothing(train.Count).fit(smoothing_level=0.6,optimized=False)  #smoothing_level：平滑参数   optimized：是否自动调优
y_hat_exp_avg['SES']=fit.forecast(len(test)) #forecast(n):预测未来的n个点
train.Count.plot(figsize=(16,10),title='SES',fontsize=14)
test.Count.plot(figsize=(16,10),title='SES',fontsize=14)
y_hat_exp_avg.SES.plot(figsize=(16,10),title='SES',fontsize=14)
plt.legend(loc='best')
plt.show()rms3=sqrt(mean_squared_error(test.Count,y_hat_exp_avg.SES))
print("SES",rms3)

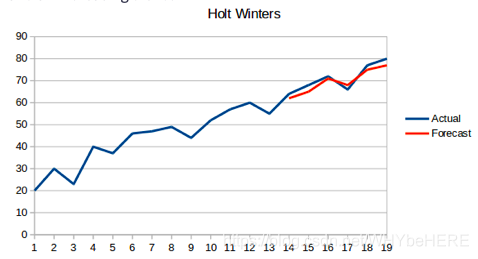
方法五、Holt线性趋势法

当model=‘additive’，即观察值=趋势值+季节性值+残差

当model=‘multiplicative’，即观察值=趋势值x季节性值x残差

'''
5、霍尔特(Holt)线性趋势法:如果物品的价格是不断上涨的，我们上面的方法并没有考虑这种趋势，即我们在一段时间内观察到的价格的总体模式。
每个时序数据集可以分解为相应的几个部分：趋势（Trend），季节性(Seasonal)和残差(Residual)。任何呈现某种趋势的数据集都可以用霍尔特线性趋势法用于预测。
'''
import statsmodels.api as sm
sm.tsa.seasonal_decompose(train.Count).plot()
#所谓分解就是将时序数据分离成不同的成分，分解有：长期趋势Trend、季节性seasonality和随机残差residuals
#statsmodels也支持两类分解模型，加法模型和乘法模型，model的参数设置为"additive"（加法模型）和"multiplicative"（乘法模型）。
#当趋势呈线性增加或下降时，用加法模型，当趋势呈指数级增加或下降时，用乘法模型
result=sm.tsa.stattools.adfuller(train.Count)
#增广Dickey-Fuller检验可用于在序列相关的情况下，对单变量过程中的单位根进行检验。
plt.show()
#发现数据集呈现某种趋势，用holt.该算法包含三个方程：一个水平方程，一个趋势方程，一个方程将二者相加以得到预测值y^
#水平方程显示它是观测值和样本内单步预测值的加权平均数，趋势方程显示它是根据 ℓ(t)−ℓ(t−1) 和之前的预测趋势 b(t−1) 在时间t处的预测趋势的加权平均值。
from statsmodels.tsa.api import Holt
y_hat_holt=test.copy()
fit=Holt(train.Count).fit(smoothing_level=0.3,smoothing_trend=0.1)
y_hat_holt["Holt_linear"]=fit.forecast(len(test))
train.Count.plot(figsize=(16,10),title='Holt_linear',fontsize=14)
test.Count.plot(figsize=(16,10),title='Holt_linear',fontsize=14)
y_hat_holt.Holt_linear.plot(figsize=(16,10),title='Holt_linear',fontsize=14)
plt.legend(loc="best")
plt.show()mse4=sqrt(mean_squared_error(test.Count,y_hat_holt.Holt_linear))
print("Holt_linear:",mse4)

分解数据如下：

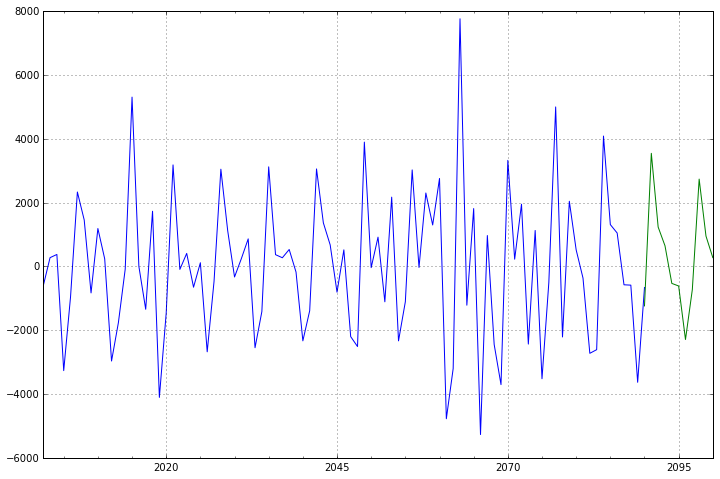
方法六、指数平滑法


'''
6、指数平滑法
如果数据集在一定时间段内的固定区间内呈现相似的模式，那么该数据集就具有季节性。
Holt-Winters季节性预测模型由预测函数和三次平滑函数——一个是水平函数ℓt，一个是趋势函数bt，一个是季节分量 st，以及平滑参数α,β和γ。
季节函数为当前季节指数和去年同一季节的季节性指数之间的加权平均值。
当季节性变化大致相同时，优先选择相加方法，而当季节变化的幅度与各时间段的水平成正比时，优先选择相乘的方法。
'''
from statsmodels.tsa.api import ExponentialSmoothingy_hat_holt_seasonal=test.copy()
fit_seasonal=ExponentialSmoothing(train.Count,trend='add',seasonal_periods=7,seasonal='add').fit()
#seasonal_period = 7作为每周重复的数据
y_hat_holt_seasonal["Holt_Winter"]=fit_seasonal.forecast(len(test))
train.Count.plot(figsize=(16,10),title='Holt_Winter',fontsize=14)
test.Count.plot(figsize=(16,10),title='Holt_Winter',fontsize=14)
y_hat_holt_seasonal.Holt_Winter.plot(figsize=(16,10),title='Holt_Winter',fontsize=14)
plt.legend(loc="best")
plt.show()mse5=sqrt(mean_squared_error(test.Count,y_hat_holt_seasonal.Holt_Winter))
print("mse5:",mse5)

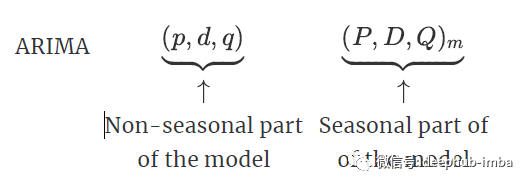
方法七、自回归移动平均模型ARIMA


'''
7、自回归移动平均模型ARIMA
指数平滑模型都是基于数据中的趋势和季节性的描述，而自回归移动平均模型的目标是描述数据中彼此之间的关系。ARIMA的一个优化版就是季节性ARIMA。
'''
y_hat_holt_arima=test.copy()
arima_fit=sm.tsa.statespace.SARIMAX(train.Count,order=(2,1,4),seasonal_order=(0,1,1,7)).fit()#季节性分量  非季节性分量
y_hat_holt_arima["SARIMA"]=arima_fit.forecast(len(test))
train.Count.plot(figsize=(16,10),title='SARIMA',fontsize=14)
test.Count.plot(figsize=(16,10),title='SARIMA',fontsize=14)
y_hat_holt_arima.SARIMA.plot(figsize=(16,10),title='SARIMA',fontsize=14)
plt.legend(loc="best")
plt.show()mse6=sqrt(mean_squared_error(test.Count,y_hat_holt_arima.SARIMA))
print("mse6:",mse6)