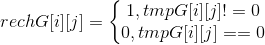文章目录
- 位运算
- 二进制数加法步骤
- 例子
- 代码演示
二进制的加法需要用到位运算,所以先来复习下位运算。
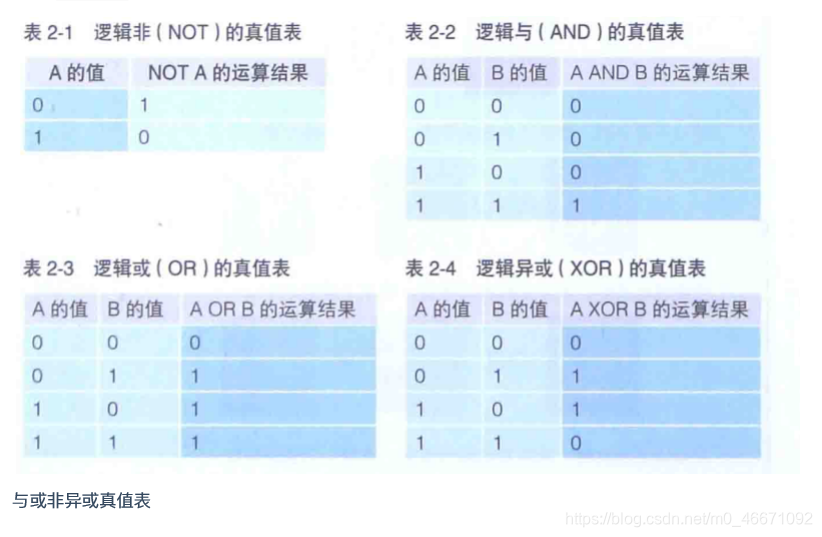
位运算
| 运算 | 符号(java) | 描述 |
|---|---|---|
| 位与 | & | 都为1,结果为1,否则为0。 |
| 位或 | | | 有一个为1或两个位都为1,则结果为1,否则为0。换句话说,只有两个都为0,则结果为0 ,其它为1。 |
| 异或 | ^ | 两个位相同,其为0。两个位不同,其为1。 |
| 取反 | ~ | 0变为1,1变为0。 |
| 左移 | << | 将二进制左移指定位数,右侧补0 |
| 右移 | >> | 将二进制由移指定位数,右侧超出部分截取丢弃。如a>>b相当于a/2^b。 |
二进制数加法步骤
- 将两二进制数异或,获取无需进位的二进制数
- 将两二进制数位与,获取需进位的二进制数
- 将2步骤的进位二进制数左移1位,得到进位之后的二进制数
- 将3步骤的已进位的二进制数与1步骤的不需进位的二进制数位与,如果位与的结果等于0,即表示无进位需处理了,进入步骤4。如果结果不为0,则表明还有进位需要处理,则继续重复1、2、3、4步骤。
- 将1、2步骤的结果进行位或,其所得结果即为加法之后的二进制数。
例子
如,二进制数0100(4)与1110(14)相加得二进制结果10010(18),其步骤如下:

代码演示
python.
def add(a, b):ncb = a ^ b # 不需要进位的二进制数部分cb = (a & b) << 1 # 进位的二进制数部分if ncb & cb != 0: # 如果位与之后的结果还有1,则表示还有需要进位的return add(ncb, cb) # 递归return ncb | cb # 进位与不进位的二进制取位或得到结果if __name__ == '__main__':print(add(0, 3))