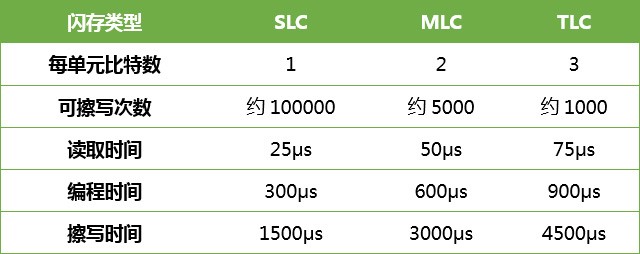
图如下:
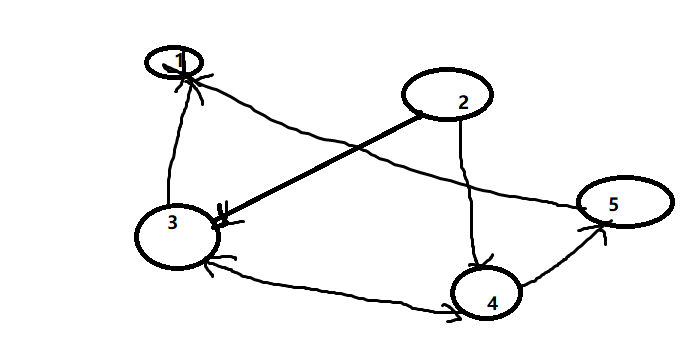
package com;public class Main {public static void main(String[] args) {// 邻接矩阵int adjacency[][] = { { 0, 0, 0, 0, 0 }, { 0, 0, 1, 1, 0 }, { 1, 0, 0, 1, 0 }, { 0, 0, 1, 0, 1 },{ 1, 0, 0, 0, 0 } };// 可达矩阵int reachability[][] = null;System.out.println("邻接矩阵:");show(adjacency);reachability = addUnit(adjacency);show(reachability);int n = 0;do {n++;reachability = square(reachability);reachability = format(reachability);System.out.println("第" + n + "次布尔运算");show(reachability);} while (!equals(reachability, format(square(reachability))));System.out.println("可达矩阵:");show(reachability);}// 矩阵+单位矩阵public static int[][] addUnit(int primitive[][]) {int[][] result = new int[primitive.length][primitive.length];for (int x = 0; x < primitive.length; x++) {for (int y = 0; y < primitive[x].length; y++) {result[x][y] = primitive[x][y];}}for (int i = 0; i < result.length; i++) {for (int j = 0; j < result[i].length; j++) {if (i == j) {result[i][j] = 1;}}}return result;}// 打印矩阵public static void show(int matrix[][]) {for (int i = 0; i < matrix.length; i++) {for (int j = 0; j < matrix[i].length; j++) {System.out.print(matrix[i][j] + ",");}System.out.println();}System.out.println();}// 矩阵是否相等public static boolean equals(int a[][], int b[][]) {if (a.length != b.length) {// 行数是否相等return false;} else {for (int i = 0; i < a.length; i++) {if (a[i].length != b[i].length) {// i行列数是否相等return false;} else {for (int j = 0; j < a[i].length; j++) {if (a[i][j] != b[i][j]) {// i行j列的数值是否相等return false;}}}}}return true;}// 矩阵自乘public static int[][] square(int primitive[][]) {int[][] result = new int[primitive.length][primitive.length];int[][] list = new int[primitive.length][primitive.length];for (int x = 0; x < primitive.length; x++) {for (int y = 0; y < primitive[x].length; y++) {result[x][y] = primitive[x][y];}}int temp;for (int i = 0; i < result.length; i++) {for (int n = 0; n < result[i].length; n++) {temp = 0;for (int j = 0; j < result[i].length; j++) {temp += result[i][j] * result[j][n];}list[i][n] = temp;}}return list;}// 格式化public static int[][] format(int primitive[][]) {int[][] result = new int[primitive.length][primitive.length];for (int x = 0; x < primitive.length; x++) {for (int y = 0; y < primitive[x].length; y++) {result[x][y] = primitive[x][y];}}for (int i = 0; i < result.length; i++) {for (int j = 0; j < result[i].length; j++) {if (result[i][j] > 0) {result[i][j] = 1;}}}return result;}}
// 输出邻接矩阵:
0,0,0,0,0,
0,0,1,1,0,
1,0,0,1,0,
0,0,1,0,1,
1,0,0,0,0,1,0,0,0,0,
0,1,1,1,0,
1,0,1,1,0,
0,0,1,1,1,
1,0,0,0,1,第1次布尔运算
1,0,0,0,0,
1,1,1,1,1,
1,0,1,1,1,
1,0,1,1,1,
1,0,0,0,1,可达矩阵:
1,0,0,0,0,
1,1,1,1,1,
1,0,1,1,1,
1,0,1,1,1,
1,0,0,0,1,










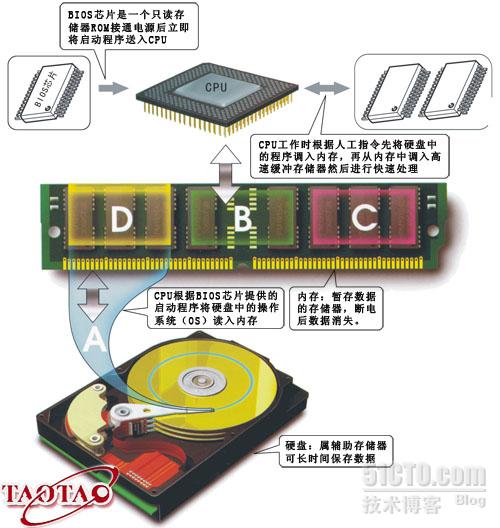


![[硬件] 简单介绍磁盘结构及工作原理](https://img-blog.csdnimg.cn/img_convert/e699e6d14ca2b71c066dd5e00d65e9de.png)