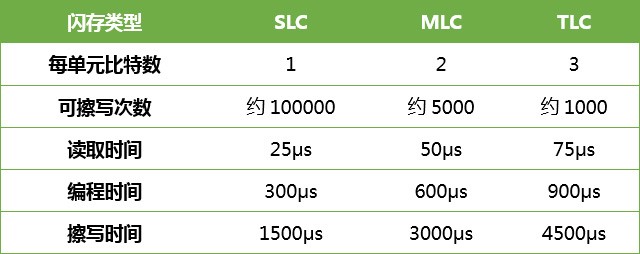
我们根据有向图的连通情况,可以将图分成四种类型
- 非连通图
- 弱连通图
- 单向连通图
- 强连通图
我们可以通过邻接矩阵A,计算可达矩阵B,然后经过二值化之后得到可达性矩阵P来判断该图属于以上哪一种。
- 如果P中元素都为1,说明任意两点之间都可达,那么这是一个强连通图;
- 如果 P ′ = P ∪ P T P' = P \cup P^T P′=P∪PT除对角线之外全为1,说明任意两个点之间存在可达通路,那么这是一个单向连通图;
- 如果 A ′ = A ∪ A T A' = A \cup A^T A′=A∪AT作为邻接矩阵,然后求得可达矩阵所有元素为1,那么这个图为弱连通图。
我们通过程序来判断一下下面这个图的连通性:

import numpy as npA = np.matrix([[0,1,0,1],[0,0,1,0],[0,0,0,1],[0,0,0,0]])def get_accessible(A):B = Aitem = Afor i in range(len(A)):item = np.matmul(item,A)B = B + itemreturn BB = get_accessible(A)
P = np.array(B, dtype= bool)
Pt = P.transpose()
Pp = P + Ptprint("强连通矩阵判据")
print(P)
print("单向连通矩阵判据")
print(Pp)A = A + A.transpose()
B = get_accessible(A)
P = np.array(B, dtype= bool)
print("弱连通矩阵判据")
print(P)

可见,该图的矩阵表示满足弱联通和单向连通矩阵判据,所以是一个单向连通矩阵。






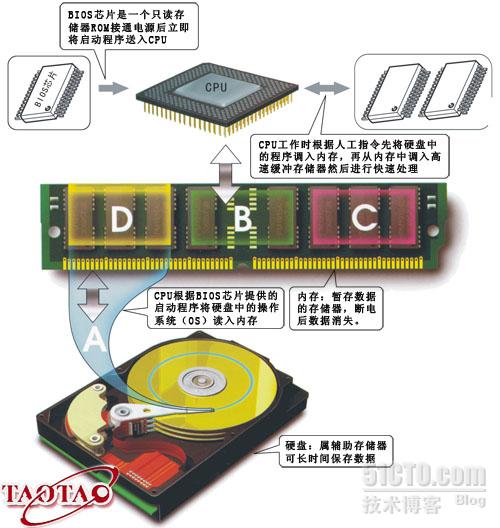


![[硬件] 简单介绍磁盘结构及工作原理](https://img-blog.csdnimg.cn/img_convert/e699e6d14ca2b71c066dd5e00d65e9de.png)