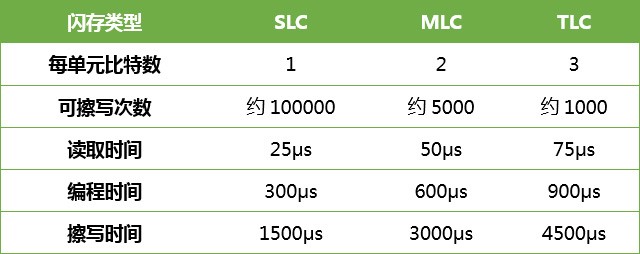
一、介绍概念
1、邻接矩阵
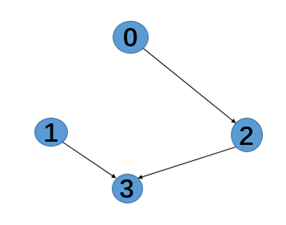
将一个n个节点的图,转化成一个n*n的矩阵G,G[i][j]表示第i个节点到第j个节点的的权重。

对于上图邻接矩阵为:

2、度
度分为入度和出度:某个节点的入度就是可以通过一条边到达这个节点的节点个数,某个节点的出度就是可以通过一条边到达其它节点的节点个数

在这个图中只有3节点可以到达0节点,0节点可以到达1节点和2节点,所以0节点的入度为:1,出度为2
3、可达矩阵:
可达矩阵是一个n*n的矩阵rechG,如果节点i可以到达节点j,那么rechG[i][j]=1,反之,则为rechG[i][j]=0;可以采取这种计算方式:
4、连通(有向图)
(1)强连通:当每个节点都可以到达其它节点的时候就是强连通
如图:(下图就是一个强连通图)

(2)单向连通:只要对任意两个节点:节点i, 节点j,如果i可以到达j(条件1),或者j可以到达i(条件2),只要满足一个条件,就是单向连通图。
如果:(下图是一个单向连通图)
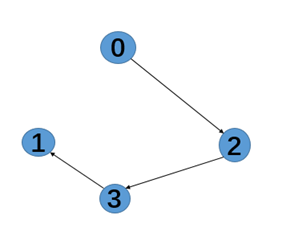
(3)弱连通:将有向图转化成无向图的时候,如果这个无向图是强连通,那么原图是弱连通。
结论:单向连通图一定是弱通图,弱连通图不一定是单向连通图
如下图:是弱连通图,单不是单向连通图
二、实现思路(邻接矩阵)
1、出度和入度
出度:邻接矩阵第i行的和(主对角线为0)就是第i个节点的出度
入度:邻接矩阵第j列的和(主对角线为0)就是第j个节点的入度
如下是代码:graphic[i][j]是邻接矩阵:
/*输出有序顶点对,以及每个顶点的入度和出度*/
void display_degree()
{
cout << "\n每个顶点的入度和出度如下:" << endl;
for (int i = 0; i < vernum; i++)
{
cout << "第" << i << "个顶点的入度和出度:";
int intoDegree = 0; //入度
int outDegree = 0; //出度
for (int j = 0; j < vernum; j++)
{
if (graphic[j][i] != 0&&i!=j)
intoDegree++;
if (graphic[i][j] != 0&&i!=j)
outDegree++;
}
cout << intoDegree << "\t" << outDegree << endl;
}
}
2、可达矩阵:
可达矩阵计算方式很多,下面给出其中一种解法:rechG是计算的可达矩阵
代码如下:
/*矩阵乘法*/
void matrix_multi(int A[][MAX],int B[][MAX])
{
//乘法的最后结果保存再A矩阵中
int result[MAX][MAX];
memset(result, 0, sizeof(result));
for (int i = 0; i < vernum; i++)
{
for (int j = 0; j < vernum; j++)
{
for (int v = 0; v < vernum; v++)
{
result[i][j] += A[i][v] * B[v][j];
}
}
}
//拷贝到A中
for (int i = 0; i < vernum; i++)
{
for (int j = 0; j < vernum; j++)
{
A[i][j] = result[i][j];
}
}
}
/*求可达矩阵*/
void rechable_matrix()
{
int tmp_matrix[MAX][MAX]; //可到达矩阵的每一项比如A^i
for (int i = 0; i < vernum; i++) //主对角线设置为1
graphic[i][i] = 1;
for (int i = 0; i < vernum; i++)
{
for (int j = 0; j < vernum; j++)
{
tmp_matrix[i][j] = graphic[i][j];
rech_matrix[i][j] = graphic[i][j];
}
}
for (int i = 1; i < vernum; i++)
{
for (int j = 0; j < i; j++)
{
matrix_multi(tmp_matrix, graphic);
}
//相加
for (int m = 0; m < vernum; m++)
{
for (int n = 0; n < vernum; n++)
{
rech_matrix[m][n] = rech_matrix[m][n] + tmp_matrix[m][n];
}
}
}
cout << "可达矩阵为:" << endl;
for (int i = 0; i < vernum; i++)
{
for (int j = 0; j < vernum; j++)
{
if (rech_matrix[i][j] != 0)
cout << "1" << "\t";
else
cout << "0" << "\t";
}
cout << endl;
}
}
3、判断图的连通性
强连通:通过上面计算的可达矩阵,如果所有元素都不为0,就是强连通
单向连通图:如果已经判断不为强连通,计算对于所有i,j的rech_matrix[i][j]不为0(条件1)和rech_matrix[j][i]不为0(条件2),如果条件1和条件2满足其中一个条件,就是单向连通图。
弱连通图:如果不是强连通图,将有向图变成无向图,如果无向图是强连通,那么有向图是弱连通。
三、代码如下
// graphics_judge.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//#include <iostream>
using namespace std;
#define MAX 100//邻接矩阵的变量
int vernum; //节点个数
int graphic[MAX][MAX];
int rech_matrix[MAX][MAX]; //可达矩阵/*初始化矩阵*/
void init_graphic();
/*输出有序顶点对,以及每个顶点的入度和出度*/
void display_degree();
/*矩阵乘法*/
void matrix_multi(int A[][MAX], int B[][MAX]);
/*求可达矩阵*/
void rechable_matrix();
/*判断强连通或则若连通:通过可达矩阵判断,强连通返回0,单向连通返回1,否则返回-1*/
int judge_connected_graph();
/*判断是否是弱连通*/
void judge_connected_weakgraph();int main()
{init_graphic();display_degree();rechable_matrix();int flag = judge_connected_graph();if (flag == 0){cout << "输入的图是强连通图" << endl;}else{if (flag == 1)cout << "输入的图是单向连通图" << endl;judge_connected_weakgraph();}return 0;
}/*初始化矩阵*/
void init_graphic()
{cout << "请输入图的节点个数:";cin >> vernum;cout << "请输入一个为" << vernum << "的0,1方正:" << endl;for (int i = 0; i < vernum; i++){for (int j = 0; j < vernum; j++){cin >> graphic[i][j];if (i == j)graphic[i][j] = 1;}}
}/*输出有序顶点对,以及每个顶点的入度和出度*/
void display_degree()
{cout << "输出有序顶点对:" << endl;for (int i = 0; i < vernum; i++){for (int j = 0; j < vernum; j++){if (graphic[i][j] != 0){cout << "<" << i << "," << j << ">" << "\t";}}}cout << "\n每个顶点的入度和出度如下:" << endl;for (int i = 0; i < vernum; i++){cout << "第" << i << "个顶点的入度和出度:";int intoDegree = 0; //入度int outDegree = 0; //出度for (int j = 0; j < vernum; j++){if (graphic[j][i] != 0&&i!=j)intoDegree++; if (graphic[i][j] != 0&&i!=j)outDegree++;}cout << intoDegree << "\t" << outDegree << endl;}
}/*矩阵乘法*/
void matrix_multi(int A[][MAX],int B[][MAX])
{//乘法的最后结果保存再A矩阵中int result[MAX][MAX];memset(result, 0, sizeof(result));for (int i = 0; i < vernum; i++){for (int j = 0; j < vernum; j++){for (int v = 0; v < vernum; v++){result[i][j] += A[i][v] * B[v][j];}}}//拷贝到A中for (int i = 0; i < vernum; i++){for (int j = 0; j < vernum; j++){A[i][j] = result[i][j];}}}/*求可达矩阵*/
void rechable_matrix()
{int tmp_matrix[MAX][MAX]; //可到达矩阵的每一项比如A^ifor (int i = 0; i < vernum; i++) //主对角线设置为1graphic[i][i] = 1;for (int i = 0; i < vernum; i++){for (int j = 0; j < vernum; j++){tmp_matrix[i][j] = graphic[i][j];rech_matrix[i][j] = graphic[i][j];}}for (int i = 1; i < vernum; i++){for (int j = 0; j < i; j++){matrix_multi(tmp_matrix, graphic);}//相加for (int m = 0; m < vernum; m++){for (int n = 0; n < vernum; n++){rech_matrix[m][n] = rech_matrix[m][n] + tmp_matrix[m][n];}}}cout << "可达矩阵为:" << endl;for (int i = 0; i < vernum; i++){for (int j = 0; j < vernum; j++){if (rech_matrix[i][j] != 0)cout << "1" << "\t";elsecout << "0" << "\t";}cout << endl;}
}int judge_connected_graph()
{int flag_connected = 0; //强连通为0,单向连通为1,否则为-1/*判断强连通和单向连通*/for (int i = 0; i < vernum; i++){for (int j = 0; j < vernum; j++){if (rech_matrix[i][j] == 0)flag_connected = 1;}}if (flag_connected == 0)return 0;for (int i = 0; i < vernum; i++){for (int j = 0; j < vernum; j++){if (rech_matrix[i][j] == 0 && rech_matrix[j][i] == 0)return -1;}}return 1;
}/*判断是否是弱连通*/
void judge_connected_weakgraph()
{for (int i = 0; i < vernum; i++){for (int j = 0; j < vernum; j++){if (graphic[i][j] != 0){graphic[j][i] = graphic[i][j];}}}cout << "转化成无向图后的可达矩阵为:" << endl;rechable_matrix();if (judge_connected_graph() == 0)cout << "可以发现原图是个弱连通图" << endl;elsecout << "可以发现原图不是一个弱连通图" << endl;
}
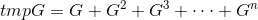
![rechG[i][j]=\left\{\begin{matrix} 1, tmpG[i][j]!=0 & \\ 0, tmpG[i][j]==0& \end{matrix}\right.](https://img-blog.csdnimg.cn/20181221204127357)






![[硬件] 简单介绍磁盘结构及工作原理](https://img-blog.csdnimg.cn/img_convert/e699e6d14ca2b71c066dd5e00d65e9de.png)