有限马尔科夫链状态分解+Kosaraju 算法
- 1 实验内容
- 2 理论基础
- 3 题目分析
- 4 按常返性和互通性对状态空间进行分解算法流程
- 4.1 强连通性和强连通分量
- 4.2 基于有向图 Kosaraju 算法的有限马尔科夫链状态分解
- 4.3 算法正确性证明
- 4.4 算法复杂度分析
- 5 按周期对不可约闭集进行分解
- 6 对例题分解验证算法正确性
- 7 代码使用
- 8 总结
1 实验内容
生成有 100 个状态的齐次马尔科夫链,状态转移矩阵随机生成(在满足完备
性约束下,可以随机由代码设置,注意保证状态有一定比例与其他状态的联通,
比如 3%;也可以自己提前设置好,但要保证有 2 个以上不可约子集)。
- 将状态空间按常返性和互通性进行分解;
- 在 1 的基础上对周期不可约马尔可夫链进行分解。
2 理论基础
设 C C C 为状态空间 I 的非空子集,若对任意 i ∈ C & & j ∉ C i\in C \&\& j \notin C i∈C&&j∈/C 都有 p i j = 0 p_{ij}=0 pij=0,则称为 C C C (随机)闭集,若 C C C 中所有状态是互通的,称 C C C 是不可约的闭集。若马尔可夫链 { X n } \{X_n\} {Xn} 的状态空间 I I I 是不可约的闭集,则称 { X n } \{X_n\} {Xn} 为不可约的马尔可夫链。
-
按常返性和互通性进行状态空间的分解
任一马尔可夫链的状态空间 I,可唯一地分解成有限个或可列个不相交的集 D , C 1 , C 2 , . . . D, C_1, C_2, ... D,C1,C2,... 之和,使得:
- 每一 C n , n = 1 , 2 , . . . C_n,\ n=1, 2, ... Cn, n=1,2,... 是常返态组成的不可约闭集;
- C n , n = 1 , 2 , . . . C_n,\ n=1, 2, ... Cn, n=1,2,... 中的状态同类,即或全是正常返,或全是零常返,它们有相同的周期,且 f j k = 1 , j , k ∈ C n f_{jk}=1,\ j,k \in C_n fjk=1, j,k∈Cn ;
- D D D 是由全体非常返状态组成,自 𝐶 n 𝐶_n Cn 中的状态不能到达 D D D 中的状态。
-
按对周期不可约马尔可夫链进行分解
周期为 d d d 的不可约马氏链,其状态空间 C C C 可唯一地分解为$ d $个互不相交的子集之和,即:
C = ∪ r = 0 d − 1 G r , G r ∩ G s = Φ , r ≠ s C=\cup_{r=0}^{d-1}G_r,\quad G_r \cap G_s = \Phi, \quad r \ne s C=∪r=0d−1Gr,Gr∩Gs=Φ,r=s
且使自 𝐺 r 𝐺_r Gr中任一状态出发,经一步必转移进入 𝐺 r + 1 𝐺_{r+1} Gr+1 中(其中 G d = G 0 G_d = G_0 Gd=G0 )。
3 题目分析
由理论分析中的分解定理可知,对于有限马尔科夫链而言,状态常反与否及按周期的分解均与转移矩阵 P = ( p i j ) P=(p_{ij}) P=(pij) 的具体取值无关,而仅仅取决于各 p i j p_{ij} pij 是否为零。
由此可知,对于有限马尔科夫链的状态分解,我们只需要考虑转移矩阵 P = ( p i j ) P=(p_{ij}) P=(pij) 相应的邻接矩阵 B = ( b i j ) B=(b_{ij}) B=(bij) ,其中:
B i j = { 0 , p i j = 0 1 , p i j ≠ 0 i , j = 0 , 1 , 2 , . . . , n − 1 B_{ij}=\begin{cases} 0, \quad p_{ij} = 0\\ 1, \quad p_{ij} \ne 0 \end{cases} \quad i,j=0,1,2,...,n-1 Bij={0,pij=01,pij=0i,j=0,1,2,...,n−1
当且仅当 b i j = 1 b_{ij}=1 bij=1 时,表示状态 𝑖 𝑖 i 可一步到达状态 𝑗 𝑗 j。
我们可以看到,若状态 𝑖 𝑖 i 可到达状态 𝑗 𝑗 j,则存在长度至多为 n − 1 n-1 n−1 的路径从 𝑖 𝑖 i 到达 j j j。因而为求各节点的闭包,只需要计算 B B B 的可达矩阵 B ‾ \overline{B} B:
B ‾ = B + B 2 + ⋯ + B n \overline{B} =B+B^2+\cdots + B^n B=B+B2+⋯+Bn
其中乘法、加法均为布尔运算, B ‾ \overline{B} B 的第 𝑖 , 𝑗 𝑖, 𝑗 i,j项 b i j ‾ = 1 \overline{b_{ij}} = 1 bij=1 表示自 𝑖 𝑖 i 出发必可在有限步到达 𝑗 𝑗 j; b i j ‾ = 0 \overline{b_{ij}} = 0 bij=0 表示永远不可能达到 𝑗 𝑗 j。
通过以上分析可知,相对于直接计算 n n n 步转移矩阵来判断可达,转化为可达矩阵的布尔运算大大减少了计算量。可以将其转为一个有向图算法。
4 按常返性和互通性对状态空间进行分解算法流程
4.1 强连通性和强连通分量
有向图中的强连通性是一种顶点之间等价关系,它有着以下性质:
- 自反性:任意顶点 v 和自己都是强连通的。
- 对称性:如果 v 和 w 是强连通的,那么 w 和 v 也是强连通的。
- 传递性:如果 v 和 w 是强连通的且 w 和 x 也是强连通的,那么 v 和 x 也是强连通的。
作为一种等价关系,强连通性将所有顶点分为了一些等价类,每个等价类都是由相互均为强连通的顶点的最大子集组成的。我们将这些子集称为强连通分量,请见图 1。样图含有 5 个强连通分量。

4.2 基于有向图 Kosaraju 算法的有限马尔科夫链状态分解
- 读入转移矩阵,生成有向图 G G G(若 p i j ≠ 0 p_{ij}\ne 0 pij=0,则有一条从 𝑖 𝑖 i 指向 𝑗 𝑗 j 的边)。
- 利用 Kosaraju 算法得到有向图 G G G 中所有的强连通分量。
- 遍历每个强连通分量,若一个强连通分量中的节点不能达到另一个强连通分量,说明此强连通分量是一个不可约的闭集 𝐶 𝐶 C;若可以达到另一个强连通分量,则说明此分量中的节点是非常反的,属于子集 D D D
- 验证算法正确性。
4.3 算法正确性证明
- 所有的强连通分量满足分量中的节点相互连通(对于马尔科夫链而言,就是状态可达),并且不会和其他强连通分量中的节点相互连通。现用反证法证明如下:若强连通分量 C 1 C_1 C1 中的节点 i i i 与另一强连通分量 C 2 C_2 C2 中的节点 j j j 相互可达,是强连通的,那么对于 C 1 C_1 C1 中的其他节点 k k k 均可通过 i i i 到达 j j j , j j j 也可以通过 i i i 到达 k k k ,那么明 𝑗 , 𝑘 𝑗, 𝑘 j,k 是强连通的,按照有向图强连通分量的定义, 𝑗 𝑗 j 也将属于 C 1 C_1 C1 ,而本身 j j j 不属于 C 1 C_1 C1 ,所以说明,若 C 1 C_1 C1 一个最大不可约的。
- 若强连通分量中的节点不能到达另一个强连通分量,那么此分量是一个闭集,通过 4.2 算法的第三步可以找出所有的闭集,剩余的强连通分量必然是由非常反的状态(节点),用反证法证明:若剩余的强连通分量(即可从本强连通分量到另一个强连通分量)中的节点(状态) 𝑖 𝑖 i是常反的,那么从 𝑖 𝑖 i能通过 𝑖 𝑖 i所在的强连通分量到达其余强连通分量 𝑗 𝑗 j,然后再回到 𝑖 𝑖 i,那么说明 𝑖 → 𝑗 → 𝑖 𝑖→𝑗→𝑖 i→j→i,那也可 𝑖 → 𝑗 → 𝑖 → 𝑗 𝑖→𝑗→𝑖→𝑗 i→j→i→j,那么说明 𝑖 𝑖 i, 在同一强连通分量中,然而 Kosaraju算法保证 𝑖 , 𝑗 𝑖, 𝑗 i,j不在同一强连通分量中,与假设矛盾,所以剩余的强连通分量中的节点都是非常反的,属于集合𝐷。
- 在算法第三步中不可达到外部的强连通分量是否是周期相同的?由上两步分析可知,不可达到外部的强连通分量是一个不可约闭集,因为强连通分量的状态是相互连通的,周期必然相等。
由以上两个证明,可以得知,通过这种方法能成功对有限马尔科夫链进行状态分解。
4.4 算法复杂度分析
假设有限图节点(状态)数量为𝑉,有向边数量为𝐸,算法复杂度分析分为两个部分:
- Kosaraju 算法的复杂度为 𝑂 ( V + E ) 𝑂(V+E) O(V+E)。
- 4.2 算法流程的第三步,也是遍历一次所有的边和节点,所以复杂度也是 𝑂 ( V + E ) 𝑂(V+E) O(V+E)。
综上,整个算法的复杂度为 𝑂 ( V + E ) 𝑂(V+E) O(V+E)。
5 按周期对不可约闭集进行分解
- 选取不可约闭集 C i C_i Ci的某一状态 𝑝 𝑝 p,记其为集合 𝐺 1 𝐺1 G1;
- 由邻接矩阵得到 𝐺 1 𝐺1 G1 中每一状态的所有下一步可达状态,将其全体记为集合 𝐺 2 𝐺2 G2,将 𝐺 2 𝐺2 G2 输出保存得到 𝐶 𝑖 𝐶_𝑖 Ci周期性分解的子集之一 𝐺 j 𝐺_j Gj ;
- 将第二步所得 𝐺 2 𝐺2 G2 记为当前的 𝐺 1 𝐺1 G1,循环第二步操作直至所有状态都归于某一 𝐺 j , j = 1 , 2 , ⋯ , r 𝐺_j,\quad j=1,2,\cdots, r Gj,j=1,2,⋯,r。
由上述步骤,可将某不可约闭集 C i C_i Ci分按周期分解为互不相交子集之并:
C i = ∑ j = 1 r G i C_i=\sum_{j=1}^r G_i Ci=j=1∑rGi
6 对例题分解验证算法正确性
例:设不可约马氏链的状态空间为 C = 1 , 2 , 3 , 4 , 5 , 6 C={1, 2, 3, 4, 5, 6} C=1,2,3,4,5,6,转移矩阵为

状态转移有向图为:

为了能有按常返性和互通性进行状态空间的分解的功能,我加上了第七个状态,此状态能达到 2,3,4 状态。算法输出结果如下图:

然后按周期对不可约马尔科夫链进行状态分解,结果如下:

由实验结果可知,本次设计满足要求。
7 代码使用
只需在 main 函数中修改常量 N 和 ratio 的值即可修改代码,原始的代码是例题的解决,作为一个测试,测试代码的正确性。如需使用随机生成的数据,请将下图的中的第一行注释,第二三行取消注释。

8 总结
具体代码大家可以下载,需要积分,因为我觉得通过上面的分析,自己写也是可行的,希望参考这篇文章的同学们先自己实现。
【有限马尔科夫链状态分解+Kosaraju 算法】代码下载






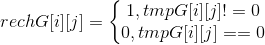




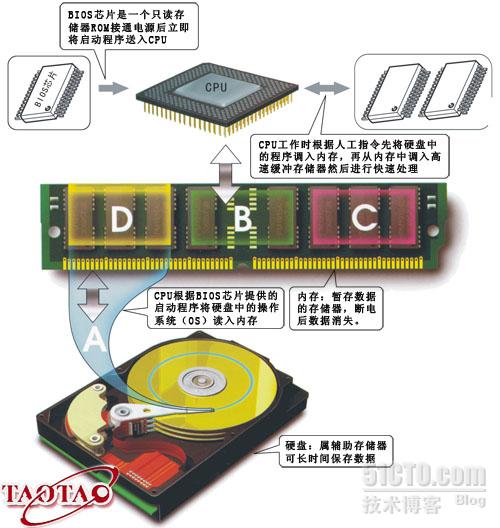


![[硬件] 简单介绍磁盘结构及工作原理](https://img-blog.csdnimg.cn/img_convert/e699e6d14ca2b71c066dd5e00d65e9de.png)