---

第一章 基础算法（一）

---

• 上课的主要任务是把算法的主要思想给理解清楚（虽然讲课的内容和英语差不多，都是以背为主，但是如果不理解算法的话，还是很难应用它的）.
  • 所以我们需要对算法思想，和它为什么是对的，有一个深刻的理解.
• 课后可以做两方面的事情：
  1. 理解算法，并把模板背过（这里的背过不是一个字母一个字母地去背，而是在需要使用该算法时，能够快速地把算法的模板默写出来、调试通过就可以了）；
     • 背也是有方法的，主要是完全熟悉算法思想，结合模板来理解.
     • 默写也是需要找相应的模板题来默写.
  2. 课后刷题.

Q：如何提高算法模板的熟练度？

A：一道模板题写完后，删掉原来的代码重新写一遍，大概重复 $3\sim 5$ 次，就可以对模板有一个很好的记忆了.

---

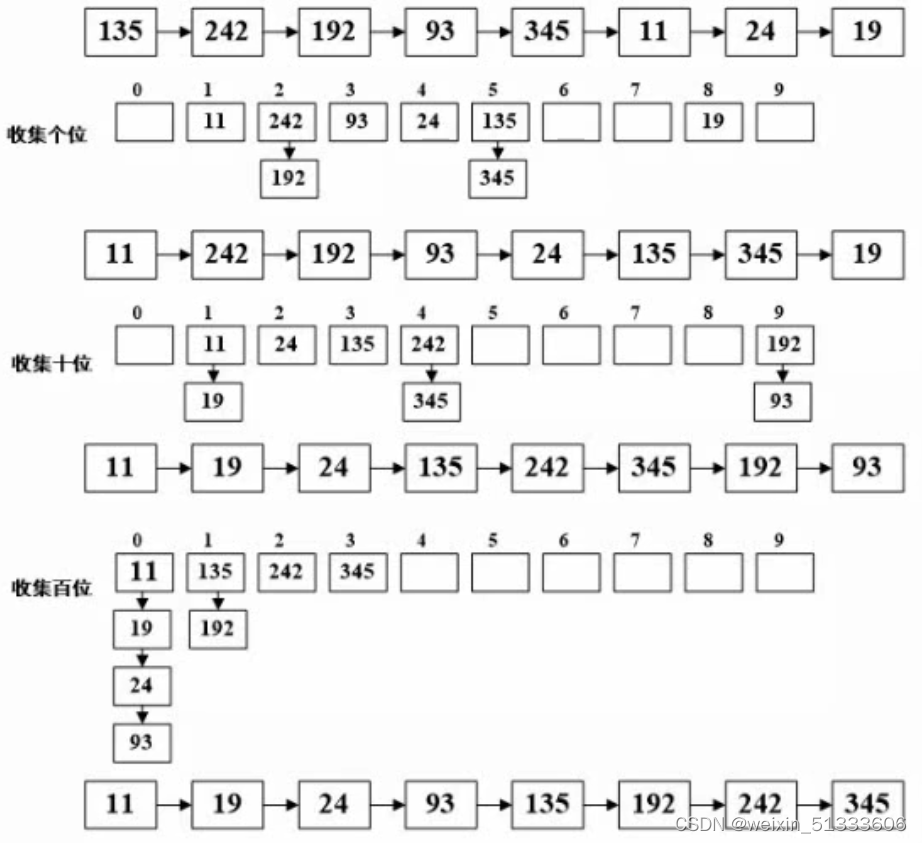
排序

---

• 主要讲两个排序算法（因为其他排序算法在算法竞赛中的应用也不是很多.
• $排序\{\begin{array}{l}快速排序\\ 归并排序\end{array}$.

AcWing 785. 快速排序

原题链接

给定你一个长度为 $n$ 的整数数列。

请你使用快速排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式

输入共两行，第一行包含整数 $n$。

第二行包含 $n$ 个整数（所有整数均在 $1\sim 10^9$ 范围内），表示整个数列。

输出格式

输出共一行，包含 $n$ 个整数，表示排好序的数列。

数据范围

$1\le n\le 100000$

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

时/空限制： 2s / 64MB
来源： 模板题
算法标签：快速排序

yxc’s Solution

• 快速排序的主要思想是分治.

• 对于一段待排序的数组 $\mathrm{q}[\mathrm{L}\sim \mathrm{R}]$ 来说，快速排序的算法流程如下：

  1. 先随便在数组当中找到一个值 $x$ 作为分界点（确定分界点），常用的分界点有如下几种：

     • 取左边界，即 $x=\mathrm{q}[\mathrm{L}]$；

     • 取中间值，即 $x=\mathrm{q}[\mathrm{m}\mathrm{i}\mathrm{d}]$，其中 $\mathrm{m}\mathrm{i}\mathrm{d}=\lfloor \frac{\mathrm{L}+\mathrm{R}}{2}\rfloor$；

     • 取右边界，即 $x=\mathrm{q}[\mathrm{R}]$；

     • 在区间 $[\mathrm{L},\mathrm{R}]$ 中随机一个位置.

       这里推荐使用取中间值作为分界点.

  2. 根据 $x$ 的值，将整个区间分为两半（调整区间）：

     • 将 $⩽x$ 的数放到区间的左半部分，将 $⩾x$ 的数放到区间的右半部分.
     • 注意左半部分和右半部分不一定含有相同数量的数，这是依据 $x$ 的值而定的.
     • 而且 $x$ 不一定是左半部分的最后一个数或右半部分的第一个数（因为可能有很多数和 $x$ 相等），只要符合调整区间的结果就可以.

  3. 递归处理左半部分和右半部分.

     • 因为左半部分的最大值是小于右半部分的最小值的；
     • 如果左半部分和右半部分都分别排好序了，拼接到一起一定是整个数组排好序了的状态.

• 如何优雅地调整区间是快速排序的重难点，有很多种实现方法，这里介绍一种思想比较简单的实现方法：

  1. 先开两个额外的数组 $\mathrm{a}[],\mathrm{b}[]$.
  2. 扫描遍历 $\mathrm{q}[\mathrm{L}\sim \mathrm{R}]$，对于数组 $\mathrm{q}[]$ 的第 $i$ 个数 $\mathrm{q}[\mathrm{i}]$，如果：
     • $\mathrm{q}[\mathrm{i}]⩽x$，将 $\mathrm{q}[\mathrm{i}]$ 插入到数组 $\mathrm{a}[]$ 的末尾.
     • $\mathrm{q}[\mathrm{i}]⩾x$，将 $\mathrm{q}[\mathrm{i}]$ 插入到数组 $\mathrm{b}[]$ 的末尾.
  3. 先将 $\mathrm{a}[]$ 中的数覆盖到 $\mathrm{q}[]$ 中，再将 $\mathrm{b}[]$ 中的数覆盖到 $\mathrm{q}[]$ 中.

• 但是这样会开辟额外的空间，这里介绍一种优美的实现这种思想的方法，不需要开辟额外的空间：

  1. 使用两个指针 $i,j$，第一个指针 $i$ 指向数组开头 $\mathrm{q}[\mathrm{L}]$，第二个指针 $j$ 指向数组结尾 $\mathrm{q}[\mathrm{R}]$.
  2. 指针 $i$ 先往右移动，直到出现 $\mathrm{q}[i]⩾x$ 时 $i$ 停止移动；指针 $j$ 再往左移动，直到出现 $\mathrm{q}[j]⩽x$ 时停止移动.
  3. 此时 $\mathrm{q}[i]$ 需要放到右半部分，而 $\mathrm{q}[j]$ 需要放到左半部分，因此只需要交换它们就好了.
     • 交换完后，有 $\mathrm{q}[\mathrm{L}\sim i]$ 都是左半部分的数，$\mathrm{q}[j\sim \mathrm{R}]$ 都是右半部分的数.
     • 即在任何时刻，$i$ 左边的数都是 $⩽x$ 的， $j$ 右边的数都是 $⩾x$ 的.
  4. 直到 $i$ 和 $j$ 相遇或越过彼此为止.

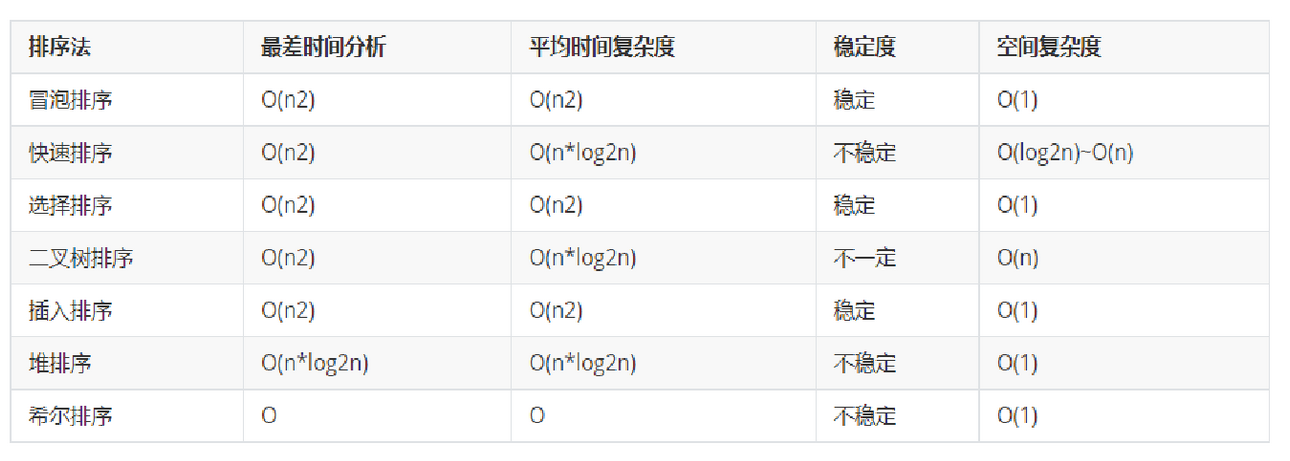
• 快速排序是不稳定的排序算法，期望时间复杂度为 $O(n\log n)$.

  快速排序的最坏时间复杂度为 $O(n^2)$.

  但是它期望每次都能将数组对半分，那么递归过程就类似一棵二叉树，其递归层数为 $\log n$，故期望的时间复杂度为 $O(n\log n)$.

  这里的稳定与不稳定不是指排序算法的时间效率，而是两个相同的数字，在排序前后的位置是不是相对不变的.

  如果位置一定相对不变，则称排序算法是稳定的；否则，排序算法就是不稳定的.

  当然，快速排序是可以变成稳定的排序算法，比如用某种机制让所有的数字不相同.

#include <cstdio>
#include <algorithm>using namespace std;const int N = 1e5 + 10;int n;
int q[N];void quick_sort(int q[], int L, int R)
{if (L >= R) return;int x = q[(L + R) / 2], i = L - 1, j = R + 1;/*由于下面的 while 循环的逻辑是先将指针往中间移动一次，再判断其是左半部分的数还是右半部分的数，所以这里指针的初始值是左右边界往外再扩一格.*/while (i < j){do i ++ ; while (q[i] < x);do j -- ; while (q[j] > x);if (i < j) swap(q[i], q[j]);}quick_sort(q, L, j);quick_sort(q, j + 1, R);/*这里最终可能会出现 i = j 或者 i = j + 1 两种情况，综合考虑，如上 while 循环能保证 L ~ i - 1 在左半部分， j + 1 ~ R 在右半部分，这里取 j + 1 ~ R 为右半部分，则 L ~ j 即为左半部分，但需要注意这种写法不能去分界点为 q[R]，因为可能会出现 j = R 而出现死循环.*/
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);quick_sort(q, 0, n - 1);for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);return 0;
}
// 运行时间： 162 ms
// 运行空间： 1492 KB  

AcWing 786. 第k个数

原题链接

给定一个长度为 $n$ 的整数数列，以及一个整数 $k$，请用快速选择算法求出数列从小到大排序后的第 $k$ 个数。

输入格式

第一行包含两个整数 $n$ 和 $k$。

第二行包含 $n$ 个整数（所有整数均在 $1\sim 10^9$ 范围内），表示整数数列。

输出格式

输出一个整数，表示数列的第 $k$ 小数。

数据范围

$1\le n\le 100000$,
$1\le k\le n$

输入样例：

5 3
2 4 1 5 3

输出样例：

3

时/空限制： 1s / 64MB
来源： 模板题
算法标签：快速排序 快速选择

yxc’s Solution

• 如果直接用快速排序来做，那么时间复杂度就是 $O(n\log n)$ 了.

• 而快速选择算法的时间复杂度是 $O(n)$ 的.

• 类似于快速排序算法，对于数组 $\mathrm{q}[\mathrm{L}\sim \mathrm{R}]$，快速选择算法的流程如下：

  1. 确定分界点 $x$，一般取分界点 $x$ 为 $\mathrm{q}[\mathrm{L}]$ 或 $q[R]$ 或 $q[\lfloor \frac{L+R}{2}\rfloor ]$.
  2. 根据 $x$ 的值，将整个区间分为两半（调整区间），将 $⩽x$ 的数放到区间的左半部分，将 $⩾x$ 的数放到区间的右半部分.
  3. 假设左半部分数字的个数为 $S_L$，右半部分数字的个数为 $S_R$，若：
     • $k⩽S_L$，说明当前数组的第 $k$ 小的数在左半部分，此时只需要递归处理左半部分即可.
     • $k>S_L$，说明当前数组的第 $k$ 小的数在右半部分，此时只需要递归处理右半部分即可，不过需要注意的是，此时需要寻找的，是右半区间第 $k-S_L$ 小的数.

• 每次期望寻找的区间长度都会减少一半，则总的期望遍历次数为 $n+\frac{n}{2}+\frac{n}{4}+\cdots ⩽2n$，故总的期望时间复杂度为 $O(n)$.

  $1+\frac{1}{2}+\frac{1}{4}+\cdots =\underset{n\to +\infty }{\lim }\frac{1-\frac{1}{2^n}}{\frac{1}{2}}=2$.

#include <cstdio>
#include <algorithm>using namespace std;const int N = 1e5 + 10;int n, k;
int q[N];int quick_select(int q[], int L, int R, int k)
{if(L == R) return q[L];/*这里写 L == R 是因为我们时刻保证第 k 小的数在区间 [L,R] 的范围之内，所以区间 [L,R] 至少包含一个数，不会出现像快速排序那样需要写 L >=R （即区间可能没有数）的情况.*/int x = q[(L + R) / 2], i = L - 1, j = R + 1;while (i < j){while (q[ ++ i] < x);while (q[ -- j] > x);if (i < j) swap(q[i], q[j]);}int SL = j - L + 1;if (k <= SL) return quick_select(q, L, j, k);else return quick_select(q, j + 1, R, k - SL);
}int main()
{scanf("%d %d", &n, &k);for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);printf("%d", quick_select(q, 0, n - 1, k));return 0;
}
// 运行时间： 34 ms
// 运行空间： 596 KB 

AcWing 787. 归并排序

原题链接

给定你一个长度为 $n$ 的整数数列。

请你使用归并排序对这个数列按照从小到大进行排序。

并将排好序的数列按顺序输出。

输入格式

输入共两行，第一行包含整数 $n$。

第二行包含 $n$ 个整数（所有整数均在 $1\sim 10^9$ 范围内），表示整个数列。

输出格式

输出共一行，包含 $n$ 个整数，表示排好序的数列。

数据范围

$1\le n\le 100000$

输入样例：

5
3 1 2 4 5

输出样例：

1 2 3 4 5

时/空限制： 1s / 64MB
来源： 模板题
算法标签：归并排序

yxc’s Solution

• 归并排序的主要思想是分治.

• 对于一段待排序的数组 $\mathrm{q}[\mathrm{L}\sim \mathrm{R}]$ 来说，归并排序的算法流程如下：

  1. 确定分界点 $\mathrm{m}\mathrm{i}\mathrm{d}=\lfloor \frac{\mathrm{L}+\mathrm{R}}{2}\rfloor$.

  2. 递归，将数组的左半部分 $\mathrm{q}[\mathrm{L}\sim \mathrm{m}\mathrm{i}\mathrm{d}]$ 和右半部分 $\mathrm{q}[\mathrm{m}\mathrm{i}\mathrm{d}+1\sim \mathrm{R}]$ 分别先排好序.

  3. 归并，将左右两部分有序的数组合并为一个有序的数组.

• 如何将两个有序的数组合二为一是归并排序的重难点，实现方法如下：

  1. 用指针 $i$ 指向左半部分数组的开头 $\mathrm{q}[\mathrm{L}]$，用指针 $j$ 指向右半部分数组的开头 $\mathrm{q}[\mathrm{m}\mathrm{i}\mathrm{d}+1]$.

  2. 开辟一个新的数组 $\mathrm{r}\mathrm{e}\mathrm{s}$ 来合并后的数组.

  3. 比较 $\mathrm{q}[i]$ 和 $\mathrm{q}[j]$ 哪个更小，更小者放入数组 $\mathrm{r}\mathrm{e}\mathrm{s}$ 中，并让对应指针向后移动.

     • 当 $\mathrm{q}[i]=\mathrm{q}[j]$ 时，哪个放入数组 $\mathrm{r}\mathrm{e}\mathrm{s}$ 都一样，这里为了稳定，优先考虑将 $\mathrm{q}[i]$ 放入数组 $\mathrm{r}\mathrm{e}\mathrm{s}$ 中.

     • 因为这样可以保证 $\mathrm{q}[i]$ 和 $\mathrm{q}[j]$ 分别为两个数组中剩余所有数的最小值，则其中较小者就是剩余所有数中的最小值.

  4. 直到某一部分的指针指到了该部分对应的结尾，则剩下的另一部分的数组的剩余数字全部放入数组 $\mathrm{r}\mathrm{e}\mathrm{s}$，即可完成合并.

• 归并排序是稳定的排序算法，时间复杂度为 $O(n\log n)$.

  对于归并排序来说，每次都会从中间分开进行递归，整个递归的过程可以看作一棵二叉树.

  对于有 $n$ 个数的数组的归并排序，二叉树的叶子结点总共有 $n$ 个，则二叉树总共有 $\log n$ 层.

  每层都需要把数组合并在一起，每层的时间复杂度都为 $O(n)$.

  综合到一起，总的时间复杂度即 $O(n\log n)$.

#include <cstdio>
#include <iostream>using namespace std;const int N = 1e5 + 10;int n;
int q[N], res[N];void merge_sort(int q[], int L, int R)
{if (L >= R) return;int mid = (L + R) / 2;merge_sort(q, L ,mid); merge_sort(q, mid + 1, R);int k = L, i = L, j = mid + 1;while (i <= mid && j <= R)if (q[i] <= q[j]) res[k ++ ] = q[i ++ ];else res[k ++ ] = q[j ++ ];while (i <= mid) res[k ++ ] = q[i ++ ];while (j <= R) res[k ++ ] = q[j ++ ];for(i = L; i <= R; i ++ ) q[i] = res[i];
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);merge_sort(q, 0, n - 1);for (int i = 0; i < n; i ++ ) printf("%d ", q[i]);return 0;
}
// 运行时间： 95 ms
// 运行空间： 5460 KB 

AcWing 788. 逆序对的数量

原题链接

给定一个长度为 $n$ 的整数数列，请你计算数列中的逆序对的数量。

逆序对的定义如下：对于数列的第 $i$ 个和第 $j$ 个元素，如果满足 $i<j$ 且 $a[i]>a[j]$，则其为一个逆序对；否则不是。

输入格式

第一行包含整数 $n$，表示数列的长度。

第二行包含 $n$ 个整数，表示整个数列。

输出格式

输出一个整数，表示逆序对的个数。

数据范围

$1\le n\le 100000$，
数列中的元素的取值范围 $[1,10^9]$。

输入样例：

6
2 3 4 5 6 1

输出样例：

5

时/空限制： 1s / 64MB
来源： 模板题
算法标签：归并排序

yxc’s Solution

• 这里介绍利用归并排序求解逆序对.

• 对于一段待排序的数组 $\mathrm{q}[\mathrm{L}\sim \mathrm{R}]$ 来说，归并排序的算法流程如下：

  1. 确定分界点 $\mathrm{m}\mathrm{i}\mathrm{d}=\lfloor \frac{\mathrm{L}+\mathrm{R}}{2}\rfloor$.

  2. 递归，将数组的左半部分 $\mathrm{q}[\mathrm{L}\sim \mathrm{m}\mathrm{i}\mathrm{d}]$ 和右半部分 $\mathrm{q}[\mathrm{m}\mathrm{i}\mathrm{d}+1\sim \mathrm{R}]$ 分别先排好序.

  3. 归并，将左右两部分有序的数组合并为一个有序的数组，对于一个逆序对 $(x,y)$，此时有三种情况：

     1. $x,y$ 都在数组的左半部分；

     2. $x,y$ 都在数组的右半部分；

     3. $x$ 在数组的左半部分，$y$ 在数组的右半部分.

• 假设归并排序的递归过程，可以帮我们计算数组左半部分 $\mathrm{q}[\mathrm{L}\sim \mathrm{m}\mathrm{i}\mathrm{d}]$ 和右半部分 $\mathrm{q}[\mathrm{m}\mathrm{i}\mathrm{d}+1\sim \mathrm{R}]$ 的逆序对数量，那么此时就只需要计算第 3 种逆序对的数量就可以了，考虑如何计算：

  • 对于数组右半部分 $\mathrm{q}[\mathrm{m}\mathrm{i}\mathrm{d}+1\sim \mathrm{R}]$ 内的数 $\mathrm{q}[j]$，如果可以在数组左半部分 $\mathrm{q}[\mathrm{L}\sim \mathrm{m}\mathrm{i}\mathrm{d}]$ 中找到最小的数 $\mathrm{q}[i]$ 使得 $\mathrm{q}[i]>\mathrm{q}[j]$.
  • 则说明 $\mathrm{q}[i\sim \mathrm{m}\mathrm{i}\mathrm{d}]$ 区间内的数（共有 $\mathrm{m}\mathrm{i}\mathrm{d}-i+1$ 个）都 $>\mathrm{q}[j]$，因为 $\mathrm{q}[\mathrm{L}\sim \mathrm{m}\mathrm{i}\mathrm{d}]$ 已经先排好序了.

• 故只需在合并时，检查是否有 $\mathrm{q}[i]>\mathrm{q}[j]$，并计算答案即可（注意逆序对的数量可能超出 int 的表示范围）.

• 时间复杂度为 $O(n\log n)$.

#include <cstdio>
#include <iostream>using namespace std;typedef long long LL;
const int N = 1e5 + 10;int n;
LL ans;
int q[N], res[N];void merge_sort(int q[], int L, int R)
{if (L >= R) return;int mid = (L + R) / 2;merge_sort(q, L ,mid); merge_sort(q, mid + 1, R);int k = L, i = L, j = mid + 1;while (i <= mid && j <= R)if (q[i] <= q[j]) res[k ++ ] = q[i ++ ];else {ans += mid - i + 1;res[k ++ ] = q[j ++ ];}while (i <= mid) res[k ++ ] = q[i ++ ];while (j <= R) res[k ++ ] = q[j ++ ];for(i = L; i <= R; i ++ ) q[i] = res[i];
}int main()
{scanf("%d", &n);for (int i = 0; i < n; i ++ ) scanf("%d", &q[i]);merge_sort(q, 0, n - 1);printf("%lld", ans);return 0;
}
// 运行时间： 79 ms
// 运行空间： 4696 KB 

---

二分

---

• 二分重点讲一下整数二分，因为整数二分在实现时很容易写错、发生死循环、在边界的地方发生问题；然后再讲一下浮点数二分（即小数二分），它会比较简单一些.

• $二分\{\begin{array}{l}整数二分\\ 浮点数二分\end{array}$.

• 二分查找算法模板

• 整数二分的本质：

  • 二分的本质其实并不是单调性，也就是说，如果有单调性就可以二分，但可以二分题目不一定具有单调性；
  • 对于某一区间 $[\mathrm{L},\mathrm{R}]$，若我们在区间上定义了某种性质，使得性质在区间 $[\mathrm{x},\mathrm{R}]$ 内是满足的，而在区间 $[\mathrm{L},\mathrm{x}-1]$ 内是不满足的；
  • 那么整个区间就会根据这个性质一分为二，而二分就可以查找这个性质的边界，即 $\mathrm{x}$ 或 $\mathrm{x}-1$.

• 如果想要二分找到 $\mathrm{x}$，则实现方法：

  1. 取得中间值 $\mathrm{m}\mathrm{i}\mathrm{d}=\lfloor \frac{\mathrm{L}+\mathrm{R}}{2}\rfloor$.
  2. 如果 $\mathrm{m}\mathrm{i}\mathrm{d}$：
     • 满足性质，则说明至少 $[\mathrm{m}\mathrm{i}\mathrm{d},\mathrm{R}]$ 是满足性质的，且边界 $\mathrm{x}$ 就有可能是 $\mathrm{m}\mathrm{i}\mathrm{d}$，此时查找的区间就可以缩小到 $[\mathrm{L},\mathrm{m}\mathrm{i}\mathrm{d}-1]$.
     • 不满足性质，则说明至少 $[\mathrm{L},\mathrm{m}\mathrm{i}\mathrm{d}]$ 是不满足性质的，且边界 $\mathrm{x}$ 就不可能是 $\mathrm{m}\mathrm{i}\mathrm{d}$，此时查找的区间就可以缩小到 $[\mathrm{m}\mathrm{i}\mathrm{d}+1,\mathrm{R}]$.
  3. 直到 $\mathrm{L}>\mathrm{R}$，则最后一次可能作为边界 $\mathrm{x}$ 的 $\mathrm{m}\mathrm{i}\mathrm{d}$ 就一定是 $\mathrm{x}$.

  while (L <= R)
  {int mid = (L + R) / 2;if (check(mid)){ans = mid;R = mid - 1;}else L = mid + 1;
  }
  

• 无解的情况是与具体题目有关的，与二分的模板是无关的，可以发现二分的模板默认是有解的（当无解时，是不存在最后一次可能作为答案的 $\mathrm{m}\mathrm{i}\mathrm{d}$ 的）.

• 二分查找的时间复杂度为 $O(\log n)$，其中 $n$ 为二分查找的区间长度.

AcWing 789. 数的范围

原题链接

给定一个按照升序排列的长度为 $n$ 的整数数组，以及 $q$ 个查询。

对于每个查询，返回一个元素 $k$ 的起始位置和终止位置（位置从 $0$ 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式

第一行包含整数 $n$ 和 $q$，表示数组长度和询问个数。

第二行包含 $n$ 个整数（均在 $1\sim 10000$ 范围内），表示完整数组。

接下来 $q$ 行，每行包含一个整数 $k$ ，表示一个询问元素。

输出格式

共 $q$ 行，每行包含两个整数，表示所求元素的起始位置和终止位置。

如果数组中不存在该元素，则返回 -1 -1。

数据范围

$1\le n\le 100000$
$1\le q\le 10000$
$1\le k\le 10000$

输入样例：

6 3
1 2 2 3 3 4
3
4
5

输出样例：

3 4
5 5
-1 -1

时/空限制： 1s / 64MB
来源： 模板题,AcWing
算法标签：二分

yxc’s Solution

• 直接应用整数二分即可.
• 时间复杂度为 $O(q\log n)$.

#include <cstdio>
#include <iostream>using namespace std;const int N = 1e5 + 10;int n, q, k;
int a[N];int main()
{scanf("%d %d", &n, &q);for (int i = 0; i < n; i ++ ) scanf("%d", &a[i]);while (q -- ){scanf("%d", &k);int L = 0, R = n - 1, ansL = 0;while (L <= R){int mid = (L + R) / 2;if (a[mid] >= k){ansL = mid;R = mid - 1;} else L = mid + 1;}if (a[ansL] != k) {printf("-1 -1\n");continue;}L = 0, R= n - 1; int ansR = n; /*这里是寻找数组内第一个 > k 的数字的位置 ansR，此时有数组内最后一个 <=k 的数字的位置为 ansR-1，但数组内的数字可能都 <= k，故无解时 ansR 应为 n，此时对应数组内最后一个 <=k 的数字的位置为 n-1，即最后一个数字.*/while (L <= R){int mid = (L + R) / 2;if (a[mid] > k){ansR = mid;R = mid - 1;}else L = mid + 1;}printf("%d %d\n", ansL, ansR-1);}return 0;
}
// 运行时间： 71 ms
// 运行空间： 728 KB 

AcWing 790. 数的三次方根

原题链接

给定一个浮点数 $n$，求它的三次方根。

输入格式

共一行，包含一个浮点数 $n$。

输出格式

共一行，包含一个浮点数，表示问题的解。

注意，结果保留 $6$ 位小数。

数据范围

$-10000\le n\le 10000$

输入样例：

1000.00

输出样例：

10.000000

时/空限制： 1s / 64MB
来源： 模板题,AcWing
算法标签：二分

yxc’s Solution

• 浮点数二分和整数二分类似，它要求所寻找的答案一定在当前查找的区间之内.
• 当我们查找的区间长度很小时，我们就可以认为找到了答案.
• 时间复杂度为 $O(\log N)$，其中 $N$ 为二分查找的区间长度.

#include <cstdio>
#include <iostream>using namespace std;const double eps = 1e-7; 
/*这里的 eps 即为精度，因为题目要求保留 6 位小数，故我们要精确求解出 7 位小数才可以.
*/double n;int main()
{scanf("%lf", &n);double L = -1e5, R = 1e5;while(abs(R-L)>eps){double mid = (L + R) / 2;if (mid * mid * mid >= n) R = mid;else L = mid;}printf("%.6lf", L);return 0;
}
// 运行时间： 12 ms
// 运行空间： 220 KB 

---

本文档基于 AcWing算法基础课 制作

视频链接：第一章 基础算法（一）- AcWing

文档版本：

var1.0 完成于2022.04.26.