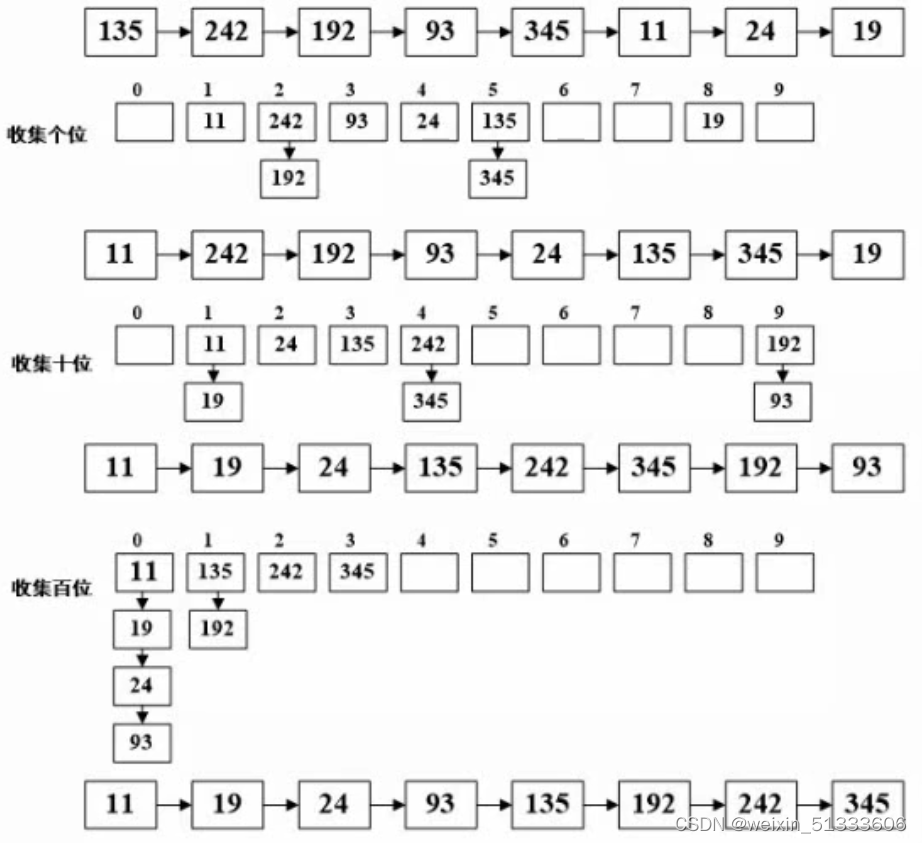
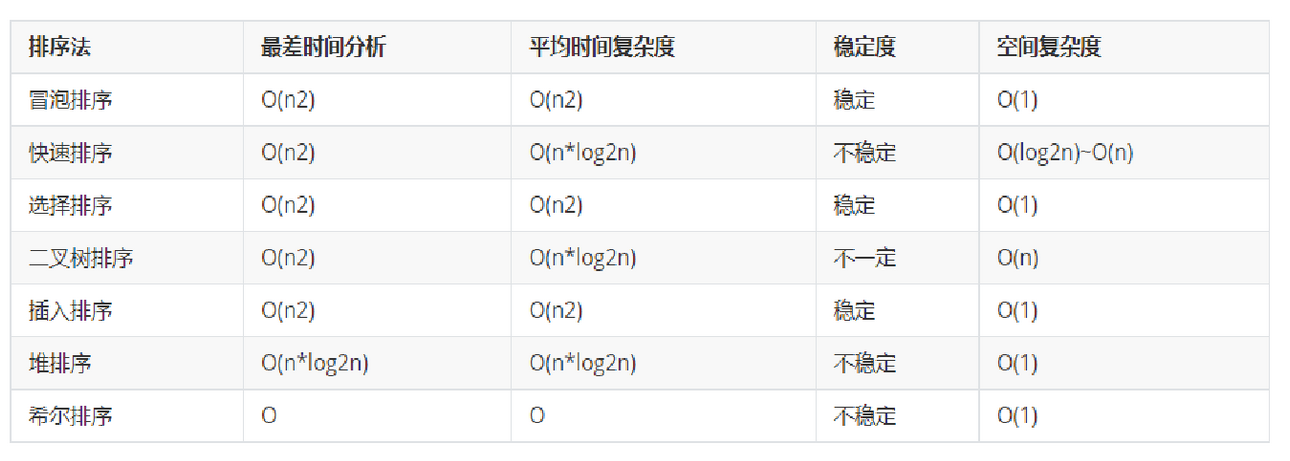
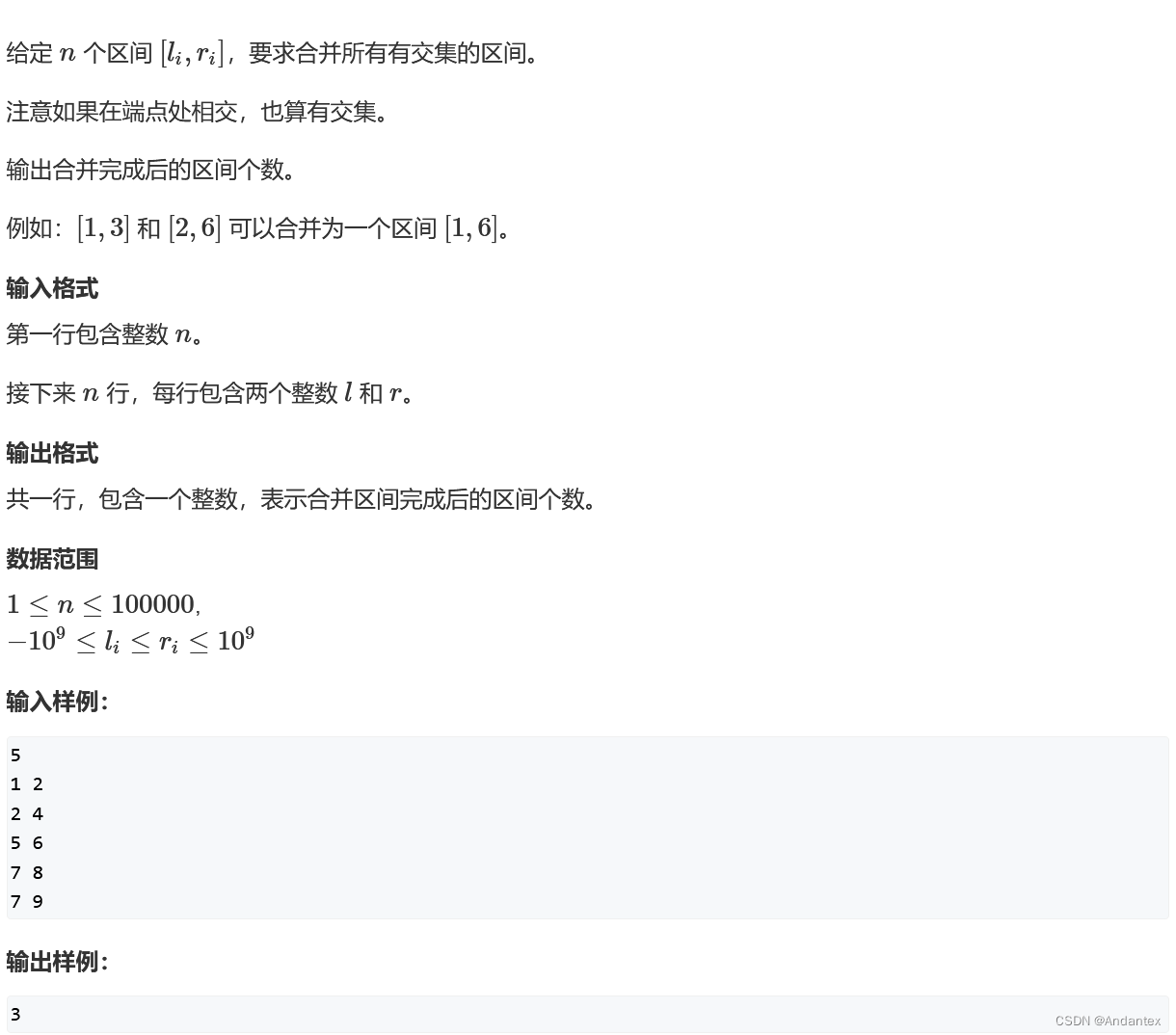
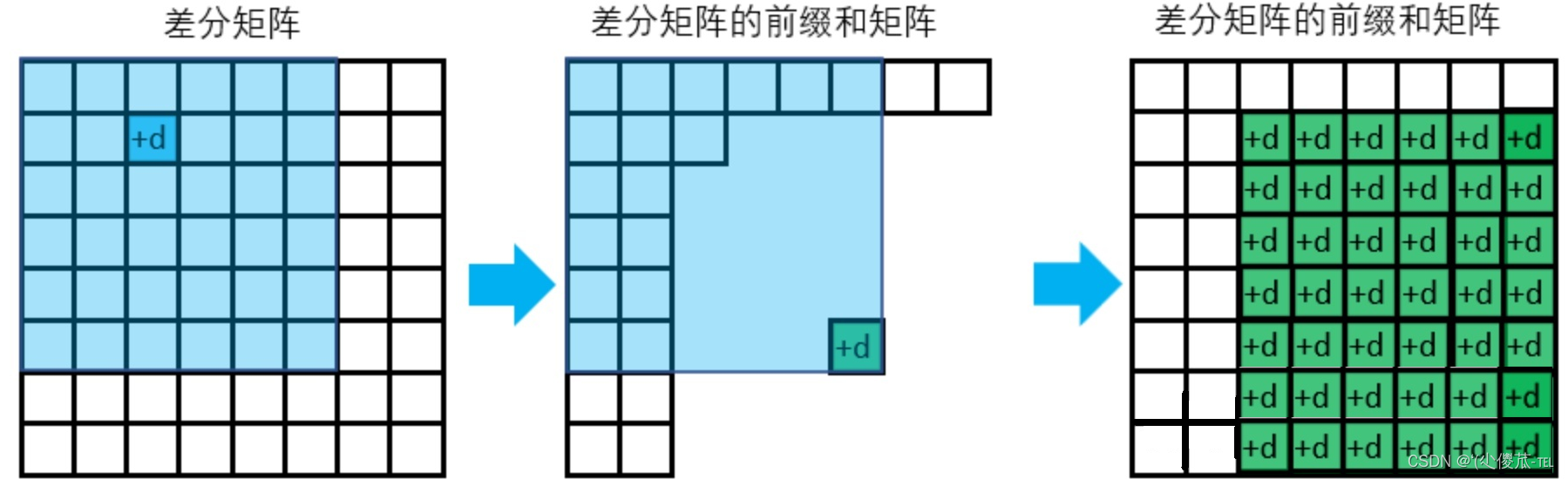
数学知识
- 第四章 数学知识
- 数论
- 质数
- 约数
- 欧拉函数
- 欧拉定理与费马小定理
- 拓展欧几里得定理
- 裴蜀定理
- 中国剩余定理
- 快速幂
- 高斯消元
- 求组合数
- 卡特兰数
- 容斥原理
- 博弈论
- Nim游戏
- SG函数
第四章 数学知识
数论
质数
- 质数判定:试除法,枚举时只枚举 i ≤ n i i \leq \frac{n}{i} i≤in即可(这里是防止整数溢出所以没有算平方)
- 分解质因数:试除法
- 首先 n n n中至多只包含一个大于 n \sqrt n n的质因子
- 所以仍然可以枚举 i ≤ n i i \leq \frac{n}{i} i≤in,每一次枚举,如果 i i i能整除 n n n,就把 n n n中的 i i i除尽
- 最后如果 n > 1 n>1 n>1,说明剩下了一个大于 n \sqrt n n的质因子,单独处理之即可
- 素数筛
-
朴素做法:从2到 n n n枚举,遇到没被筛掉的,把该数加到素数集合里,并把其所有倍数筛掉。时间复杂度 O ( n l o g n ) O(nlogn) O(nlogn)
-
由于质因数分解,所以在筛的时候,只需要筛掉所有质数的因数
int primes[N],cnt; bool st[N];void get_prime(int n){for(int i = 2;i<=n;i++){if(!st[i]){primes[cnt++] = n;for(int j = i+i;j <= n;j += ) st[j] = true;}} } -
线性筛:保证n只能被最小质因子筛掉
int primes[N],cnt; bool st[N];void get_prime(int n){for(int i = 2;i<=n;i++){if(!st[i]) primes[cnt++] = i;for(int j = 0;primes[j] <= n/i;j++){st[primes[j] * i] = true;if(i % primes[j] == 0) break; }} }- 合理性说明
- 若 i % p r i m e s [ j ] = 0 i\;\%\;primes[j] = 0 i%primes[j]=0: 因为是从小到大枚举目前已知的因子,所以 p r i m e s [ j ] primes[j] primes[j]一定是 i i i的最小质因子,那也一定是 p r i m e s [ j ] ∗ i primes[j]*i primes[j]∗i的最小质因子(相当于说 i i i在自己的基础上,不断去乘自己最小的质因子,那肯定最小质因子不会变)
- 若 i % p r i m e s [ j ] ≠ 0 i\;\%\;primes[j] \neq 0 i%primes[j]=0: 因为是从小到大枚举目前已知的因子,所以 p r i m e s [ j ] primes[j] primes[j]一定小于 i i i的最小质因子,那也一定是 p r i m e s [ j ] ∗ i primes[j]*i primes[j]∗i的最小质因子(相当于说 i i i在自己的基础上,不断去乘比自己最小的质因子 还小 的质因子,那最小质因子肯定是新乘进去的质因子)
- 以上两条保证了,所有数被筛去时,一定是被自己的最小质因子筛去的
- 对于一个任意的合数 x x x,设其最小质因子为 p j pj pj,在枚举到 x x x之前,一定会先枚举到 p j pj pj,这样 x x x一定会在枚举到他之前被筛去。而由于一个数的最小质因子只有一个,所以所有数只会被筛一次,所以该算法的复杂度是线性的
- 合理性说明
-
约数
-
试除法求一个数的约数:枚举时只枚举 d ≤ n d d \leq \frac{n}{d} d≤dn即可,因为约数肯定是成对出现的
-
约数个数:典中典之,质因数分解中,质因数的指数+1相乘。这样在试除法求分解质因数的算法里改改就行,每次不再记录质因数是谁,记录除了几次才除尽
-
约数之和,若 x = p 1 α 1 p 2 α 2 p 3 α 3 p 4 α 4 . . . p k α k x = p_{1}^{\alpha_1}p_{2}^{\alpha_2}p_{3}^{\alpha_3}p_{4}^{\alpha_4}...p_{k}^{\alpha_k} x=p1α1p2α2p3α3p4α4...pkαk 则有 s u m = ( p 1 0 + p 1 1 + . . . + p 1 α 1 ) ( p 2 0 + p 2 1 + . . . + p 2 α 2 ) . . . ( p k 0 + p k 1 + . . . + p k α k ) sum=(p_{1}^{0}+p_{1}^{1}+...+p_{1}^{\alpha_1})(p_{2}^{0}+p_{2}^{1}+...+p_{2}^{\alpha_2})...(p_{k}^{0}+p_{k}^{1}+...+p_{k}^{\alpha_k}) sum=(p10+p11+...+p1α1)(p20+p21+...+p2α2)...(pk0+pk1+...+pkαk)正确性验证只需要乘法分配律即可
- 细节:把 1 + p 2 + p 3 + . . . + p m 1+p^2+p^3+...+p^m 1+p2+p3+...+pm改成递归的计算法 [ ( [ ( p + 1 ) ∗ p ] + 1 ) ∗ p ] . . . [([(p+1)*p]+1)*p]... [([(p+1)∗p]+1)∗p]...即每次都是乘p再加1
#include <bits/stdc++.h> using namespace std; typedef long long int ll;const int N = 1e9+7;int main(){int x;cin>>x;unordered_map<int,int> primes;for(int i = 0;i <= x/i;i++){while(x%i == 0){x /= i;primes[i]++;}}if(x > 1) primes[x] ++;ll res = 1;for(auto prime : primes){int p = prime.first, a = prime.second;ll t = 1;while(a--){t = (t*p + 1) % N;}res = res * t % N;}cout << res << endl;return 0; } -
最大公约数,辗转相除法。 a > b , g c d ( a , b ) = b ? g c d ( b , a % b ) : a a>b\;,\;gcd(a,b)=b\;?\;gcd(b,a\%b)\;:\;a a>b,gcd(a,b)=b?gcd(b,a%b):a
- 这是基于基本的观察 a % b = a − ⌊ a b ⌋ ∗ b a\%b = a - \lfloor\frac{a}{b}\rfloor * b a%b=a−⌊ba⌋∗b
- 所以我们总是有 g c d ( a , b ) = g c d ( b , a % b ) gcd(a,b) = gcd(b,a\%b) gcd(a,b)=gcd(b,a%b)
欧拉函数
ϕ ( n ) = 1 到 n 里所有与 n 互质的数的个数 \phi (n) = 1到n里所有与n互质的数的个数 ϕ(n)=1到n里所有与n互质的数的个数
i f N = p 1 α 1 p 2 α 2 . . . p k α k if \; N = p_1^{\alpha _1}p_2^{\alpha _2}...p_k^{\alpha _k} ifN=p1α1p2α2...pkαk
t h e n ϕ ( N ) = N ( 1 − 1 p 1 ) ( 1 − 1 p 2 ) . . . ( 1 − 1 p k ) then \ \phi(N) = N(1-\frac{1}{p_1})(1-\frac{1}{p_2})...(1-\frac{1}{p_k}) then ϕ(N)=N(1−p11)(1−p21)...(1−pk1)
原理:容斥原理:展开来即可 N − ( N p 1 + N p 2 + . . . + N p k ) + ( N p i ∗ p j ) + . . . − . . . N - (\frac{N}{p_1}+\frac{N}{p_2}+...+\frac{N}{p_k})+(\frac{N}{p_i*p_j})+...-... N−(p1N+p2N+...+pkN)+(pi∗pjN)+...−...
朴素做法就是一边进行质因数分解一边求每一项 n / ( p i ) ∗ ( p i − 1 ) n/(p_i)*(p_i-1) n/(pi)∗(pi−1)
下面给出线性筛改进的做法

其本质思想是通过已有的欧拉函数值不断推导没有的,而正好能一边筛,一边进行推导
要把握住本质,就是欧拉函数的计算公式和线性筛的原理
int primes[N],cnt;
int phi[N];
bool st[N];ll get_phis(int n){for(int i = 2;i <= n;i++){if(!st[i]){primes[cnt++] = i;phi[i] = i-1;//如果i是质数,欧拉函数就是i-1}for(int j = 0;primes[j] <= n/i;j++){//接下来的推导都要结合欧拉函数的公式看st[primes[j]*i] = true;if(i % primes[j] == 0){phi[primes[j] * i] = phi[i]*primes[j];//如果i能够整除pj,所以pj是i的最小质因子,所以pj*i与pj的质因数是各质因子相同,次数不同。break;}phi[primes[j]*i] = phi[i]*(primes[i]-1);//如果不能整除,说明pj*i只是添加了一个最小的质因子}}
}
欧拉定理与费马小定理
欧拉定理
若 a 与 n 互质,则 a ϕ ( n ) ≡ 1 ( m o d n ) 若a与n互质,则 a^{\phi (n)} \equiv 1(mod \ n) 若a与n互质,则aϕ(n)≡1(mod n)
证明的话acwing讲的太亏贼了,建议看看这个(https://blog.csdn.net/weixin_43145361/article/details/107083879)
费马小定理就是一个欧拉定理的特例
在欧拉定理里取 n 为质数 p ,有 a p − 1 ≡ 1 ( m o d p ) 在欧拉定理里取n为质数p,有a^{p-1} \equiv 1(mod \ p) 在欧拉定理里取n为质数p,有ap−1≡1(mod p)
一个应用就是求在模n的意义下的乘法逆元,即 b − 1 : = b ∗ b − 1 ≡ 1 ( m o d m ) b^{-1} := b*b^{-1} \equiv 1(mod \ m) b−1:=b∗b−1≡1(mod m)
这种的逆元,由欧拉定理, 若 b 与 m 互质,则 b ϕ ( n ) − 1 = b − 1 若b与m互质,则 b^{\phi (n)-1}=b^{-1} 若b与m互质,则bϕ(n)−1=b−1
拓展欧几里得定理
裴蜀定理
- 对于任意的正整数 ( a , b ) (a,b) (a,b) 一定存在 ( x , y ) (x,y) (x,y),使得 a x + b y = g c d ( a , b ) ax+by = gcd(a,b) ax+by=gcd(a,b)
- 对于任意的可被表示成 a x + b y ax+by ax+by形式的整数 d d d,都一定有 d m o d g c d ( a , b ) = 0 d \ mod \ gcd(a,b) =0 d mod gcd(a,b)=0
拓展欧几里得算法就是对其的一个构造
int exgcd(int a,int b,int &x,int &y){//自底向上更新if(!b){x = 1,y = 0;return a;}int gcd = exgcd(b,a%b,y,x);//注意这里反向传参,更新时能少写点y -= a/b*x;return gcd;
}
这是基于下面的演算
- 若b=0,则 a ∗ 1 + b ∗ 0 = g c d ( a , b ) = a a*1 + b*0 = gcd(a,b) = a a∗1+b∗0=gcd(a,b)=a,所以取 x = 1 , y = 0 x=1,y=0 x=1,y=0,作为递归退出条件
- 若已经有下一层的递归结果,如何更新本层:
- 注意到若已有 b x ∗ + ( a % b ) y ∗ = g c d ( b , a % b ) bx^{*}+(a\%b)y^{*}=gcd(b,a\%b) bx∗+(a%b)y∗=gcd(b,a%b)
- 带入余数公式,整理得 a y ∗ + b ( x ∗ − ⌊ a b ⌋ y ∗ ) = g c d ( b , a % b ) = g c d ( a , b ) ay^{*}+b(x^{*}- \lfloor \frac{a}{b} \rfloor y^{*}) = gcd(b,a\%b) = gcd(a,b) ay∗+b(x∗−⌊ba⌋y∗)=gcd(b,a%b)=gcd(a,b)
- 所以做以下更新 x = y ∗ , y = x ∗ − ⌊ a b ⌋ y ∗ x = y^{*},y = x^{*}- \lfloor \frac{a}{b} \rfloor y^{*} x=y∗,y=x∗−⌊ba⌋y∗
拓展欧几里得算法也可用于求逆元,这是因为对于方程 a x ≡ 1 ( m o d m ) ax \equiv 1(mod \ m) ax≡1(mod m)
总可以化为 a x + m y = 1 ax+my = 1 ax+my=1,其中y是任意整数
于是可以用拓展欧几里得给出
中国剩余定理
问题 { m 1 , m 2 , . . . , m k } \{m_1,m_2,...,m_k\} {m1,m2,...,mk} 两两互质,给出关于x的一组方程,求解x
{ x ≡ a 1 ( m o d m 1 ) x ≡ a 2 ( m o d m 2 ) ⋮ x ≡ a k ( m o d m k ) \begin{cases} x \equiv a_1 (mod \ m_1)\\ x \equiv a_2 (mod \ m_2)\\ \vdots x \equiv a_k (mod \ m_k)\\ \end{cases} ⎩ ⎨ ⎧x≡a1(mod m1)x≡a2(mod m2)⋮x≡ak(mod mk)
解
令 M = m 1 m 2 . . . m k , M i = M m i M=m_1m_2...m_k,M_i = \frac{M}{m_i} M=m1m2...mk,Mi=miM
再令 M i − 1 M_i^{-1} Mi−1为其在取模 m i m_i mi意义下的乘法逆元
则有 x = a 1 M 1 M 1 − 1 + a 1 M 1 M 1 − 1 + . . . + a k M k M k − 1 x = a_1M_1M_1^{-1}+a_1M_1M_1^{-1}+...+a_kM_kM_k^{-1} x=a1M1M1−1+a1M1M1−1+...+akMkMk−1
其中乘法逆元用拓展欧几里得算法求得
快速幂
在 O ( l o g k ) O(logk) O(logk)时间复杂度内计算 a k m o d p a^k \ mod \ p ak mod p的结果
思路:反复平方法
若 k = ( x l o g k x l o g k − 1 . . . x 1 x 0 ) ( 2 ) k=(x_{logk}x_{logk-1}...x_{1}x_{0})_{(2)} k=(xlogkxlogk−1...x1x0)(2)
则 a k = a 2 i 1 + 2 i 2 + 2 i 3 . . . + 2 i l a^k = a^{2^{i_1}+2^{i_2}+2^{i_3}...+2^{i_l}} ak=a2i1+2i2+2i3...+2il其中 i j i_j ij满足 0 ≤ i j ≤ l o g k ∧ x i j = 1 0 \leq i_j \leq logk\ \land \ x_{i_j}=1 0≤ij≤logk ∧ xij=1即那些二进制表示k中是1的那些位
typedef long long int ll;
int qpow(int a,int k,int p){int res = 1;while(k){if(k & 1) res = (ll)res*a%p;//如果k的二进制最后一位是1k >>= 1;//算下一位a = (ll)a*a%p;//把a平方}return res;
}
其中不断平方的作用是其实是不断计算 a 2 0 , a 2 1 , a 2 2 . . . , a 2 l o g k a^{2^0},a^{2^1},a^{2^2}...,a^{2^{logk}} a20,a21,a22...,a2logk然后用这些计算出来的幂次来组合出a的幂次
高斯消元
我超,来点线性代数(数值分析?)
这里讲的是列主元法
- 找到当前列中,行序号大于等于当前行的元素中,绝对值最大的元素(这里是为了精度,见数值分析)
- 把其所在行交换至当前的顶部
- 把该行全部除以第一个元素,将第一个元素变成1
- 用该行将下面所有行的当前列消成0
- 向右下移动,重复以上过程,直到矩阵变成阶梯型
- 最后进行解的情况判断,如果有解,则倒推解出各未知数
来点代码
#include <bits/stdc++.h>
using namespace std;int n;
const double eps = 1e-6;//浮点数判等精度
const int N = 110;
double a[N][N];int gauss(){int c,r;//列数,行数for(c = 0,r = 0;c<n;c++){//从左向右遍历所有列,同时行号r从0开始int t = r;//t存储具有最大绝对值的元素的行号for(int i = r;i<n;i++){//从上到下遍历行来寻找绝对值最大的if(fabs(a[i][c] > fabs(a[t][c]))) t = i;}if(fabs(a[t][c])<eps) continue;//如果是0,说明这一列全是0了,那就不管了for(int i = c;i <= n;i++ ) swap(a[t][i],a[r][i]);//交换两行for(int i = n;i >= c;i--) a[r][i] /= a[r][c];//将该行的第一个元素消成1,注意要倒着处理for(int i = r+1;i<n;i++){//从当前行向下,把大火的第一个元素都搞成0if(fabs(a[i][c])>eps){//判断一下第一个元素是不是已经是0了for(int j = n;j >= c;j--){a[i][j] -= a[r][j]*a[i][c];//把第i行处理一下}}}r++;//向右下移动}if(r<n){//说明系数矩阵的秩小于nfor(int i = r;i < n;i++){if(fabs(a[i][n])>eps){//如果全系数矩阵该行全是0,但是延拓矩阵不是0return -1;//无解}}return 0;//否则有无穷多组解}for(int i = n-1;i >= 0;i++){for(int j = i+1;j<n;j++){a[i][n] -= a[i][j] * a[j][n];//倒退解出各个未知数}}return 1;//有唯一解
}
求组合数

看a,b,n的范围,如果每次询问都硬用连乘计算,那就有 O ( n b ) O(nb) O(nb)的复杂度,在本题条件是不能接受的
注意到杨辉三角的递推式 C a b = C a − 1 b + C a − 1 b − 1 C_{a}^{b} = C_{a-1}^{b}+C_{a-1}^{b-1} Cab=Ca−1b+Ca−1b−1
所以可以在 O ( a 2 ) O(a^2) O(a2)的时间内预处理出所有的结果,这样每次进行查询时查表即可,整个时间复杂度成为 o ( a 2 + n ) o(a^2+n) o(a2+n),在本题范围下是更优的做法
#include <bits/stdc++.h>
using namespace std;const int N = 2010,MOD = 1e9+7;int c[N][N];void init(){for(int i = 0;i<N;i++){for(int j = 0;j <= i;j++){if(!j) c[i][j] = 1;else c[i][j] = (c[i-1][j]+c[i-1][j-1]) % MOD;}}
}int main(){init();int n;scanf("%d",&n);while(n--){int a,b;scanf("%d%d",&a,&b);printf("%d\n",c[a][b]);}return 0;
}

本题a的范围过大,预处理出所有组合数不现实,所以换一种预处理方法
注意到组合数可由阶乘组合出,所以策略是先预处理出所有数的阶乘和阶乘的乘法逆元(因为该题都是在模p的意义下讨论的)
阶乘可以递推,阶乘的乘法逆元用费马定理加快速幂求,总的时间复杂度是 O ( a l o g a + k ) O(aloga+k) O(aloga+k)
#include <bits/stdc++.h>
using namespace std;typedef long long int ll;
const int N = 10, MOD = 1e9 + 7;int fact[N], infact[N];int qpow(int a, int k, int p) {int res = 1;while (k) {if (k & 1) res = (ll)res * a % p;a = (ll)a * a % p;k >>= 1;}return res;
}void init() {fact[0] = infact[0] = 1;for (int i = 1; i < N; i++) {fact[i] = (ll)fact[i - 1] * i % MOD;infact[i] = (ll)infact[i - 1] * qpow(i, MOD - 2, MOD) % MOD;}
}int main() {init();int n;scanf("%d",&n);while (n--) {int a, b;scanf("%d%d", &a, &b);printf("%lld\n", (ll)fact[a]*infact[b]%MOD*infact[a - b] % MOD);}return 0;
}

本题是询问次数少,但是需要求的组合数范围大,以上的预处理方案都不符合条件了。
考虑卢卡斯定理
C a b ≡ C a % p b % p C a / p b / p ( m o d p ) C^{b}_{a} \equiv C^{b\%p}_{a\%p}\;C^{b/p}_{a/p} \ (mod \ p) Cab≡Ca%pb%pCa/pb/p (mod p)
证明:
- 首先有 ( 1 + x ) p k ≡ 1 + x p k ( m o d p ) (1+x)^{p^k} \equiv 1+x^{p^k}\;(mod \ p) (1+x)pk≡1+xpk(mod p)直接展开对p取余即得
- 写出a,b的p进制数字,即 a = ( a k a k − 1 … a 1 a 0 ) ( p ) , b = ( b l b l − 1 … b 1 b 0 ) ( p ) a=(a_ka_{k-1} \dots a_1a_0)_{(p)},b=(b_lb_{l-1} \dots b_1b_0)_{(p)} a=(akak−1…a1a0)(p),b=(blbl−1…b1b0)(p)
- 考虑生成函数 ( 1 + x ) a = ( 1 + x ) a 0 ( 1 + x ) p 1 a 1 ( 1 + x ) p 2 a 2 … ( 1 + x ) p k a k (1+x)^a = (1+x)_{a_0}(1+x)^{p^{1}a_{1}}(1+x)^{p^{2}a_{2}} \dots (1+x)^{p^{k}a_{k}} (1+x)a=(1+x)a0(1+x)p1a1(1+x)p2a2…(1+x)pkak
- 对p取余,有 ( 1 + x ) a ≡ ( 1 + x ) a 0 ( 1 + x p 1 ) a 1 … ( 1 + x p k ) a k (1+x)^a \equiv (1+x)^{a_0}(1+x^{p^1})^{a_{1}} \dots (1+x^{p^k})^{a_{k}} (1+x)a≡(1+x)a0(1+xp1)a1…(1+xpk)ak
- 观察两侧 x b x^b xb项的系数
#include <bits/stdc++.h>
using namespace std;typedef long long int ll;int p;int qpow(int a, int k, int p) {int res = 1;while (k) {if (k & 1) res = (ll)res * a % p;a = (ll)a * a % p;k >>= 1;}return res;
}int C(int a,int b){//直接爆算int res = 1;for(int i = 1,j = a;i <= b;i++,j--){res = (ll)res*j%p;res = (ll)res*qpow(i,p-2,p)%p;//快速幂逆元}return res;
}int lucas(ll a,ll b){if(a < p && b<p) return C(a,b);return (ll)C(a%p,b%p)*lucas(a/p,b/p) %p;//递归调用
}int main(){int n;cin >> n;while(n--){ll a,b;cin >> a >> b >> p;cout << lucas(a,b) << endl;}return 0;
}

需要用高精度,考虑到时间复杂度和代码的好写,只用高精度乘法
方法是对组合数进行质因数分解
C b a = a ! b ! ( a − b ) ! ,于是考察质因子 p 在分子中的次数和在分母中的次数 C_{b}^{a} = \frac{a!}{b!(a-b)!},于是考察质因子p在分子中的次数和在分母中的次数 Cba=b!(a−b)!a!,于是考察质因子p在分子中的次数和在分母中的次数
统计阶乘的质因数 c n t ( p i n n ! ) = ⌊ n p 1 ⌋ + ⌊ n p 2 ⌋ + ⌊ n p 3 ⌋ + … cnt(p \ in \ n!) = \lfloor \frac{n}{p^{1}} \rfloor +\lfloor \frac{n}{p^{2}} \rfloor +\lfloor \frac{n}{p^{3}} \rfloor + \dots cnt(p in n!)=⌊p1n⌋+⌊p2n⌋+⌊p3n⌋+…其实就是统计1到n中p这个因子出现了几次
本题思路:
- 先预处理出素数序列
- 然后对于所有素数,统计其在组合数的质因数分解中出现的次数
- 就是分别对分子分母上的阶乘统计其出现的次数
- 然后分子出现的次数减去分母上出现的次数
- 用高精度乘法把质因数乘起来
#include <bits/stdc++.h>
using namespace std;const int N = 10;//素数筛部分
int primes[N],idx;
bool st[N];
void getprimes(int n){for(int i = 2;i<=n;i++){if(!st[i]) primes[idx++] = i;for(int j = 0;primes[j] <= n/i;j++){st[primes[j]*i] = true;if(i % primes[j] == 0) break;}}
}//统计质因数
int ct[N];
int cnt(int n,int p){int res = 0;while(n){res += n/p;n /= p;}return res;
}//高精度乘法
vector<int> mul(vector<int> &a,int b){vector<int> c;int t = 0;for(int i = 0;i<a.size();i++){t += a[i]*b;c.push_back(t % 10);t /= 10;}while(t){c.push_back(t%10);t /= 10;}return c;
}int main(){int a,b;cin >> a >> b;getprimes(a);for(int i = 0;i<idx;i++){int p = primes[i];ct[i] = cnt(a,p)-cnt(b,p)-cnt(a-b,p);}vector<int> res;res.push_back(1);for(int i = 0;i < idx;i++){for(int j = 0;j<ct[i];j++){res = mul(res,primes[i]);}}for(int i =res.size() - 1;i >= 0;i--) printf("%d",res[i]);puts("");return 0;
}
小结
- 先从要算的组合数的参数开始判断,从小到大的策略分别是
- 直接预处理出所有组合数,方法是杨辉三角式的递推
- 直接预处理出所有阶乘和所有阶乘的逆
- 卢卡斯定理,递归,不断把规模变小
- 如果题目中要求求精确值,直接高精度
卡特兰数

几何含义:从原点 ( 0 , 0 ) (0,0) (0,0)走到 ( n . n ) (n.n) (n.n),且在任何时刻都不在直线 y = x y=x y=x分割的区域中的上半区域
的路径的数量
(意思就是0是向右走一步,1意思向上走一步,则构造了一个序列到路径的映射)
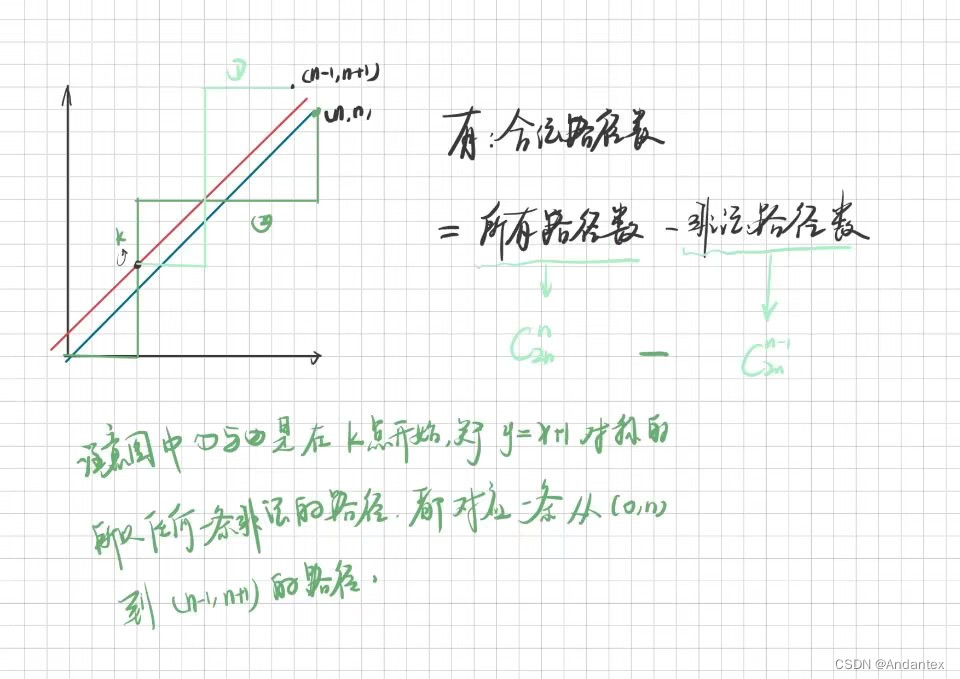
所以最终答案就是 C 2 n n − C 2 n n = C 2 n n n + 1 C_{2n}^{n} - C_{2n}^{n} = \frac{C_{2n}^{n}}{n+1} C2nn−C2nn=n+1C2nn
还是采用预处理出所有阶乘和阶乘的逆元的方式
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;const int N = 200010, mod = 1e9 + 7;int n;
int fact[N], infact[N];int qpow(int a, int k) {int res = 1;while (k) {if (k & 1) res = (ll)res * a % mod;a = (ll)a * a % mod;k >>= 1;}return res;
}void init() {fact[0] = infact[0] = 1;for (int i = 1; i < N; i++) {fact[i] = (ll)fact[i - 1] * i % mod;infact[i] = (ll)infact[i - 1] * qpow(i, mod - 2) % mod;}
}int main() {init();cin >> n;int res = (ll)fact[2 * n] * infact[n] % mod * infact[n] % mod * qpow(n + 1, mod - 2) % mod;cout << res << endl;return 0;
}
容斥原理

- 共有 2 n − 1 2^{n-1} 2n−1项,所以时间复杂度是 O ( 2 n ) O(2^n) O(2n)

容斥原理里重要的一步就是选择合适的方法遍历所有 2 n 2^n 2n个状态,一般的做法是进行DFS。这里选择的是用二进制数进行状态压缩。
具体来说就是用一个n位的二进制数来表示求“拿出哪些集合出来求∩”。
#include <bits/stdc++.h>
using namespace std;
typedef long long int ll;const int N = 20;
int p[N];
int n,m;int main(){cin >> n >> m;for(int i = 0;i<m;i++) cin>>p[i];int res = 0;for(int i = 1;i < 1 << m;i++){//枚举所有状态int t = 1,cnt = 0;//i记录素数的乘积,cnt表示乘了几个质数for(int j = 0;j<m;j++){if(i >> j & 1){//判断该位是不是0cnt ++;if((ll)t*p[j] > n){t = -1;break;}t *= p[j];}}if(t != -1){if(cnt%2) res += n/t;else res -= n/t;}}cout << res << endl;return 0;
}
博弈论
Nim游戏

结论 { a i } \{a_i\} {ai}是石子个数,则 a 1 ⊕ a 2 ⊕ a 3 ⊕ … a n = 0 a_1 \oplus a_2 \oplus a_3 \oplus \dots a_n = 0 a1⊕a2⊕a3⊕…an=0先手必败,反之必胜
证明
- 首先证明若 a 1 ⊕ a 2 ⊕ a 3 ⊕ … a n = x ≠ 0 a_1 \oplus a_2 \oplus a_3 \oplus \dots a_n = x \neq 0 a1⊕a2⊕a3⊕…an=x=0,则一定有一个策略给他拿成0
- 设x的二进制数的最高位1在k位
- 则在所有 a i a_i ai中,一定存在 a j a_j aj,其第k位是1
- 那取 a j ⊕ x a_j \oplus x aj⊕x,则一定把 a j a_j aj的第k位搞成了0,则一定有 a j ⊕ x < a j a_j \oplus x < a_j aj⊕x<aj
- 那我直接把 a j a_j aj这堆石子取成 a j ⊕ x < a j a_j \oplus x < a_j aj⊕x<aj ,对整体异或的效果就是x再异或x,由异或的性质,这样就给出了一个把异或值拿成0的策略
- 其次,若当前 a 1 ⊕ a 2 ⊕ a 3 ⊕ … a n = 0 a_1 \oplus a_2 \oplus a_3 \oplus \dots a_n = 0 a1⊕a2⊕a3⊕…an=0,则一定不存在使得拿完后异或值还是0的策略
- 反证,倘若拿完后, a j a_j aj变成 a j ′ a_{j}^{'} aj′,总体异或值还是0
- 把前后所有值都异或起来,得到 a j ⊕ a j ′ = 0 a_j \oplus a_{j}^{'} = 0 aj⊕aj′=0,这说明 a j = a j ′ a_j = a_{j}^{'} aj=aj′,矛盾
- 这样只要初始状态是不等于0的,那先手的人总可以保证,在自己走完这一步后,对面面临的是异或为0的状态,则拿完后回到手里又是异或不等于0的状况。这样不断循环,对方只能保持在石子数量不断减少的情况下,异或值还是0。这样对面的状态最后一定会到达所有石子堆都变成0
- 于是此时先手必胜
SG函数
有向图游戏
- Mex运算: S 为由非负整数的集合, M e x ( S ) : = m i n { x } , s . t . x ∈ N ∧ x ∉ S S为由非负整数的集合,Mex(S):=min\{x\},s.t. \ x \in \N \land x \notin S S为由非负整数的集合,Mex(S):=min{x},s.t. x∈N∧x∈/S
- 某节点x的SG函数:递归定义
- 若x为终点,则 S G ( x ) = 0 SG(x) = 0 SG(x)=0
- 若x不为终点,则设 { y 1 , y 2 , … , y k } \{y_1,y_2,\dots ,y_k\} {y1,y2,…,yk}是x的邻居,则 S G ( x ) = M e x ( { S G ( y 1 ) , S G ( y 1 ) , … , S G ( y k ) } ) SG(x) = Mex(\{SG(y_1),SG(y_1),\dots,SG(y_k)\}) SG(x)=Mex({SG(y1),SG(y1),…,SG(yk)})
- 某个有向图G的SG函数: S G ( G ) : = S G ( s t ) , s t 是 G 的起点 SG(G):=SG(st),st是G的起点 SG(G):=SG(st),st是G的起点
- 对于一个有向图游戏 { G i } \{G_i\} {Gi},定义其状态值为 S G ( { G i } ) : = S G ( G 1 ) ⊕ S G ( G 2 ) ⋯ ⊕ S G ( G n ) SG(\{G_i\}):=SG(G_1) \oplus SG(G_2) \dots \oplus SG(G_n) SG({Gi}):=SG(G1)⊕SG(G2)⋯⊕SG(Gn)
对于一个有向图游戏,有 S G ( { G i } ) ≠ 0 SG(\{G_i\}) \neq 0 SG({Gi})=0必胜,反之必败
证明方法可逐步照搬nim游戏的必胜策略证明
例题:

思路:
- 每堆石子都是一个有向图
#include <bits/stdc++.h>
using namespace std;const int N = 110, M = 10010;
int n, m;
int f[M], s[N];
//f是一个记忆化搜索数组,这是注意到只要石子的个数相同,则其派生出的有向图是相同的
//所以石子个数和其sg值是一一对应的,所以开一个数组来存储所有可能的sg值
//一边搜索一边存储,所以是记忆化搜int sg(int x) {//对于每一堆石子,用记忆化搜索,算出其作为有向图的头节点的sg值if (f[x] != -1) return f[x];unordered_set<int> S;//该集合存x出发前可以到达的所有状态for (int i = 0; i < m; i++) {int sum = s[i];//枚举所以可能的拿法if (x >= sum) S.insert(sg(x - sum));//dfs}for (int i = 0;; i++)//mex函数if (!S.count(i))return f[x] = i;
}int main() {cin >> m;for (int i = 0; i < m; i++) cin >> s[i];cin >> n;memset(f, -1, sizeof(f)); //-1代表还没被搜索过int res = 0;for (int i = 0; i < n; i++) {int x;cin >> x;res ^= sg(x);}if (res) printf("Yes");else printf("No");return 0;
}