synchronized 有三种方式来加锁，分别是：
**1. 修饰实例方法：**作用于当前实例加锁，进入同步代码前要获得当前实例的锁
**2. 静态方法：**作用于当前类加锁，进入同步代码前要获得当前类的锁
**3. 修饰代码块：**指定加锁对象：对给定对象加锁，进入同步代码库前要获得给定对象的锁

思考锁是如何存储的

我们以对象在 jvm 内存中是如何存储作为切入点，去看看对象里面有什么特性能够实现锁
锁的状态标识就是存放在对象的存储空间中，虚拟机中对对象的存储分为三部分：
对象头、实例数据、对齐填充

对象头分为两部分：一部分称为Mark Word，不同位数虚拟机上存储长度不一样，32位虚拟机上是32bits，64位虚拟机上是64bits；另一部分是类型信息的指针
Mark Word的存储结构并不是固定不变的，虚拟机会根据锁的状态调整存储，充分利用存储空间，如下图不同的锁状态对应的数据的不同存储方式

为什么任何对象都可以实现锁

1. 首先，Java 中的每个对象都派生自 Object 类，而每个Java Object 在 JVM 内部都有一个 native 的 C++对象oop/oopDesc 进行对应。
2. 线程在获取锁的时候，实际上就是获得一个监视器对象(monitor) ,monitor 可以认为是一个同步对象，所有的Java 对象天生携带 monitor。多个线程访问同步代码块时，相当于去争抢对象监视器修改对象中的锁标识

synchronized 锁的升级
在分析几种锁的区别之前，我们先来思考一个问题
使用锁能够实现数据的安全性，但是会带来性能的下降
不使用锁能够基于线程并行提升程序性能，但是却不能保证线程安全性。这两者之间似乎是没有办法达到既能满足性能也能满足安全性的要求

其实大部分情况下，加锁的代码不仅不存在多线程竞争，而且总是由同一个线程多次获得。所以基于这样一个概率，synchronized 在JDK1.6 之后做了一些优化，为了减少获得锁和释放锁带来的性能开销，引入了偏向锁、轻量级锁的概念
因此在 synchronized 中，锁存在四种状态分别是：无锁、偏向锁、轻量级锁、重量级锁。 锁的状态根据竞争激烈的程度从低到高不断升级

偏向锁的基本原理
前面说过，大部分情况下，锁不仅仅不存在多线程竞争，而是总是由同一个线程多次获得，为了让线程获取锁的代价更低就引入了偏向锁的概念。怎么理解偏向锁呢？
当一个线程访问加了同步锁的代码块时，会在对象头中存储当前线程的 ID，后续这个线程进入和退出这段加了同步锁的代码块时，不需要再次加锁和释放锁。而是直接比较对象头里面是否存储了指向当前线程的偏向锁。如果相等表示偏向锁是偏向于当前线程的，就不需要再尝试获得锁了
也就是说偏向锁连CAS操作都不需要

偏向锁的获取和撤销逻辑

1. 首先获取锁 对象的 Markword，判断是否处于未偏向状态。（biased_lock=1、且 ThreadId 为空）
2. 如果是未偏向状态，则通过 CAS 操作，把当前线程的 ID写入到 MarkWord
   a) 如果 cas 成功，那么 markword会记录当前线程id。表示已经获得了锁对象的偏向锁，接着执行同步代码块
   b) 如果 cas 失败，说明有其他线程已经获得了偏向锁，这种情况说明当前锁存在竞争，需要撤销已获得偏向锁的线程，并且把它持有的锁升级为轻量级锁（这个操作需要等到全局安全点，也就是没有线程在执行字节码时）才能执行
3. 如果是已偏向状态，需要检查 markword 中存储的ThreadID 是否等于当前线程的 ThreadID
   a) 如果相等，不需要再次获得锁，可直接执行同步代码块
   b) 如果不相等，说明当前锁偏向于其他线程，需要撤销偏向锁并升级到轻量级锁

偏向锁的撤销
偏像锁的撤销是直接将原获得偏向锁的线程升级到轻量级锁，也就是给markWord添加指向栈中锁记录的指针

偏向锁的撤销并不是把对象恢复到无锁可偏向状态（因为偏向锁并不存在锁释放的概念），而是直接把被偏向的锁对象升级到被加了轻量级锁的状态
对原持有偏向锁的线程进行撤销时，原获得偏向锁的线程有两种情况：

1. 原获得偏向锁的线程如果已经退出了临界区，也就是同步代码块执行完了，那么这个时候会把对象头设置成无锁状态并且争抢锁的线程可以基于 CAS 重新设置偏向锁
2. 如果原获得偏向锁的线程的同步代码块还没执行完，处于临界区之内，这个时候会把原获得偏向锁的线程升级为轻量级锁后继续执行同步代码块

在我们的应用开发中，绝大部分情况下一定会存在 2 个以上的线程竞争，那么如果开启偏向锁，反而会提升获取锁的资源消耗。所以可以通过 jvm 参数UseBiasedLocking 来设置开启或关闭偏向锁

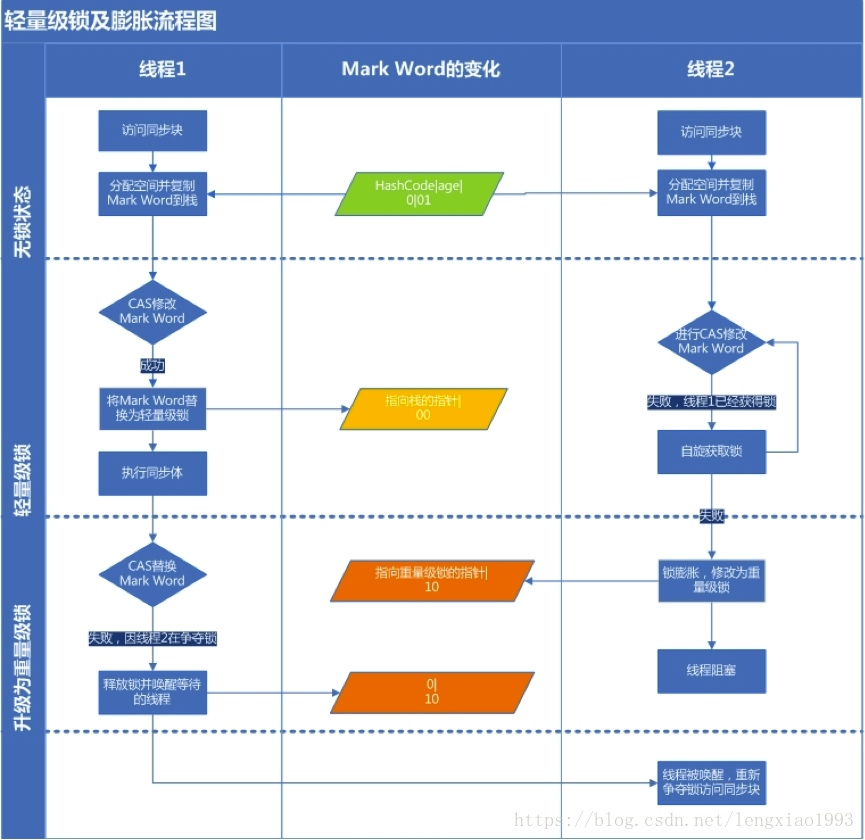
流程图分析

轻量级锁使用的是自旋锁，加锁操作是CAS操作

轻量级锁的加锁逻辑
锁升级为轻量级锁之后，对象的 Markword 也会进行相应的变化。升级为轻量级锁的过程：

1. 线程在自己的栈桢中创建锁记录 LockRecord
2. 将锁对象的对象头中的Mark Word复制到线程的刚刚创建的锁记录中
3. 将锁记录中的 Owner 指针指向锁对象
4. 将锁对象的对象头的 MarkWord替换为指向锁记录的指针

锁对象中的Mark Word指向线程的栈中创建的锁记录LockRecord，LockRecord中的owner指针指向锁对象，就像对象的相互依赖

轻量级锁的实现

• 自旋锁
  轻量级锁在加锁过程中，用到了自旋锁。所谓自旋，就是指当有一个线程去竞争锁时，如果获取不到锁，这个线程会在原地循环等待，而不是把该线程给阻塞，直到持有锁的线程释放锁之后，这个线程就可以马上获得锁

**注意：**锁在原地循环的时候，是会消耗 cpu 的，就相当于在执行一个啥也没有的 for 循环。所以，轻量级锁适用于那些同步代码块执行的很快的场景，这样，线程原地等待很短的时间就能够获得锁了

但是自旋必须要有一定的条件控制，否则如果一个线程执行同步代码块的时间很长，那么这个线程不断的循环反而会消耗 CPU 资源。默认情况下自旋的次数是 10 次，可以通过 preBlockSpin 来修改

自适应自旋锁
自适应意味着自旋的次数不是固定不变的，而是根据前一次在同一个锁上自旋的时间以及锁的拥有者的状态来决定。如果在同一个锁对象上，自旋等待刚刚成功获得过锁，并且持有锁的线程正在运行中，那么虚拟机就会认为这次自旋也是很有可能再次成功，进而它将允许自旋等待持续相对更长的时间。
如果对于某个锁，自旋很少成功获得过，那在以后尝试获取这个锁时将可能省略掉自旋过程，直接阻塞线程，避免浪费处理器资源

轻量级锁的锁膨胀
轻量级锁的锁释放逻辑其实就是获得锁的逆向逻辑，通过CAS 操作把线程栈帧中的 LockRecord 替换回到锁对象的MarkWord 中，如果成功表示没有竞争。如果失败，表示当前锁存在竞争，那么轻量级锁就会膨胀成为重量级锁

轻量级锁膨胀的方式：
（1）设置自旋一定次数
（2）自旋自适应

重量级锁的基本原理

为什么叫重量级锁？
因为重量级锁依赖操作系统的 MutexLock(互斥锁)来实现, 线程被阻塞后便进入内核（Linux）调度状态，这个会导致系统在用户态与内核态之间来回切换，严重影响锁的性能

当轻量级锁膨胀到重量级锁之后，意味着线程获取锁失败之后只能被挂起进入一个同步队列，处于阻塞状态来等待被唤醒了

每一个 JAVA 对象都会与一个监视器 monitor 关联，我们可以把它理解成为一把锁，当一个线程想要执行一段被synchronized 修饰的同步方法或者代码块时，该线程得先获取到 synchronized 修饰的对象对应的 monitor。
monitor.enter 表示去获得一个对象监视器。monitor.exit 表示释放 monitor 监视器的所有权，使得其他被阻塞的线程可以尝试去获得这个监视器

重量级锁加锁的流程

任意线程对 Object（Object 由 synchronized 保护）的访问，首先要获得 Object 的监视器。如果获取失败，线程进入同步队列，线程状态变为 BLOCKED。当获得了锁的线程释放了锁，则该释放操作唤醒阻塞在同步队列中的线程，使其重新尝试对监视器的获取。

回顾线程的竞争机制
再来回顾一下线程的竞争机制对于锁升级这块的一些基本流程。假如有这样一个同步代码块，存在 Thread#1、Thread#2 等多个线程

synchronized (lock) {
// do something
}

情况一：只有 Thread#1 会进入临界区；
情况二：Thread#1 和 Thread#2 交替进入临界区,竞争不激烈；
情况三：Thread#1/Thread#2/Thread3… 同时进入临界区，竞争激烈

偏向锁
当 Thread#1 进入临界区时，JVM 会将 lockObject 的对象头 Mark Word 的锁标志位设为“01”，同时会用 CAS 操作把 Thread#1 的线程 ID 记录到 Mark Word 中，此时进入偏向锁模式。所谓“偏向”，指的是这个锁会偏向于 Thread#1，若接下来没有其他线程进入临界区，则 Thread#1 再出入临界区无需再执行任何同步操作
也就是说，若只有Thread#1 会进入临界区，实际上只有其初次进入临界区时需要执行 CAS 操作，以后再出入临界区都不会有同步操作带来的开销

轻量级锁
偏向锁的场景过于理想化，更多的时候会存在 Thread#2 也会尝试进入临界区， 如果 Thread#2 也进入临界区但是Thread#1 还没有执行完同步代码块时，会暂停 Thread#1并且升级到轻量级锁。Thread#2 通过自旋再次尝试以轻量级锁的方式来获取锁

重量级锁
如果 Thread#1 和 Thread#2 正常交替执行，那么轻量级锁基本能够满足锁的需求。但是如果 Thread#1 和 Thread#2同时进入临界区，那么轻量级锁就会膨胀为重量级锁，意味着 Thread#1 线程获得了重量级锁的情况下，Thread#2就会被阻塞

借鉴一张网上比较整理的比较全面的各种锁状态转换的流程图：