机器学习之数学基础一 .导数

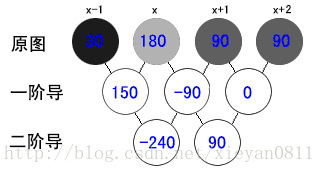
简单的说,导数是曲线的斜率,是曲线变化快慢的反应.

2阶导数是斜率变化快慢的反应,反应曲线的凸凹性

例如:加速度的方向总是指向轨迹曲线凹的一侧.

导数(Derivative)是微积分学中重要的基础概念.一个函数在某一点的导数描述了这个函数在这一点附近的变化率.导数的本质是通过极限的概念对函数进行局部的线性逼近.当函数f的自变量在一点x0上产生一个增量h时,函数输出值的增量与自变量增量h的比值在h趋于0时的极限存在，即为f在x0处的导数, 记作 $f'(x_0)$ 、 $\frac{\mathrm{d}f}{\mathrm{d}x}(x_0)$ 或 $\left.\frac{\mathrm{d}f}{\mathrm{d}x}\right|_{x=x_0}$ .

例: 在运动学中,物体的位移对于时间的导数就是物体的瞬时速度.

导数是函数的局部性.不是所有的函数都有导数,一个函数也不一定在所有的点上都有导数,若函数在某一点函数存在,则称其为在这一点可导,否则称为不可导,如果函数的自变量和取值都是实数的话，那么函数在某一点的导数就是该函数所代表的曲线在这一点上的切线斜率。

对于可导的函数 $f$ ， $x \mapsto f'(x)$ 也是一个函数，称作 $f$ 的导函数。寻找已知的函数在某点的导数或其导函数的过程称为求导。反之，已知导函数也可以倒过来求原来的函数，即不定积分.

一般定义

设有定义域和取值都在实数域中的函数 $y=f(x)\;$ 。若 $f(x)\;$ 在点 $\;x_0\;$ 的某个邻域内有定义，则当自变量 $\;x\;$ 在 $\;x_0\;$ 处取得增量 $\Delta x\;$ （点 $\;x_0+\Delta x\;$ 仍在该邻域内）时，相应地 $\;y\;$ 取得增量 $\Delta y=f(x_0+\Delta x)-f(x_0)\,\!$ ；如果 $\Delta \;y\;$ $\Delta \;x\;$ 之比当 $\Delta x\to 0$ 时的极限存在，则称函数 $y=f(x)\,\!$ 在点 $\;x_0\;$ 处可导，并称这个极限为函数 $y=f(x)\,\!$ 在点 $\;x_0\;$ 处的导数，记为 $f'(x_0)\;$ ，

即： $f'(x_0)=\lim_{\Delta x \to 0}\frac{\Delta y}{\Delta x}=\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

也可记作 $y^\prime (x_0)$ 、 $\left.\frac{\mathrm{d}y}{\mathrm{d}x}\right|_{x=x_0}$ 、 $\frac{\mathrm{d}f}{\mathrm{d}x}(x_0)$ 或 $\left.\frac{\mathrm{d}f}{\mathrm{d}x}\right|_{x=x_0}$ 。

导数、导函数与微分算子

若函数 $\;f(x)\;$ 在其定义域包含的某区间 $\;I\;$ 内每一个点都可导，那么也可以说函数 $\;f(x)\;$ 在区间 $\;I\;$ 内可导，这时对于 $\;I\;$ 内每一个确定的 $\;x\;$ 值，都对应着 $\;f\;$ 的一个确定的导数值，如此一来就构成了一个新的函数 $x \mapsto f'(x)$ ，这个函数称作原来函数 $\;f(x)\;$ 的导函数，记作： $\;y'\;$ 、 $f'(x)\;$ 或者 ${\tfrac {{\mathrm {d}}f}{{\mathrm {d}}x}}(x)$ 。值得注意的是，导数是一个数，是指函数 $f(x)\;$ 在点 $x_0\;$ 处导函数的函数值。但在不至于混淆的情况下，通常也可以说导函数为导数。

由于对每一个可导的函数 $\;f(x)\;$ ，都有它的导函数 $f'(x)\;$ 存在，我们还可以定义将函数映射到其导函数的算子。这个算子称为微分算子，一般记作 $D$ 或 ${\tfrac {{\mathrm {d}}}{{\mathrm {d}}x}}$ 。例如：

$\begin{align} D(x \mapsto 1) &= (x \mapsto 0)\\ D(x \mapsto x) &= (x \mapsto 1)\\ D(x \mapsto x^2) &= (x \mapsto 2\cdot x) \end{align}$

由于微分算子的输出值仍然是函数，可以继续求出它在某一点的取值。比如说对于函数 $\;f(x)=x^2\;$ ， $D(f) = (x \mapsto 2 \cdot x)$

所以 $D(f)(x) = 2x$ ， $D(f)(1.4) = 2 \times 1.4 = 2.8$ 。

导数与微分

微分也是一种线性描述函数在一点附近变化的方式。微分和导数是两个不同的概念。但是，对一元函数来说，可微与可导是完全等价的。可微的函数，其微分等于导数乘以自变量的微分 $\mathrm{d}x$ ，换句话说，函数的微分与自变量的微分之商等于该函数的导数。因此，导数也叫做微商。函数 $y = f(x)$ 的微分又可记作 $\mathrm{d}y = f'(x)\mathrm{d}x$ 。

函数可导的条件

如果一个函数的定义域为全体实数，即函数在 $(-\infty,+\infty)$ 上都有定义，那么该函数是不是在定义域上处处可导呢？答案是否定的。函数在定义域中一点可导需要一定的条件。首先，要使函数 $f$ 在一点可导，那么函数一定要在这一点处连续。换言之，函数若在某点可导，则必然在该点处连续。这个结论来自于连续性的定义。

然而，连续性并不能保证可导性。即使函数在一点上连续，也不一定就在这一点可导。事实上，存在着在每一点都连续，但又在每一点都不可导的“病态函数”。1931年，斯特凡·巴拿赫甚至证明，事实上“绝大多数”的连续函数都属于这种病态函数（至少在一点可导的连续函数在所有连续函数中是贫集）。在连续而不可导的函数里，一种常见的情况是，函数在某一点连续，并且可以定义它的左导数和右导数：

左导数： $f'_{-}(x_0)=\lim_{\Delta x \to 0^{-}}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

右导数： $f'_{+}(x_0)=\lim_{\Delta x \to 0^{+}}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

然而左导数和右导数并不相等，因而函数在该处不可导。

实际上，若函数导数存在，则必然可以推出左右导数相等，这是由极限的性质（极限存在则左右极限相等）得来：

$\lim_{\Delta x \to 0}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} =\lim_{\Delta x \to 0^{-}}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x} =\lim_{\Delta x \to 0^{+}}\frac{f(x_0+\Delta x)-f(x_0)}{\Delta x}$

单调性

根据微积分基本定理，对于可导的函数 $f$ ，有： $f(b) - f(a) = \int^b_a f'(t)\mathrm{d}t$

如果函数的导函数在某一区间内恒大于零（或恒小于零），那么函数在这一区间内单调递增（或单调递减），这种区间也称为函数的单调区间。导函数等于零的点称为函数的驻点（或极值可疑点），在这类点上函数可能会取得极大值或极小值。进一步判断则需要知道导函数在附近的符号。对于满足 $f'(x_0) = 0$ 的一点 $x_{0}$ ，如果存在 $\delta > 0$ 使得 $f'$ 在区间 $(x_0 - \delta, x_0]$ 上都大于等于零，而在区间 $[x_0 , x_0 + \delta)$ 上都小于等于零，那么 $x_{0}$ 是一个极大值点，反之则为极小值点。

如果 $f''(x_{0})=0$ 并且 $f''(x)$ 在 $x_{0}$ 改变加减号，则称这个点是拐点；否则这个点不是拐点。

如果函数在 $x_{0}$ 处的二阶导数 $f''(x_0)$ 存在，极值点也可以用它的正负性判断（已确定 $f'(x_0)=0$ ）。如果 $f''(x_0) > 0$ ，那么 $x_{0}$ 是一个极小值点，反之为极大值点。

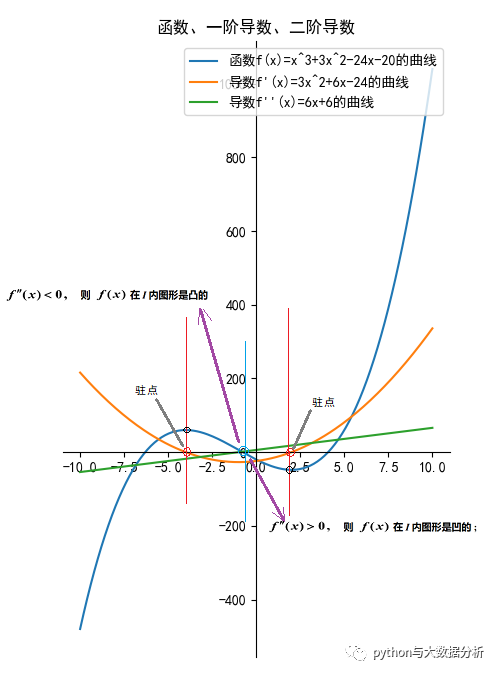
凹凸性

可导函数的凹凸性与其导数的单调性有关。如果函数的导函数在某个区间上单调递增，那么这个区间上函数是向下凸的，反之则是向上凸的。如果二阶导函数存在，也可以用它的正负性判断，如果在某个区间上 $f''$ 恒大于零，则这个区间上函数是向下凸的，反之这个区间上函数是向上凸的.

基本函数的导数

如果 $\scriptstyle f(x) = x^r\,$ ，其中 $r$ 是非零实数，那么导函数 $\scriptstyle f'(x) = rx^{r-1}\,$ 。函数 $f$ 的定义域可以是整个实数域，但导函数的定义域则不一定与之相同,例如当 $r = \frac{1}{2}$ 时： $f'(x) = \frac{1}{2}x^{-\tfrac12}\,$
底数为 $e$ 的指数函数 $\scriptstyle y = e^x$ 的导数还是自身： $\scriptstyle \frac{\mathrm{d}}{\mathrm{d}x}e^x = e^x.$
而一般的指数函数 $y = a^x$ 的导数还需要乘以一个系数： $\scriptstyle \frac{\mathrm{d}}{\mathrm{d}x}a^x = \ln(a)a^x.$

函数	原函数	导函数
常函数（即常数）	（C为常数）
指数函数
幂函数
对数函数
正弦函数
余弦函数
正切函数
余切函数
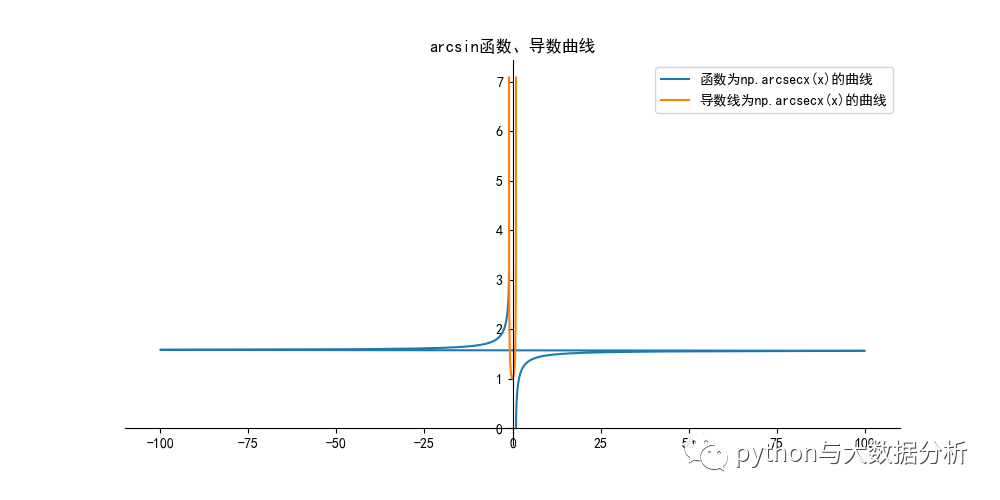
正割函数
余割函数
反正弦函数
反余弦函数
反正切函数
反余切函数
双曲线函数

1、导数的四则运算：

2、原函数与反函数导数关系（由三角函数导数推反三角函数的）：

y=f（x）的反函数是x=g（y），则有y'=1/x'。

3、复合函数的导数：

复合函数对自变量的导数，等于已知函数对中间变量的导数，乘以中间变量对自变量的导数（称为链式法则）。

4、变限积分的求导法则：

（a（x）,b（x）为子函数）

偏导数

如果有函数 $f$ 其自变量不是单个实数，而是多于一个元素，例如： $f(x,y) = x^2 + xy + y^2.\,$

这时可以把其中一个元素（比如 $x$ ）看做参数，那么 $f$ 可以看做是关于另一个元素的参数函数： $f(x,y) = f_x(y) = x^2 + xy + y^2.\,$

也就是说，对于某个确定的 $x$ ，函数 $f_x$ 就是一个关于 $y$ 的函数。在 $x=a$ 固定的情况下，可以计算这个函数 $f_x$ 关于 $y$ 的导数。 $f_a'(y) = a + 2y\,$

这个表达式对于所有的 $a$ 都对。这种导数称为偏导数，一般记作： ${\frac {\partial f}{\partial y}}(x,y)=x+2y$

这里的符号 ∂ 是字母 $d$ 的圆体变体，一般读作 $\delta$ 的首音节或读“偏”，以便与 $d$ 区别。

更一般地来说，一个多元函数 $f \left( x_1 , x_2 , \cdots, x_n \right)$ 在点 $\left( a_1 , a_2 , \cdots, a_n \right)$ 处对 $x_{i}$ 的偏导数定义为：

${\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n})=\lim _{h\to 0}{\frac {f(a_{1},\ldots ,a_{i}+h,\ldots ,a_{n})-f(a_{1},\ldots ,a_{n})}{h}}.$

上面的极限中，除了 $x_{i}$ 外所有的自变元都是固定的，这就确定了一个一元函数：

$f_{a_1,\ldots,a_{i-1},a_{i+1},\ldots,a_n}(x_i) = f(a_1,\ldots,a_{i-1},x_i,a_{i+1},\ldots,a_n)$

因此，按定义有：

${\frac {df_{a_{1},\ldots ,a_{i-1},a_{i+1},\ldots ,a_{n}}}{dx_{i}}}(a_{i})={\frac {\partial f}{\partial x_{i}}}(a_{1},\ldots ,a_{n}).$

偏导数的实质仍然是一元函数的导数。

多变量函数的一个重要的例子，是从 $\mathbf{R}^n$ （例如 $\mathbf{R}^2$ 或 $\mathbf{R}^3$ ）映射到 $\mathbf{R}$ 上的标量值函数 $f \left( x_1 , x_2 , \cdots, x_n \right)$ 。在这种情况下， $f$ 关于每一个变量 $x_{i}$ 都有偏导数 ${\frac {\partial f}{\partial x_{i}}}$ 。在点 $x=\boldsymbol{a}$ ，这些偏导数定义了一个向量：

$\nabla f({\boldsymbol {a}})=\left[{\frac {\partial f}{\partial x_{1}}}({\boldsymbol {a}}),\ldots ,{\frac {\partial f}{\partial x_{n}}}({\boldsymbol {a}})\right]$ 。