决策树后剪枝算法(一)代价复杂度剪枝CPP
决策树后剪枝算法(二)错误率降低剪枝REP
决策树后剪枝算法(三)悲观错误剪枝PEP
决策树后剪枝算法(四)最小错误剪枝MEP
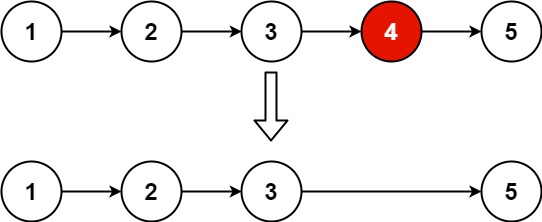
剪枝,是一个“用准确性换取简单性”的思想。它允许决策树对训练集过拟合,再通过删除对泛化精度无贡献的子分支,从而修剪出一颗较小的树。以下列出几种较常见的后剪枝算法,及其机制对比:
| CCP | REP | PEP | MEP | |
|---|---|---|---|---|
| 剪枝方式 | 自底向上 | 自底向上 | 自顶向下 | 自底向上 |
| 计算复杂度 | O ( n 2 ) O(n^2) O(n2) | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) | O ( n ) O(n) O(n) |
| 误差估计 | 标准误差 | 剪枝集上误差 | 连续性矫正 | 概率估计 |
| 是否需要额外剪枝集 | 否 | 是 | 否 | 否 |
(1)代价复杂度剪枝(CCP)
CCP算法为子树 T t T_t Tt定义了代价和复杂度,以及一个衡量代价与复杂度之间关系的参数 α \alpha α。大致流程为,从决策树 T 0 T_0 T0开始不断剪枝直到 T 0 T_0 T0的根节点,形成一个子树序列{ T 0 , T 1 , . . . , T n T_0, T_1,...,T_n T0,T1,...,Tn}; 然后经过交叉验证法在独立验证集上逐个测试评估, 从而选出最优子树。
(1.1)数学推导
评价标准:
R α ( T ) = R ( T ) + α ∣ f ( T ) ∣ R ( T ) = ∑ t ∈ f ( T ) r ( t ) . p ( t ) = ∑ t ∈ f ( T ) R ( t ) R_\alpha(T) = R(T) + \alpha|f(T)|\\ R(T)=\sum_{t\in f(T)}r(t).p(t)=\sum_{t\in f(T)}R(t) Rα(T)=R(T)+α∣f(T)∣R(T)=t∈f(T)∑r(t).p(t)=t∈f(T)∑R(t)
解读:
- R α ( T ) R_{\alpha}(T) Rα(T)即为一棵树好坏的评价标准。
- R ( T ) R(T) R(T)是决策树训练集误差(代价), ∣ f ( T ) ∣ |f(T)| ∣f(T)∣表示决策树的叶子节点数量(复杂度)。
- α \alpha α是正则化参数,用以权衡训练数据的拟合程度与模型复杂度。
- ∑ t ∈ f ( T ) R ( t ) \sum_{t\in f(T)}R(t) ∑t∈f(T)R(t)表示每个叶子节点所产生的错误分类的误差和。
- p ( t ) p(t) p(t)为叶子节点权重( = n ( t ) n =\frac{n(t)}{n} =nn(t)), r ( t ) r(t) r(t)为叶子结点误分类率( = e r r o r ( t ) n ( t ) =\frac{error(t)}{n(t)} =n(t)error(t))。
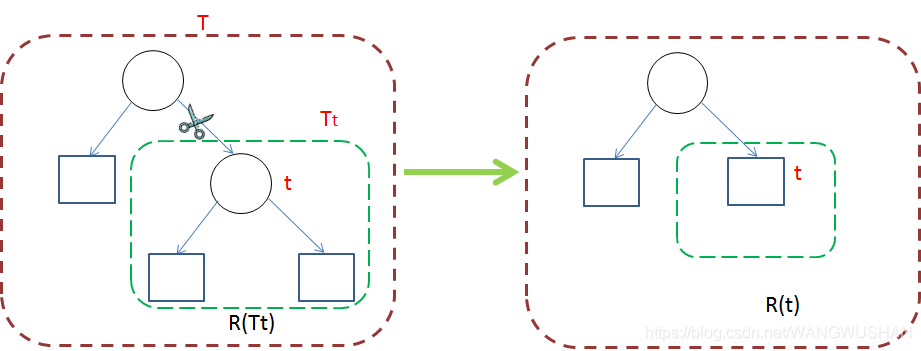
进一步推导,对于一个固定的 α \alpha α值, 一定存在一颗使得 C α ( T ) C_{\alpha}(T) Cα(T)最小的子树 T α T_{\alpha} Tα, 即在固定 α \alpha α下的最优剪枝策略。现在考虑 α \alpha α变化,考虑极端情况: 当 α = 0 \alpha=0 α=0时, 有 R α ( T ) = R ( T ) R_\alpha(T) = R(T) Rα(T)=R(T), 即不考虑复杂度, 易知完整树即为最优;当 α → ∞ \alpha\rightarrow\infty α→∞,复杂度权重无穷大,易知单节点树为最优。及 α \alpha α从 0 → ∞ 0\rightarrow\infty 0→∞, α \alpha α对应的最优树 T α T_{\alpha} Tα从繁变简。
再结合 B r e i m a n Breiman Breiman等人的证明: 将 α \alpha α从小增大, 0 = α 0 < α 1 < . . . < α n < ∞ 0=\alpha_0<\alpha_1<...<\alpha_n<\infty 0=α0<α1<...<αn<∞, 产生一系列的区间 [ a i , a i + 1 ) [a_i, a_{i+1}) [ai,ai+1), i = 0 , 1 , 2 , . . . , n i=0,1,2,...,n i=0,1,2,...,n; 剪枝得到的子树序列对应着区间 α ∈ [ a i , a i + 1 ) , i = 0 , 1 , 2... n \alpha\in{[a_i, a_{i+1})},~i=0,1,2...n α∈[ai,ai+1), i=0,1,2...n的最优子树序列{ T 0 , T 1 , . . . , T n T_0, T_1, ...,T_n T0,T1,...,Tn},序列中的子树是嵌套的, 即 T 0 T_0 T0爷爷/ T 1 T_1 T1父亲/ T 2 T_2 T2儿子/ T 3 T_3 T3孙子…以此类推。
那么如何选取每一阶段的 α \alpha α, 这里引入剪枝整体损失函数减少程度指标 g ( t ) = R ( t ) − R ( T t ) ∣ T t ∣ − 1 g(t)=\frac{R(t)-R(T_t)}{|T_t|-1} g(t)=∣Tt∣−1R(t)−R(Tt),其具体含义如下:
当 R α ( T t ) = R α ( t ) 时 , 即剪枝后误差增长率为 0 R α ( T t ) = R α ( T t ) + ∣ f ( T t ) ∣ R α ( t ) = R α ( t ) + 1 解得 α ’ = R ( t ) − R ( T t ) ∣ T t ∣ − 1 , 即剪枝临界点 ( 必定剪枝 ) 当R_\alpha(T_t)=R_\alpha(t)时,即剪枝后误差增长率为0\\ R_\alpha(T_t)=R_\alpha(T_t)+|f(T_t)|\\ R_\alpha(t)=R_\alpha(t)+1\\ 解得\alpha’=\frac{R(t)-R(T_t)}{|T_t|-1},即剪枝临界点(必定剪枝) 当Rα(Tt)=Rα(t)时,即剪枝后误差增长率为0Rα(Tt)=Rα(Tt)+∣f(Tt)∣Rα(t)=Rα(t)+1解得α’=∣Tt∣−1R(t)−R(Tt),即剪枝临界点(必定剪枝)
且可证得 g ( t ) g(t) g(t)与误差增长率成正比:
KaTeX parse error: Expected 'EOF', got '&' at position 75: …T-T_t)|-|f(T)|)&̲\\ =[R(else)+R(…
根据以上推导结论, 对于特定 α \alpha α区间,要求最优 T α T_\alpha Tα需寻求误差增长率最小, 即 g ( t ) g(t) g(t)最小。故我们所需要做的, 就是每轮迭代中遍历所有非叶子节点, T i − 1 T_{i-1} Ti−1剪枝 g ( t ) g(t) g(t)最小的节点生成下一颗最优子树 T i T_i Ti,从而生成子树序列。
最后基于独立验证集, 对子树序列 T 0 , T 1 , . . . , T n T_0, T_1, ...,T_n T0,T1,...,Tn中的平方误差或基尼系数逐个计算, 再作评估选择即可。
(1.2)算法流程
- 输入:CART算法生成的决策树 T 0 T_0 T0
- 输出:最优决策树 T α T_\alpha Tα
- (1)设 k = 0 , T = T 0 k=0, T=T_0 k=0,T=T0
- (2)设 α = + ∞ \alpha=+\infin α=+∞
- (3)自下而上地对各内部结点 t t t计算 R ( T t ) R(T_t) R(Tt), ∣ f ( T t ) ∣ |f(T_t)| ∣f(Tt)∣以及:
g ( t ) = R ( t ) − R ( T t ) ∣ T t ∣ − 1 α = m i n ( α , g ( t ) ) g(t)=\frac{R(t)-R(T_t)}{|T_t|-1}\\ \alpha=min(\alpha, g(t)) g(t)=∣Tt∣−1R(t)−R(Tt)α=min(α,g(t))
- (4)对 g ( t ) = α g(t)=\alpha g(t)=α的内部结点 t t t进行剪枝, 并对叶结点构成的树,回到步骤(2);否则令 T k = T n T_k=T_n Tk=Tn。
- (7)采用交叉验证法在子树序列 T 0 , T 1 , . . . , T n T_0, T_1, ...,T_n T0,T1,...,Tn中选取最优子树 T α T_\alpha Tα(分类:基尼系数 \ 回归:平均误差)。
(1.3)例题计算
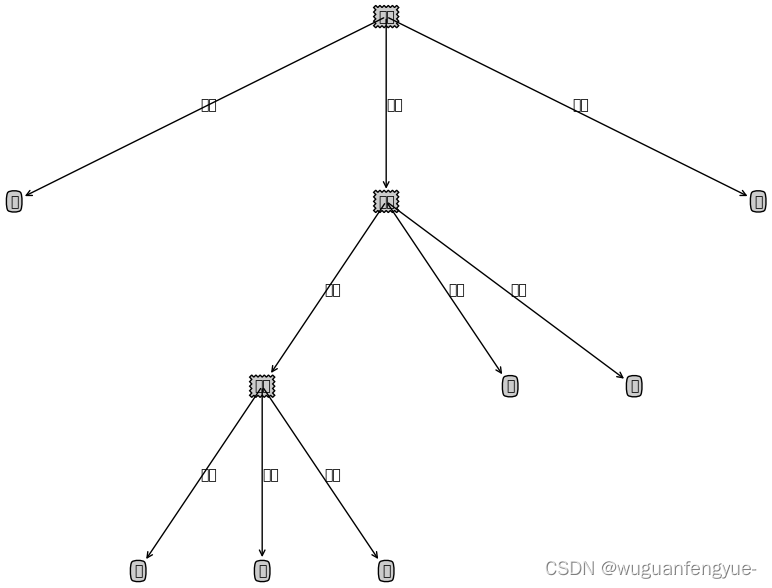
#### (一)原始决策树

#### (二)第一次迭代
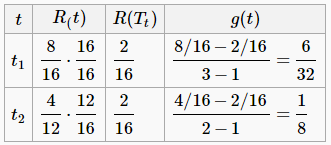
INPUT: α = 0 , T 1 = t 1 , t 2 , t 3 \alpha=0,~ T^1={t_1,t_2,t_3} α=0, T1=t1,t2,t3

OUTPUT: α 2 = min g 1 ( t ) = 1 8 , t = t 2 或 t 3 \alpha^2=\min{g_1(t)}=\frac{1}{8},~t=t_2或t_3 α2=ming1(t)=81, t=t2或t3

#### (三)第二次迭代
INPUT: a l p h a 2 = 1 8 , T 2 = t 1 , t 2 alpha^2=\frac{1}{8},T^2={t_1, t_2} alpha2=81,T2=t1,t2
OUTPUT: α 3 = min g 2 ( t ) = 1 8 , t = t 2 \alpha^3=\min{g_2(t)=\frac{1}{8}}, t=t_2 α3=ming2(t)=81,t=t2

#### (四)第三次迭代
INPUT: T 3 = t 1 T^3={t1} T3=t1
OUTPUT: α 4 = g 3 ( t 1 ) = 8 16 − 4 16 2 − 1 = 1 4 \alpha^4=g_3(t_1)=\frac{\frac{8}{16}-\frac{4}{16}}{2-1}=\frac{1}{4} α4=g3(t1)=2−1168−164=41
即子树序列 T 0 , T 1 , . . . , T n T_0, T_1, ...,T_n T0,T1,...,Tn及其参数 α \alpha α的计算, 接下来进行交叉验证即可选择最优子树即可。
(1.4)代码实现
手写实现 + sklearn实现
链接:https://pan.baidu.com/s/1gskUIAHfv9lZ6Mtq7r7I1Q
提取码:wo7m
代码参考:http://www.hzcourse.com/web/refbook/detail/9970/226
——————————————————————————————————————————-—————————————————
参考资料:
[1] 现代决策树模型及其编程实践 黄智濒 编著
[2] 统计学习方法(第二版) 李航 著
[3] https://blog.csdn.net/WANGWUSHAN/article/details/108556371




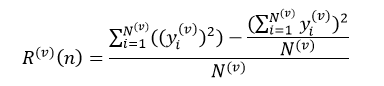



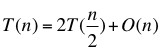


![[算法] 栈和队列](https://img-blog.csdnimg.cn/ce7df0be33f0470fb7d74a4b449cb342.png?x-oss-process=image/watermark,type_d3F5LXplbmhlaQ,shadow_50,text_Q1NETiBA6KW_56eR6IOh5YWI55Sf,size_20,color_FFFFFF,t_70,g_se,x_16)