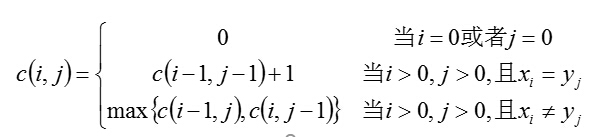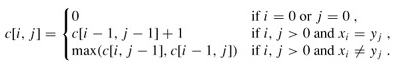三个方法都有所借鉴,但代码部分是自己试着写出来的,虽然最后的运行结果都是正确的,但此过程中难免会有考虑不周全的地方,如发现代码某些地方有误,欢迎指正。同时有新的想法,也可以提出!
采用顺序结构存储串,求串s和串t的一个最长公共子串。
方法一
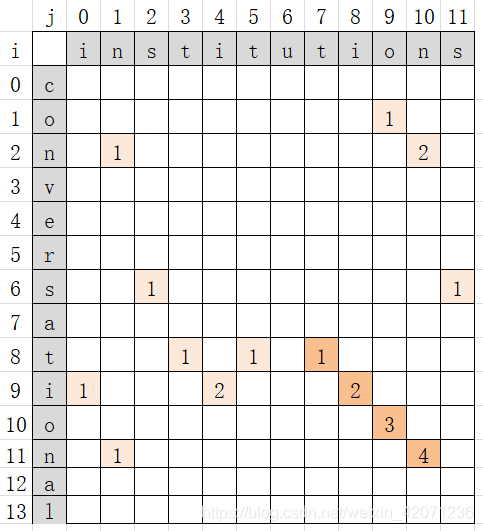
- 算法思想:借助二维数组可以求出最长公共子串最后一个字符分别在s串和t串中的数组下标。此时可以从s中截取最长公共子串,也可以从t中截取。
SqString MaxComStr(SqString s, SqString t)
{SqString str;int arr[MaxSize][MaxSize];int i, j, k, maxi[2], maxlen = 0;for (i = 0; i < s.length; i++)for (j = 0; j < t.length; j++){if (s.data[i] == t.data[j]){if (i == 0 || j == 0) arr[i][j] = 1;else{arr[i][j] = arr[i - 1][j - 1] + 1;if (arr[i][j] > maxlen){maxlen = arr[i][j];maxi[0] = i;maxi[1] = j;}printf("\ni=%d j=%d arr=%d", i, j, arr[i][j]);}}else arr[i][j] = 0;}else arr[i][j] = 0;}printf("\n二维数组中最大值的行号为:%d 列号为:%d\n", maxi[0], maxi[1]);//输出二维数组for (i = 0; i < s.length; i++){for (j = 0; j < t.length; j++)printf("%2d", arr[i][j]);printf("\n");}//求公共子串 代码二选一即可(行号截取/列号截取)/*for (k = maxlen - 1, i = maxi[0]; k >= 0; k--, i--) //用行号从s串中截取{str.data[k] = s.data[i];str.length = maxlen;}*/for (k = maxlen - 1, i = maxi[1]; k >= 0; k--, i--) //用列号从t串中截取{str.data[k] = t.data[i];str.length = maxlen;}//输出strprintf("\n最长公共子串为:");DispStr(str);printf("\n");return str;
}
分析
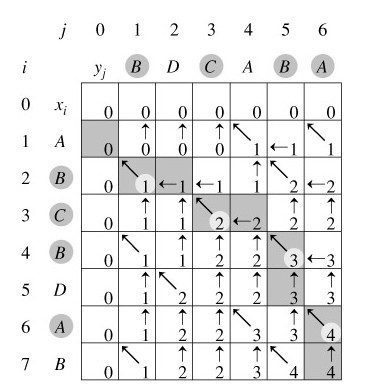
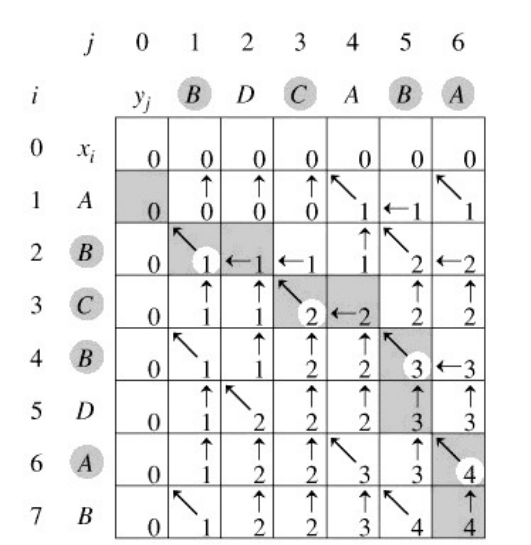
- 分析:LCS (Longest Common Subsequence) 算法
- 构造n×m的二维数组,其中n,m分别为s串和t串的长度。
- 双重循环嵌套,如果s串中的某个字符与t串中的某个字符相等,此时分为两种情况:
①此时相等的字符在二维数组中的第一行或第一列,则将arr[i][j]置为1;
②若是不满足①,则该位置的值为其上左对角线的值+1。即arr[i][j]=arr[i-1][j-1]+1。- 二维数组中的最大值即为最长公共子串的长度,保存它的行、列下标值。
- 若是从s中截取公共子串,则用行号,行号-最长公共子串的长度即得到最长公共子串在s串中的起始下标值;若是从t中截取公共子串,则用列号,列号-最长公共子串的长度即得到最长公共子串在t串中的起始下标值。
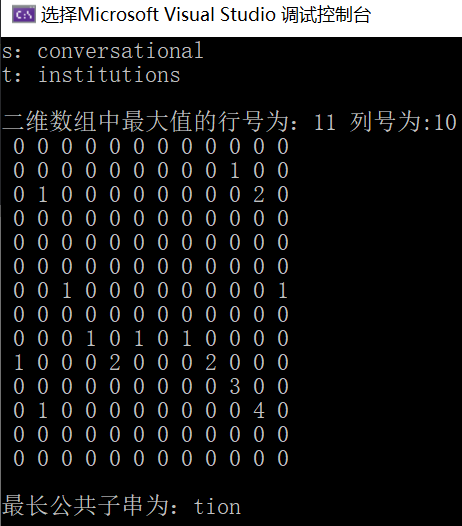
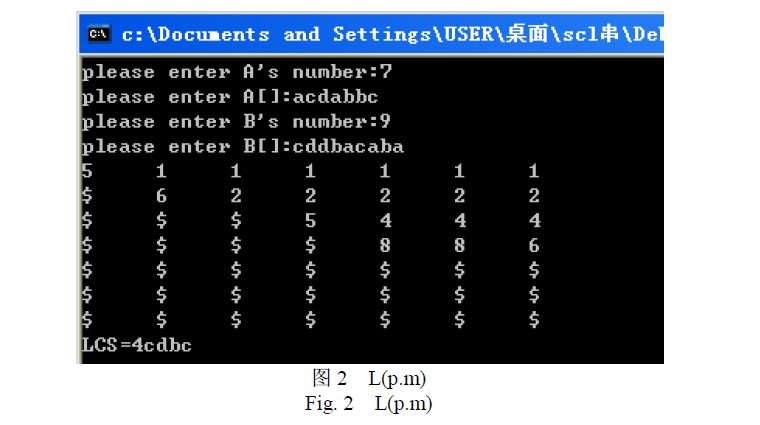
运行结果
- 时间复杂度:O(nm) (主要用在给二维数组赋值)
- 空间复杂度:O(nm) (创建了一个二维数组)
其中n,m分别为s串和t串的长度。
方法二
- 算法思想:采用Brute-Force(暴力)算法,也称简单匹配算法,扫描s串和t串。
SqString MaxComStr(SqString s, SqString t)
{SqString str;int i, j, count = 0, maxlen = 0, start;for (i = 0; i < s.length; i++){for (j = 0; j < t.length; j++){int start1 = i;int start2 = j;while ((start1 <= s.length - 1) && (start2 <= t.length - 1) && (s.data[start1] == t.data[start2])){start1++;start2++;count++;}if (count > maxlen){maxlen = count;start = i;}count = 0;}}printf("\n最长公共子串的起始下标为:%d 子串长度为:%d", start, maxlen);for (i = 0, j = start; i < maxlen; i++, j++)str.data[i] = s.data[j];str.length = maxlen;printf("\n最长公共子串为:");DispStr(str);return str;
}
分析
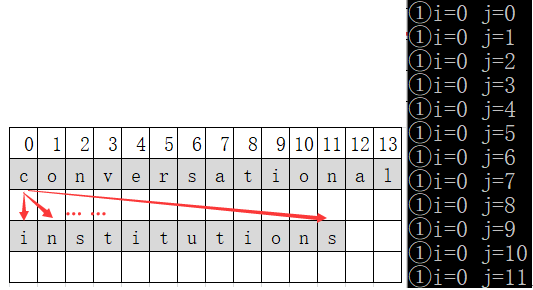
- 串s的data[0](字符’c’)逐个和串t的每个元素进行比较,第一轮没有相同的字符。
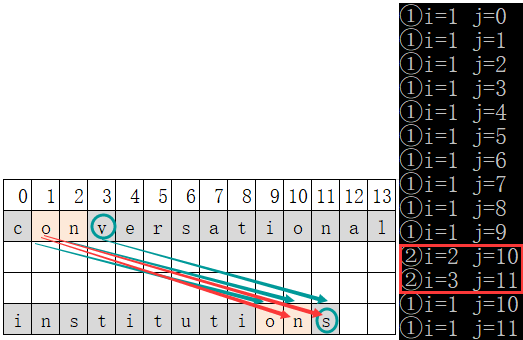
- 串s的data[1](字符’o’)逐个和串t的每个元素进行比较
- ①发现s的data[1]与t中data[9]的字符相等,此时再比较串s和串t的下一个字符(即s的data[2](字符‘n’)与t的data[10](字符’n’)进行比较)。
- ②发现此时两个字符依然相等,再比较两个串的下一个字符(即s的data[3](字符‘v’)与t的data[11](字符’s’)进行比较)。此时发现两个字符不相等,此时串s和串t都不再后移。此轮中有两个字符相等,count=2。
- ③由于①中s.data[1]与t.data[9]已经比较过了,此时让s.data[1](字符’o’)与t.data[10](字符’n’)比较,两个字符不相同,让s.data[1](字符’o’)与t.data[11](字符’s’)比较,两个字符依然不相同。此时t串已到末尾,此轮结束。
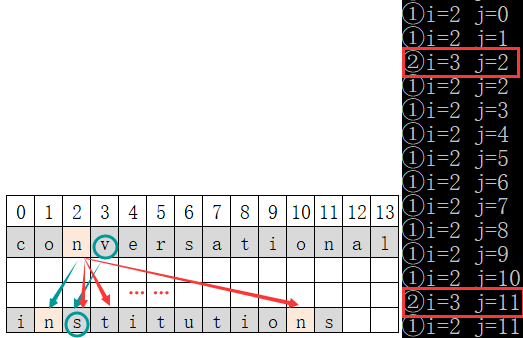
- 串s的data[2](字符’n’)逐个和串t的每个元素进行比较
- ①发现s的data[2]与t中data[1]的字符相等,此时再比较串s和串t的下一个字符(即s的data[3](字符‘v’)与t的data[2](字符’s’)进行比较)。此时发现两个字符不相等,串s和串t都不再后移。
- ②由于①中s.data[2]与t.data[1]已经比较过了,此时让s.data[2](字符’n’)与t.data[2](字符’s’)比较,两个字符不相同,让s.data[2](字符’n’)与t.data[3](字符’t’)比较,两个字符依然不相同,继续此操作。
- ③发现s的data[2]与t中data[10]的字符相等,此时再比较串s和串t的下一个字符(即s的data[3](字符‘v’)与t的data[11](字符’s’)进行比较)。此时发现两个字符不相等,串s和串t都不再后移。
- ④由于③中s.data[2]与t.data[10]已经比较过了,此时让s.data[2](字符’n’)与t.data[11](字符’s’)比较,两个字符不相同,此时t串已到末尾,此轮结束。
运行结果
- 时间复杂度:O(nm) (BF算法的时间复杂度)
- 空间复杂度:O(1) (除了str[ ],未开辟新空间)
其中n,m分别为s串和t串的长度。
方法三
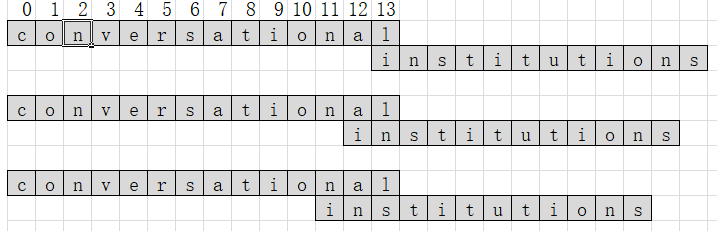
- 算法思想:将较短串的头部和长串的尾部对齐,逐渐移动短串,比较重叠部分的字符串中的最长公共子串的长度,直到短串和长串的头部对齐。
SqString MaxComStr(SqString s, SqString t)
{SqString str;int i = 0, j, k, n = 1, m = s.length;int count = 0, index[2] = {0,0}, num = 0;while (n<=s.length) //循环的轮数由长串决定{i = --m; //每趟比较开始时,长串的起始下标j = 0; //每趟比较开始,短串的起始下标都为0if (i > s.length - t.length) k = s.length - i; //如果短串尾和长串尾没对其,每趟中需要比较的次数依次递增else k=t.length; //一旦短串尾和长串尾对其,之后的每一趟,比较次数都由短串决定while (k > 0) //k为每趟中需要比较次数{if (s.data[i] == t.data[j]) count++; //如果纵向对应的两个字符相等,公共子串的长度+1i++; j++; //依次比较每个纵向对应的两个字符if (s.data[i-1]==t.data[j-1]&&s.data[i] != t.data[j]) //如果前一个纵向的两个字符相等,但下一个纵向的两个字符不相等,即字符不连续相等{if (count > num) //记录最长的连续公共字符{num = count; //记录断开前的最长公共子串的长度index[0] = i - count; //最长公共子串在长串中的起始下标index[1] = index[0] - m; //最长公共子串在短串中的起始下标}count = 0; //每次发现字符不连续相等时,需要重新计数,然后再比较断开前后的长度,取最大值}k--; //每比较一次,剩余需要比较的次数减少}n++; //比较的总趟数减1}for (i = 0, j = index[0]; i < num; i++, j++)str.data[i] = s.data[j];str.length = num;printf("\n最长公共子串在长串中的起始下标为:%d\n在短串中的起始下标为:%d\n最长公共字串的长度为:%d", index[0], index[1], num);printf("\n最长公共子串为:");DispStr(str);return str;
}
分析
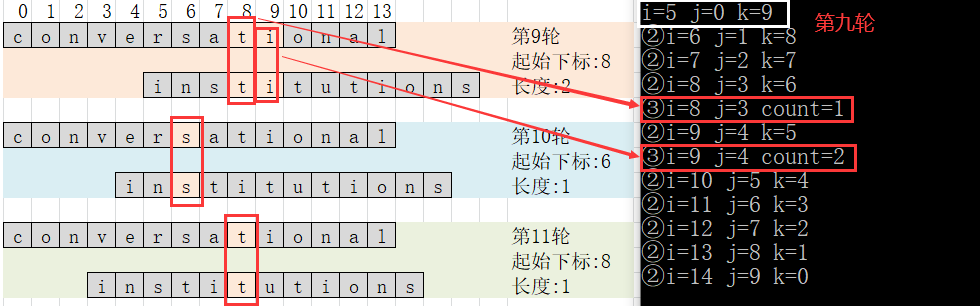
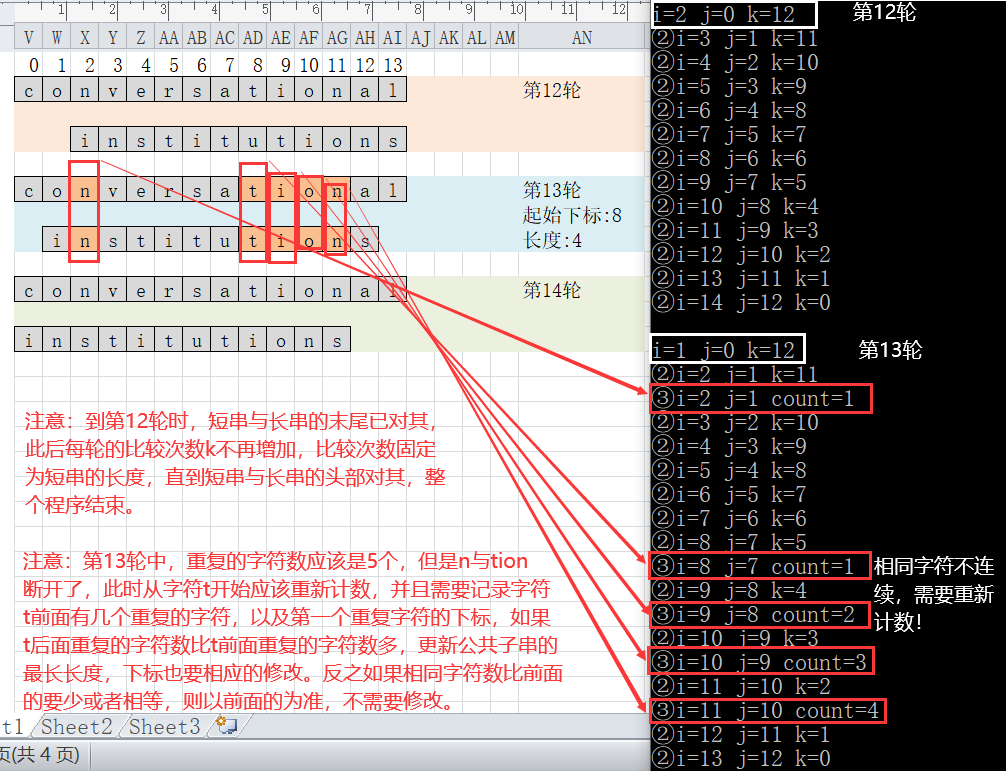
- 该算法只需纵向比较对应位置即可,斜对角的位置可不用比较。
- 如在图中,第二轮比较s.data[12]==t.data[0]?、s.data[13]==t.data[1]?
- 而s.data[12]==t.data[1]?会在下一轮中进行比较;而s.data[13]==t.data[0]?已经在上一轮中比较完毕。
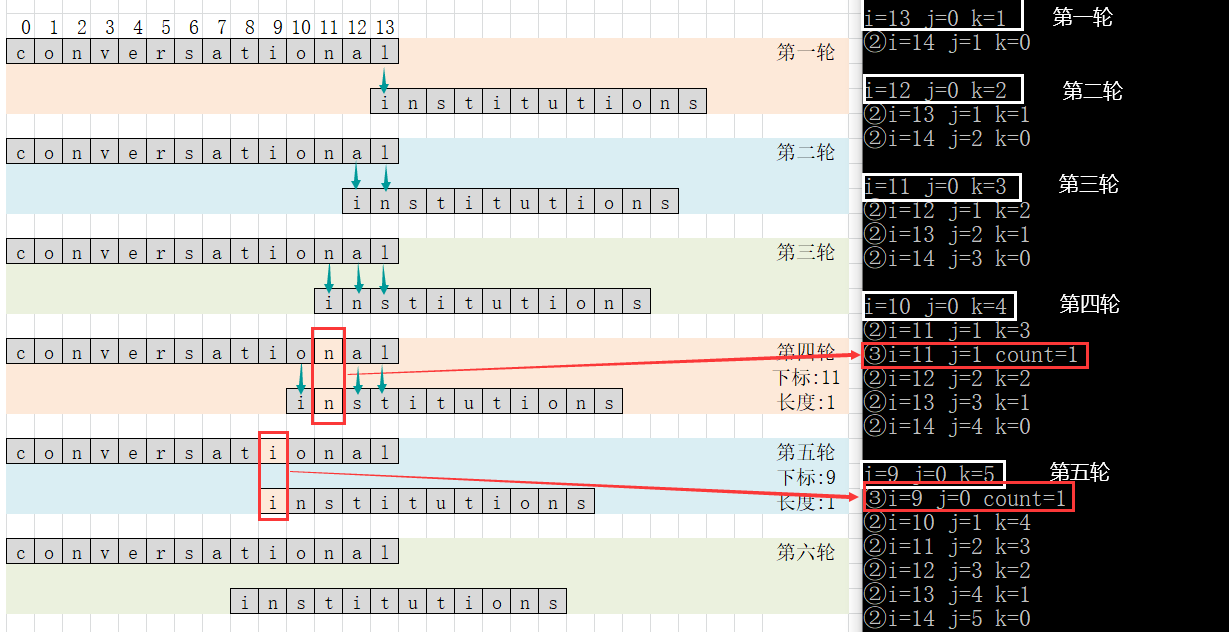
- 从图中可以分析出,总共需要比较14轮(14为较长串的长度),而最坏情况下,第一轮比较1次,第二轮比较2次…第十二轮比较12次(此时两个串尾对齐)。此时离14轮还差两轮,而剩下的两轮比较的次数都是12(即较短串的长度)。
实现步骤:
- 定义一个变量n(用来表示总共需要比较多少轮),比较的轮数由长串的长度决定。每比较一轮,让n++。
- 定义一个变量m(用来表示每一轮中,长串开始比较的起始下标),m的初始值为长串的长度,每一轮中先让m减1之后再开始比较。
- 定义两个变量i(表示每次比较时,长串的起始下标),j(表示每次比较时,短串的起始下标),从图中可以看出,j每次都是比较的范围都是0~m-1,而i可以表示为–m。
- 定义变量k(用来表示每轮循环需要比较次数),每轮比较开始,k=m,每一轮中每比较一次,k–。
- 定义变量count(用来统计每轮中重复字符的个数)
- 定义变量num(最长公共子串的长度)和index(最长公共子串的起始下标)
运行结果
- 时间复杂度: 1 + 2 + . . . + n + ( n − m ) m 1+2+...+n+(n-m)m 1+2+...+n+(n−m)m
- 空间复杂度:O(1)
其中n,m分别为s串和t串的长度。