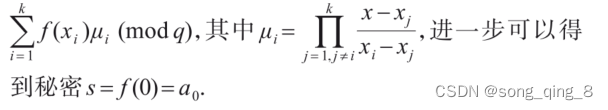1. 引言

Blockstream团队2018年论文《Simple Schnorr Multi-Signatures with Applications to Bitcoin》。
对应的代码实现：
https://github.com/KZen-networks/multi-party-schnorr
https://github.com/lovesh/signature-schemes

论文要点：

• MuSig——new Schnorr-based multi-signature scheme：即一群签名者对同一消息进行联合签名，最终的签名长度要短。
• MuSig方案在plain public-key model下是安全的：即signers are only required to have a public key, but do not have to prove knowledge of the private key corresponding to their public key to some certificate authority or to other signers before engaging the protocol。
• MuSig的主要优势为：
  1）Simple and efficient，具有与标准Schnorr签名相同的key size 和 signature size。
  2）允许key aggregation，即最终的联合签名可采用与标准验签方式类似的方式来验证，使用的是a single “aggregated” public key——可computed from the individual public keys of the signers。
• 提出了a simple (yet non black-box) way to turn the BN multi-signautre scheme into a secure IAS scheme。

1.1 What is Multi-Signature?

Itakura和Nakamura 1983年论文《[A public-key cryptosystem suitable for digital multisignatures]》中首次提出了Multi-Signature概念：
Allow a group of signers (each possessing its own private/public key pair) to produce a single signature $\sigma$ on a message $m$.
Verification of the validity of a purported signature $\sigma$ can be publicly performed given the message and the set of public keys of all signers.

直观的方式是采用标准签名的方式，每个签名者用自己的私钥对消息$m$进行签名，将所有的独立签名拼接在一起。存在的问题是该方式最终产生的签名长度过长，且与签名者数量成正比。

多重签名要求最终的签名长度应与签名者数量无关，且尽量接近标准签名的长度。

1.2 多重签名中的rogue-key attacks

rogue-key attacks即流氓密钥攻击，详见博客 ECDSA VS Schnorr signature VS BLS signature 2.2.2节。

避免rogue-key attacks的方法有：

• 要求签名者prove knowledge of the secret key during public key registration with a certification authority，即knowledge of secret key（KOSK） assumption。该方案存在问题，详情参见[BN06, RY07]。

1.3 What is key aggregation?

Key aggregation是指根据参与多重签名的所有签名者的public keys，生成一个新的aggregated key，利用该aggregated key可对多重签名进行验签。
Key aggregation的好处有：

• a group of $n$ signers want to authorize an action (say, spend some bitcoins) only if all of them agree, but do not necessarily wish to reveal their individual public keys. Then, they can privately compute the aggregated key $\tilde{X}$ corresponding to their multiset of public keys and publish it as an ordinary (non-aggregated) key. Signers are ensured that all of them will need to cooperate to produce a signature which is valid under $\tilde{X}$, whereas verifiers will not even learn that $\tilde{X}$ is in fact an aggregated key.
• aggregated key也可由知道所有public keys的第三方（如someone sending bitcoins to the group of signers）直接计算。

1.5 DL-based多重签名方案对比

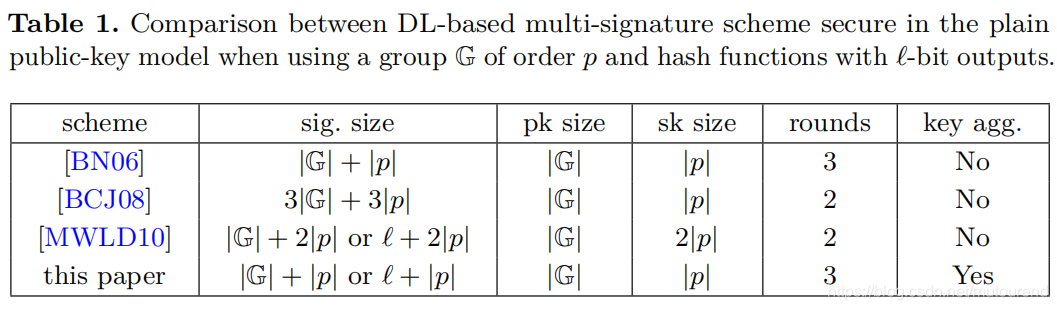
[BCJ08]（2008年论文《Multisignatures Secure Under the Discrete Logarithm Assumption and a Generalized Forking Lemma》）利用了homomorphic commitment scheme，将number of rounds由3减为2，代价是增加了签名的长度以及签名过程和验签过程的计算负担。不支持key aggregation。
[MWLD10]（2010年论文《Efficient discrete logarithm based multi-signature scheme in the plain public key model》）基于Okamoto’s signature机制和double hashing（组合hash，而不是2个hash运算相乘）技术，在保证round数为2的同时，相比于[BCJ08]，减少了签名长度。不支持key aggregation。

1.6 interactive aggregate signature

与多重签名不同，多重签名是对同一消息$m$，由多个签名者进行签名。
当每个签名者has its own message $m_i$时，然后joint signature proves that the $i$-th signer has signed $m_i$，则称为an interactive aggregate signature (IAS) scheme。

IAS schemes are more general than multi-signature schemes, but less flexible than non-interactive aggregate signatures [BGLS03,BNN07] and sequential aggregate signatures [LMRS04].
[BN06] 中指出了a generic (i.e., black-box) way to turn any multi-signature scheme an IAS scheme：
the signers simply run the multi-signature protocol using as message the tuple of all public key/message pairs involved in the IAS protocol.

1.7 Musig的优点

详细参见博客 ECDSA VS Schnorr signature VS BLS signature。。
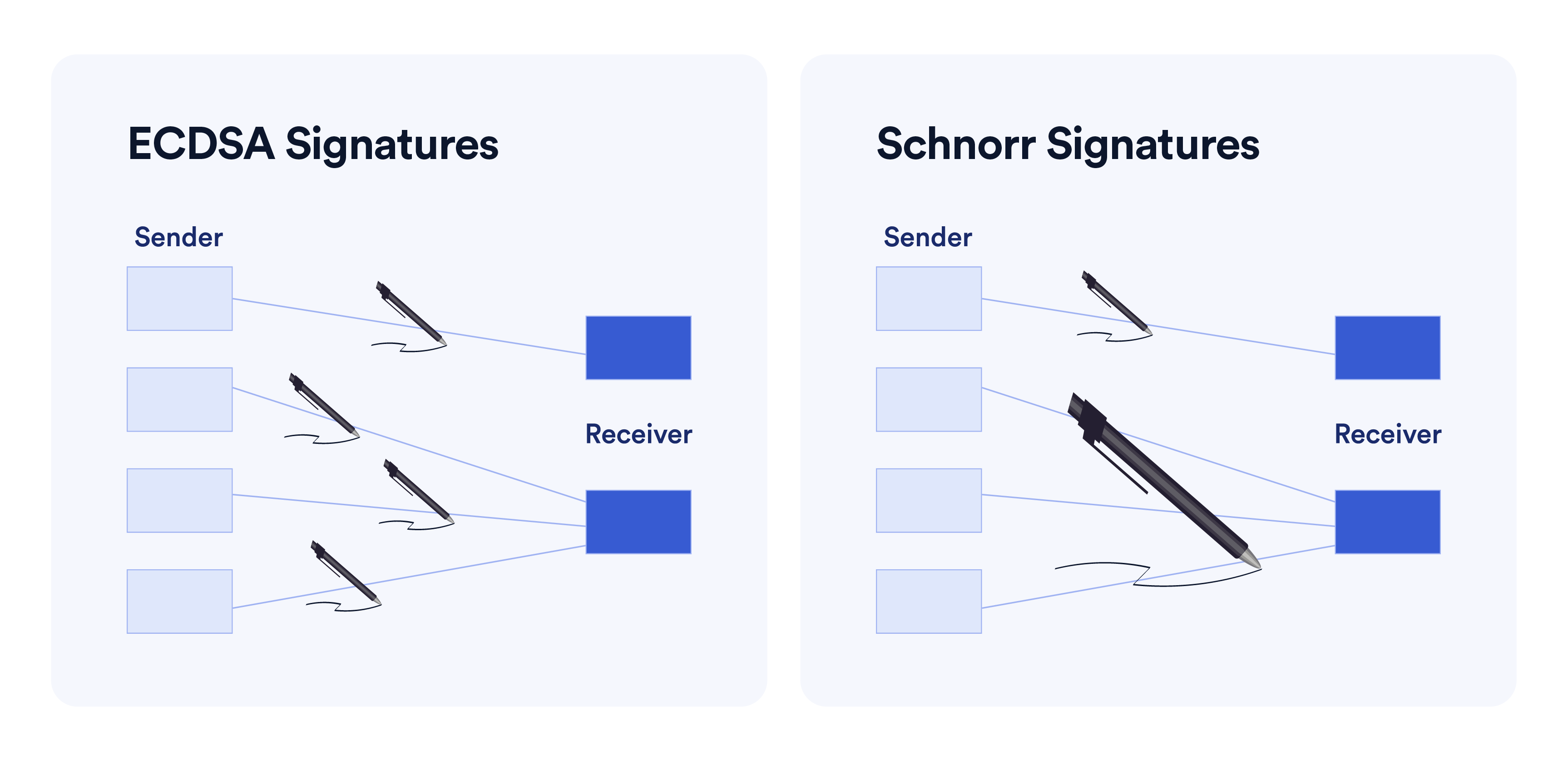
相比于Bitcoin现在采用的ECDSA签名方案，基于Schnorr signature的Musig具有以下两个优点：

• The availability of key aggregation removes the need for verifiers to see all the involved keys, improving bandwidth, privacy, and validation cost.
• Security under the plain public-key model enables multi-signature across multiple inputs of a transaction, where the choice of signers cannot be committed to in advance. This greatly increases the number of situations in which multi-signatures are beneficial.

2. Musig多重签名方案

2.1 Musig的相关安全假设

定义$\mathbb{G}$为a cyclic group of order $p$，其中$p$为a $k$-bit integer, and $g$ be a generator of $\mathbb{G}$。$(\mathbb{G},p,g)$称为group parameters。

security要求为：it’s infeasible to forge multi-signatures involving at least one honest signer.

2.1.1 Discrete Logarithm (DL) problem

2.1.2 Generalized Forking Lemma

2.2 Musig算法实现

包含三大类算法KeyGen，Sign和Ver。
要求setup phase结果可被checked efficiently，从而不需要依赖可信第三方来运行。

• KeyGen：每个签名者生成公私钥对$(x,X=g^x)$。
• Sign：待签名消息$m$，所有签名者公钥 L = { X 1 , ⋯ , X n } L=\{X_1,\cdots,X_n\} L={X1​,⋯,Xn​}，对于 i ∈ { 1 , ⋯ , n } i\in\{1,\cdots,n\} i∈{1,⋯,n}，签名者计算$a_i=H_{agg}(L,X_i)$，然后计算aggregated public key $\tilde{X}={\prod }_{i=1}^n{X}_i^{a_i}$；选择随机数$r_1\leftarrow {\mathbb{Z}}_q$，计算$R_1=G^{r_1},t_1=H_{com}(R_1)$，将$t_1$发送给所有其它签名者；当收齐其它签名者发来的$t_2,\cdots ,t_n$时，将$R_1$发送给所有其它签名者；当收到其它签名者发来的$R_2,\cdots ,R_n$时，验证$t_i=H_{com}(R_i))$是否成立（for all i ∈ { 2 , ⋯ , n } i\in\{2,\cdots,n\} i∈{2,⋯,n}），若不成立则停止，否则继续计算$R={\prod }_{i=1}^n{R}_i,c=H_{sig}(\tilde{X},R,m),s_1=r_1+c{a}_1{x}_1\mathrm{mod}p$，将$s_1$发送给其它所有签名者；当收到了所有的签名信息$s_2,\cdots ,s_n$时，计算$s={\sum }_{i=1}^n{s}_i\mathrm{mod}p$，最终的签名信息为$\sigma =(R,s)$。
• Ver：Given L = { X 1 , ⋯ , X n } , m , σ = ( R , s ) L=\{X_1,\cdots,X_n\},m,\sigma=(R,s) L={X1​,⋯,Xn​},m,σ=(R,s)，验签者计算$a_i=H_{agg}(L,X_i),\tilde{X}={\prod }_{i=1}^n{X}_i^{a_i}，c=H_{sig}(\tilde{X},R,m)$，验证$g^s=R{\prod }_{i=1}^n{X}_i^{a_{i}c}=R{\tilde{X}}^c$是否成立，若成立则签名验证成功。

注意Musig中的随机数$r_i$因为strong random number，不能是类似RFC6979（$f(x_i,m)$）这种确定性的值，在不同的签名过程中应使用不同的随机值，否则会存在私钥泄露的问题，详细流程如下：

2.3 Musig安全性证明

Musig中使用了3个hash函数$H_{com}$，$H_{agg}$和$H_{sig}$。

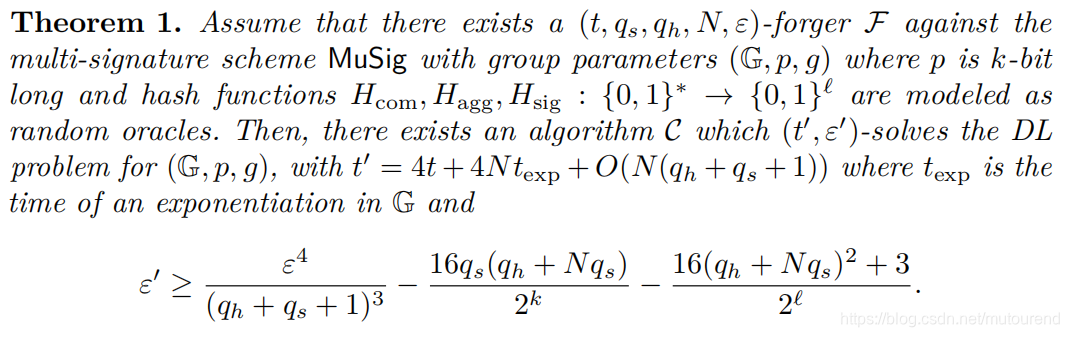
详见该论文第4章的证明。

参考资料：
[1] 博客 Key Aggregation for Schnorr Signatures
[2] A Survey of Two Signature Aggregation Techniques
[3] 2018年论文Compact Multi-Signatures for Smaller Blockchains
[4] 2018年论文BLS Multi-Signatures With Public-Key Aggregation，Full Version改名为：Compact Multi-Signatures for Smaller Blockchains