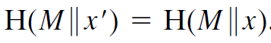Schnorr签名java实现

article/2025/10/4 4:55:46

Schnorr签名（模指数）的实现java

    • 1、算法描述
    • 2、算法的实现（java）

和ElGama数字签名一样，Schnorr数字签名方案也是基于离散对数。

Schnorr数字签名主要工作不依赖于消息，生成签名过程与消息相关的部分需要进行2n位长度的整数与n位长度的整数相乘。

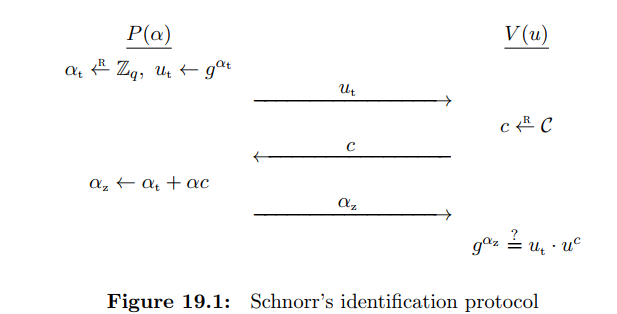
1、算法描述

算法参数分析

该方案基于素数模p，且p-1包含大素数因子q，即 p-1≡0(mod q), p一般大约取 p=2^1024, q一般大约取 q=2^160,

p是1024位整数，q是160位整数，正好等于SHA-1中Hash值的长度。

具体算法流程

第一步生成公钥和私钥对，如下：

选择素数p和q，使得q是p-1的素因子
选择整数a，使 α^q=1 mod p, 使a，p，q 构成全局公钥参数，在用户组内的每个用户都可以取此值
选择随机整数s，0<s<q ，作为用户的私钥
计算 v=a^-s mod p, 作为用户的公钥

签名

选择随机整数r，0<r<q, 并计算 x=a^r mod p, 该过程和待签名消息M无关
将x附在消息后面一起计算Hash值e， e=H(M||x)
计算 y=(r+ s*e) mod q , 签名包括(e,y)对

其他用户验证签名：

计算 x'= a^y * v^e mod p
验证是否 e=H(M||x')

对于该验证过程有：

x’≡a^y * v^e ≡a^y *a^-se ≡a^ y-se ≡ a^r ≡x mod p

所以 H(M||x’)=H(M||x)

schnorr

2、算法的实现（java）

/*** @author: mulming* @ClassName: SchnorrSignature* @date: 2020年6月16日 下午9:25:09* @Description:schnorr签名*/
public class SchnorrSignature {/*** @Author: mulming* @Description: 系统初始化阶段，把初始化的密码公共参数存放到文件中去* @param blq:选择的q的bit长度* @Date:下午9:28:20*/public static void initPara(int blq) {File  file = new File(PARAM_PATH);if(file.exists()) {System.out.println("已经存在初始化参数，为不影响已经颁发的证书，如果你强制要重新产生参数，请备份所有文件到其他路径下，并重新生产密钥对并重新签名");}else {System.out.println("系统初始化中，生产公共参数... ...");BigInteger one = new BigInteger("1");BigInteger two = new BigInteger("2");BigInteger q, qp, p, a, g;int certainty = 100;SecureRandom sr = new SecureRandom();// blq长度的q， q是p-1的素因子 //生成BigInteger伪随机数，它可能是（概率不小于1 - 1/2certainty）一个具有指定 bitLength 的素数q = new BigInteger(blq, certainty, sr);qp = BigInteger.ONE;do { // 选择一个素数 p p = q.multiply(qp).multiply(two).add(one);if(p.isProbablePrime(certainty))break;qp = qp.add(BigInteger.ONE);} while(true);while(true) {a = (two.add(new BigInteger(blq, 100, sr))).mod(p);// (2+x) mod pBigInteger ga = (p.subtract(BigInteger.ONE)).divide(q);// (p-1)/qg = a.modPow(ga, p); // a^ga mod p = 1 if(g.compareTo(BigInteger.ONE) != 0) // g!=1break;}// 存放公共参数List<String> transArryToLi = KeyPairOperate.transArryToLi(new String[] {"blq=" + blq,"q=" + q, "p=" + p, "g=" + g});KeyPairOperate.writePublicKeyToFile(PARAM_PATH, transArryToLi, false);System.out.println("...");System.out.println("初始化完成！");}}/*** @Author: mulming* @Description: 为用户生成公私钥对* @param user：传入用户的身份* @Return:void* @Date:上午9:32:18*/public static void generateKeyForUser(String user) {File  file = new File(PERFIX_PATH + user + ".properties");if(file.exists()) {System.out.println(user + "已经颁发了密钥，请备份所有文件到其他路径下，并重新签名");}else {System.out.println("密钥颁发中，请稍后");System.out.println("... ...");BigInteger sk,pk;// 私钥和公钥int blq = Integer.parseInt(KeyPairOperate.getDataFromFile(PARAM_PATH, "blq"));SecureRandom sr = new SecureRandom();// 随机数作为私钥sk = new BigInteger(blq, sr);// 私钥的话名字命名List<String> toLiSK = KeyPairOperate.transArryToLi(new String[] {"sk=" + sk});KeyPairOperate.writePublicKeyToFile(PERFIX_PATH + user + ".properties", toLiSK, false);BigInteger g = new BigInteger(KeyPairOperate.getDataFromFile(PARAM_PATH, "g"));BigInteger p = new BigInteger(KeyPairOperate.getDataFromFile(PARAM_PATH, "p"));// 公钥pk = g.modPow(sk, p);// g^w mod p  -- 注意这儿是正，所以下面验证的时候是用的负List<String> toLiPK = KeyPairOperate.transArryToLi(new String[] {user + "=" + pk});KeyPairOperate.writePublicKeyToFile(PUBLIC_KEY_PATH, toLiPK, true);System.out.println(user + " 密钥颁发完成");}}/*** @Author: mulming* @Description: 产生签名* @param sourcefilePath ： 待签名文件路径* @param user：用户身份* @Date:下午10:41:37*/public static void makeSign(String sourcefilePath, String user) {System.out.println(user+ "的文件" + KeyPairOperate.getFileName(sourcefilePath) + " 签名开始");System.out.println("... ...");BigInteger q = new BigInteger(KeyPairOperate.getDataFromFile(PARAM_PATH, "q")); // 素数 qBigInteger p = new BigInteger(KeyPairOperate.getDataFromFile(PARAM_PATH, "p")); // 素数 pBigInteger g = new BigInteger(KeyPairOperate.getDataFromFile(PARAM_PATH, "g")); // q的原根 a// 私钥BigInteger sk = new BigInteger(KeyPairOperate.getDataFromFile(PERFIX_PATH + user + ".properties", "sk")); // 私钥SecureRandom sr = new SecureRandom();BigInteger r, x, e, y; r = new BigInteger(q.bitLength(), sr); // 随机数x = g.modPow(r, p); // g^r mod p// e=H(M||x)try {MessageDigest md5 = MessageDigest.getInstance("MD5");md5.update(Files.readAllBytes(Paths.get(sourcefilePath)));md5.update(x.toString().getBytes());byte[] digest = md5.digest();// e 将BigInteger的符号大小表示法转换成一个BigInteger值e = new BigInteger(1, digest); // y s2 = ry = (r.subtract(sk.multiply(e))).mod(q);List<String> transArryToLi = KeyPairOperate.transArryToLi(new String[] {"e="+e,"y="+y});String fileName =PERFIX_PATH + user + "_sign_" + KeyPairOperate.getFileName(sourcefilePath) + ".properties";KeyPairOperate.writePublicKeyToFile(fileName, transArryToLi, false);System.out.println(user+ "的文件" + KeyPairOperate.getFileName(sourcefilePath) + "签名成功 !");} catch (Exception e1) {e1.printStackTrace();}}/*** @Author: mulming* @Description: 验证签名* @param sourcePath : 原文件路径* @param user ： 用户名* @Return:void* @Date:上午11:07:04*/public static void checkSign(String sourcefilePath, String user) {System.out.println("验证签名");BigInteger p = new BigInteger(KeyPairOperate.getDataFromFile(PARAM_PATH, "p")); // 素数 pBigInteger g = new BigInteger(KeyPairOperate.getDataFromFile(PARAM_PATH, "g")); // q的原根 aBigInteger pk = new BigInteger(KeyPairOperate.getDataFromFile(PUBLIC_KEY_PATH, user));//  公钥String fileName =PERFIX_PATH + user + "_sign_" + KeyPairOperate.getFileName(sourcefilePath) + ".properties"; BigInteger e = new BigInteger(KeyPairOperate.getDataFromFile(fileName, "e")); // e 签名信息1： 产生的签名信息BigInteger y = new BigInteger(KeyPairOperate.getDataFromFile(fileName, "y"));; // y 签名信息2: 加密后的消息// 计算的 x'BigInteger x1 = g.modPow(y, p); // g^y mod p -- yBigInteger x2 = (pk.modPow(e, p)).mod(p); // pk^e mod p BigInteger x = x1.multiply(x2).mod(p); // x1*x2 mod p = (g^y)*(pk^e)mod ptry {MessageDigest md5 = MessageDigest.getInstance("MD5");md5.update(Files.readAllBytes(Paths.get(sourcefilePath)));md5.update(x.toString().getBytes());byte[] digest = md5.digest();BigInteger h = new BigInteger(1, digest);System.out.println("... ...");if(e.equals(h))System.out.println(user+ "的文件" + KeyPairOperate.getFileName(sourcefilePath) + "验证通过 !");elseSystem.out.println(user+ "的文件" + KeyPairOperate.getFileName(sourcefilePath) + "验证失败 !");} catch (Exception e1) {e1.printStackTrace();}}
}

** 注：如果需要完整一点的代码，可以在下面留下邮箱，我发送。**


http://chatgpt.dhexx.cn/article/Aux0wXcI.shtml

相关文章

Blind Schnorr Signature

Blind Schnorr Signature

1. 引言 前序博客有&#xff1a; 盲签名 blind signature Blind Schnorr Signature交互签名Demo见&#xff1a; Blind Schnorr Signature Interactive Demo 参考资料 [1] Schnorr Applications: Blind Signatures
阅读更多...
本体技术视点 | 为什么 BIP - 340 选择引入 Schnorr 签名算法？

本体技术视点 | 为什么 BIP - 340 选择引入 Schnorr 签名算法？

引言 备受瞩目的技术升级 Taproot 软分叉将于最近激活&#xff0c;激活高度为 709632&#xff0c;距今已不足 500 个区块。此次升级包括三个改进提案&#xff0c;分别是 BIP - 340、BIP - 341 和 BIP - 342。其中&#xff0c;BIP - 340 引入了 Schnorr 签名&#xff0c;BIP - …
阅读更多...
【密码学】Schnorr认证，Schnorr签名，安全性证明

【密码学】Schnorr认证，Schnorr签名，安全性证明

Schnorr是Sigma协议的实例&#xff0c;从Schnorr 认证协议和Schnor签名两个部分来介绍。在前面关于认证协议的讲述中&#xff0c;用到了一些特定的符号&#xff0c;这里会继续使用。 首先认识Schnorr认证协议&#xff0c;定义如图所示 Schnorr认证协议和Schnorr签名方案的安全…
阅读更多...
零知识证明系列之二——Schnorr协议

零知识证明系列之二——Schnorr协议

​Schnorr协议简介 Schnorr协议是由德国数学家和密码学家Claus-Peter Schnorr在1991年提出&#xff0c;是一种基于离散对数难题的知识证明机制。Schnorr本质上是一种零知识的技术&#xff0c;即Prover声称知道一个密钥x的值&#xff0c;通过使用Schnorr加密技术&#xff0c;可…
阅读更多...
Schnorr 签名方案和 BLS 签名方案的全面对比

Schnorr 签名方案和 BLS 签名方案的全面对比

原文&#xff1a;https://medium.com/cryptoadvance/bls-signatures-better-than-schnorr-5a7fe30ea716https://medium.com/cryptoadvance/how-schnorr-signatures-may-improve-bitcoin-91655bcb4744 Schnorr 签名算法最初是由德国密码学家 Claus Schnorr 于 2008 年提出的&…
阅读更多...
Schnorr签名算法(初始化和签名)C语言实现

Schnorr签名算法(初始化和签名)C语言实现

Schnorr签名算法(初始化和签名) Schnorr签名算法(验证) Schnorr签名算法(正确性) Schnorr签名算法(举例) Schnorr签名算法(举例) C语言实例 #include <stdlib.h> #include <stdio.h> #include <time.h> int xy[22]; // 判断两个数是否互质 int isHuZhi(int …
阅读更多...
Schnorr数字签名方案

Schnorr数字签名方案

Schnorr数字签名方案 Schnorr签名算法最初由德国密码学家claus schnorr于2008年提出&#xff0c;在密码学中&#xff0c;它是一种数字签名方案&#xff0c;以其简单著称 Schnorr数字签名方案也是基于离散对数的&#xff08;基于离散对数的还有ElGamal数字签名方案、DSA数字签…
阅读更多...
记录我看的密码学方案中的技术，Shamir秘密共享，Schnorr零知识证明，EIGamal密码体制

记录我看的密码学方案中的技术，Shamir秘密共享，Schnorr零知识证明，EIGamal密码体制

记录我看的论文中基于的技术&#xff0c;对他们进行大概介绍 Shamir 秘密共享方案零知识证明EIGamal密码体制 Shamir 秘密共享方案 1979年&#xff0c;Shamir提出的一个基于拉格朗日插值的(k,n)门限方案 目的&#xff1a;可以将秘密s分给n个成员&#xff0c;规定至少有k&#…
阅读更多...
schnorr签名和batch verification

schnorr签名和batch verification

schnorr 签名 概念&#xff1a;Schnorr签名算法最初是由德国密码学家ClausSchnorr于2008年提出的&#xff0c;在密码学中&#xff0c;它是一种数字签名方案&#xff0c;以其简单高效著称 原理&#xff1a;其安全性基于某些离散对数问题的难处理性。 签名过程&#xff1a; 和…
阅读更多...
密码学学习笔记(十六 )：Schnorr签名算法

密码学学习笔记(十六 )：Schnorr签名算法

交互式零知识证明 零知识证明(ZKP)就是不会将证据泄露给验证者的知识证明。Schnorr身份认证识别协议是一个交互式ZKP&#xff0c;它满足了完备性、可靠性、零知识性。所谓的交互式ZKP方案通常包含3个步骤&#xff08;承诺、挑战和证明&#xff09;&#xff0c;在文献中通常被称…
阅读更多...
ECDSA VS Schnorr signature VS BLS signature

ECDSA VS Schnorr signature VS BLS signature

1. ECDSA ECDSA&#xff0c;全称为Elliptic curve Digital Signature Algorithm&#xff0c;采用Elliptic curve cryptography来实现的数字签名算法。 公私钥对 ( p k , P ) (pk,P) (pk,P)&#xff0c;其中公钥 P p k G Ppk\times G PpkG&#xff0c; G G G为所选椭圆曲线的…
阅读更多...
BSV 上的 Schnorr 签名

BSV 上的 Schnorr 签名

我们已经在 BSV 上实现了 Schnorr 签名。这是第一个也是唯一一个已知的实现&#xff0c;没有对原始协议进行任何更改。 一笔交易一个签名 Schnorr 是一种可以用于替代比特币签名当前使用的 ECDSA 算法的替代算法。一个关键优势是&#xff0c;同一交易的一个输入或多个输入中的多…
阅读更多...
深入浅出零知识证明（一）：Schnorr协议

深入浅出零知识证明（一）：Schnorr协议

最近在学习零知识证明&#xff0c;因为内容很多并且难度也大&#xff0c;想根据自己的学习路线做一系列总结&#xff0c;这是第一篇文章&#xff0c;主要介绍零知识证明的一些重要概念和思想&#xff0c;可以对零知识证明有直观的理解&#xff0c;然后讲解一个经典简洁的零知识…
阅读更多...
密码学——Schnorr签名算法

密码学——Schnorr签名算法

一、基本知识 1.1 概述 Schnorr签名算法最初是由德国密码学家ClausSchnorr于2008年提出的&#xff0c;在密码学中&#xff0c;它是一种数字签名方案&#xff0c;以其简单高效著称&#xff0c;其安全性基于某些离散对数问题的难处理性。 1.2 椭圆曲线上的计算 密码学中&…
阅读更多...
什么是 Schnorr 签名？

什么是 Schnorr 签名？

在密码学中&#xff0c;Schnorr 签名是由 Schnorr 签名算法生成的数字签名。 与大多数区块链不同&#xff0c;BTC自其早期以来基本保持不变&#xff0c;大多数升级都是有限的&#xff0c;并旨在增强网络的效率而不是功能。BTC协议的更新是非常罕见的&#xff0c;并且通常用于技…
阅读更多...
史上最全的Schnorr签名方案和BLS签名方案的全面对比

史上最全的Schnorr签名方案和BLS签名方案的全面对比

前言 Schnorr 签名算法最初是由德国密码学家 Claus Schnorr 于 2008 年提出的&#xff0c;而来自区块链协议公司 Blockstream 的密码学家 Gregory Maxwell、Pieter Wuille 等人&#xff0c;则在 2018 年提出了一种名为 MuSig 的 Schnorr 签名方案&#xff0c;这也是我们即将探索…
阅读更多...
Schnorr身份识别方案

Schnorr身份识别方案

Schnorr身份识别协议是又一个零知识证明协议&#xff0c;相比Fiamt协议有两点不同&#xff0c;一是其安全性依赖于离散对数的困难性&#xff0c;二是该方案使用乘法群&#xff0c;从而可以提前计算了一些参数&#xff0c;减小了证明者实时计算开销&#xff0c;特别适合计算能力…
阅读更多...
Schnorr协议：非交互零知识身份证明和数字签名

Schnorr协议：非交互零知识身份证明和数字签名

本文首发公众号区块链之美&#xff01;致力于区块链技术研究&#xff0c;传播区块链技术和解决方案、区块链应用落地、区块链行业动态等。 摘要&#xff1a;本篇文章介绍Schnorr的两大应用场景&#xff1a;从交互式零知识身份证明到非交互零知识身份证明、数字签名实现基本原理…
阅读更多...
matlab实现rrt算法

matlab实现rrt算法

这一部分算法强烈推荐两篇博客&#xff0c;尤其是第一篇博客介绍算法的原理非常简单易懂&#xff1a; https://blog.csdn.net/weixin_43465857/article/details/96451631 https://www.cnblogs.com/long5683/p/11795987.html https://blog.csdn.net/aoyousihaiqiuqihuang/articl…
阅读更多...
RRT*算法的原理简介以及Python实现代码

RRT*算法的原理简介以及Python实现代码

![RRT算法原理图](https://img-blog.csdnimg.cn/20210420101155956.png?x-oss-p RRT大致流程 1.初始化随机树tree&#xff0c;以空的随机树开始添加节点&#xff0c;最开始只有Qinit。 2.执行sample函数&#xff0c;在地图中获得一个随机点Qrand。 3.遍历tree中所有节点&#…
阅读更多...
推荐文章

Copyright @ 2022~2023