文章目录
- 前言
- 递归的概念
- 递归的两个必要条件
- 例题
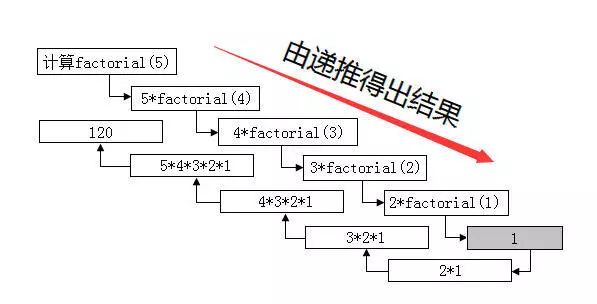
- 1.递归实现阶乘
- 2.递归实现strlen函数
- 3.计算一个正整数各位数字的和
- 4.递归实现整数n的整数k次方
- 5.递归实现斐波那契数
- 6.递归实现字符串逆序
- 7.汉诺塔
- 8.青蛙跳台阶
- 9.将一个十进制数以二进制的形式打印
前言
本文总结了几个递归基础例题,c语言实现
递归的概念
C语言允许函数调用它自己,这种调用过程叫做递归(recursion)
递归的两个必要条件
- 存在限制条件,当满足这个限制条件的时候,递归便不再继续
- 每次递归调用之后越来越接近这个限制条件
例题
1.递归实现阶乘
#include<stdio.h>
int Fac(int n)
{if(n<=1)return 1;elsereturn n*Fac(n-1);
}int main()
{int n;scanf("%d",&n);int ret=Fac(n);printf("%d\n",ret);return 0;
}
2.递归实现strlen函数
#include<stdio.h>
int Strlen(const char* str)
{if('\0'==*str)return 0;elsereturn 1+Strlen(str+1);
}int main()
{char arr[20]="Hello world!";int ret=Strlen(arr);printf("%d\n",ret);return 0;
}
3.计算一个正整数各位数字的和
#include<stdio.h>
unsigned fun(unsigned n)
{if(n>9)return n%10+fun(n/10);elsereturn n;
}int main()
{unsigned a=0;scanf("%d",&a);printf("%d\n",fun(a));return 0;
}
4.递归实现整数n的整数k次方
#include<stdio.h>
int fun(int n,int k)
{if(0==k)return 1;elsereturn fun(n,k-1);
}int main()
{int n;int k;scanf("%d %d",&n,&k);printf("%d\n",fun(n,k));return 0;
}
5.递归实现斐波那契数
#include<stdio.h>
int Fib(int n)
{if(n<=2)return 1;elsereturn Fib(n-1)+Fib(n-2);
}int main()
{int n;scanf("%d",&n);printf("%d\n",Fib(n));return 0;
}
6.递归实现字符串逆序
#include<stdio.h>
#include<string.h>
void reverse_string(char* str)
{int len=strlen(str);char tmp=*str;*str=*(str+len-1);*(str+len-1)='\0';if(strlen(str+1)>=2)reverse_string(str+1);*(str+len-1)=tmp;
}int main()
{char arr[20]="hello world!";printf("%s\n",arr);reverse_string(arr);printf("%s\n",arr);return 0;
}

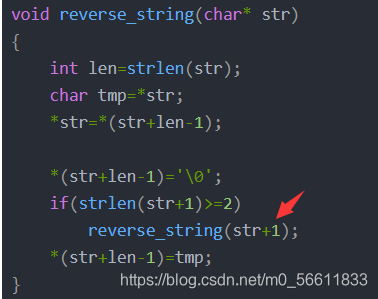
注意,前面6次函数调用都没有执行完该次调用,只执行到了上图箭头所指处,而在第6次调用时,if条件不满足,执行语句
*(str+len-1)=tmp;
每一级调用执行完该语句便返回上一级调用,字符数组里的内容依次变为

原字符串最后一个’\0’始终没有动到
7.汉诺塔
问题描述:
三根柱子A,B,C,最初一摞盘子下大上小的放在A柱子上,现要将盘子移动到C柱子上,要求:
- 一次只能移动一个盘子
- 大盘子不能放在小盘子上
请给出一个可行的方案(每一步怎么移动)
#include<stdio.h>
int count = 1;
void hanoi(int n, char a, char b, char c)//n个盘子从a借助b到c
{if (0 == n)return;hanoi(n - 1, a, c, b);printf("step %d: move %d from %c to %c\n", count++, n, a, c);hanoi(n - 1, b, a, c);//n-1个盘子从b借助a到c
}int main()
{int n;while (scanf("%d", &n)){hanoi(n, 'A', 'B', 'C');}return 0;
}
思路
为方便描述,盘子由小到大依次叫做1,2……,n
下面先用N=3的情形下给出一个解法,以得到一个直观的印象
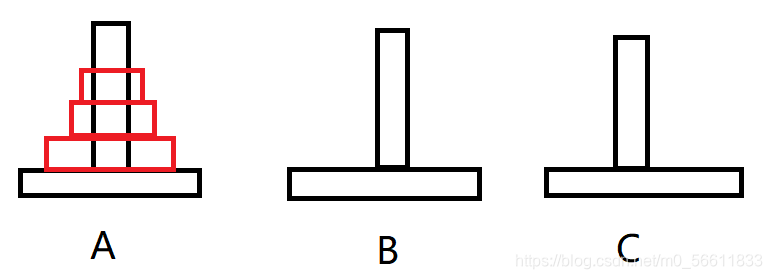
第一步:
先把1移到C
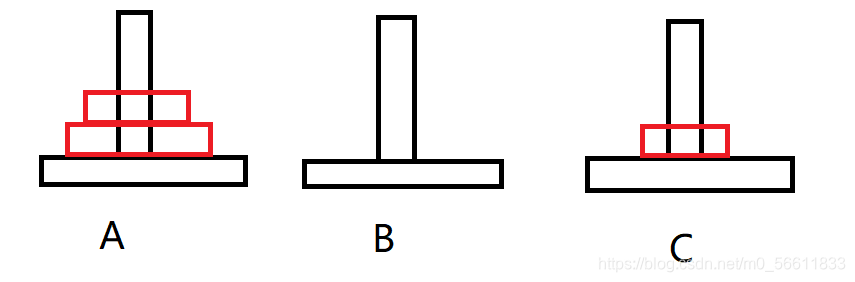
第二步:
再把2移到B
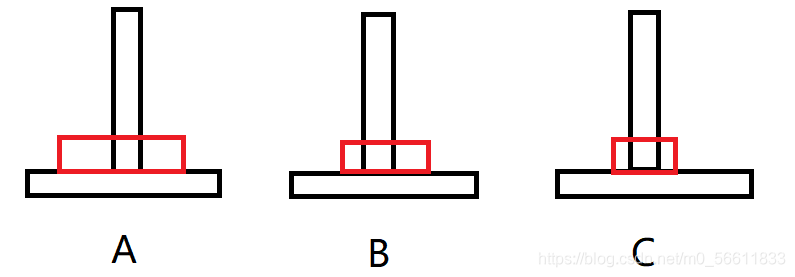
第三步:
把1移回B
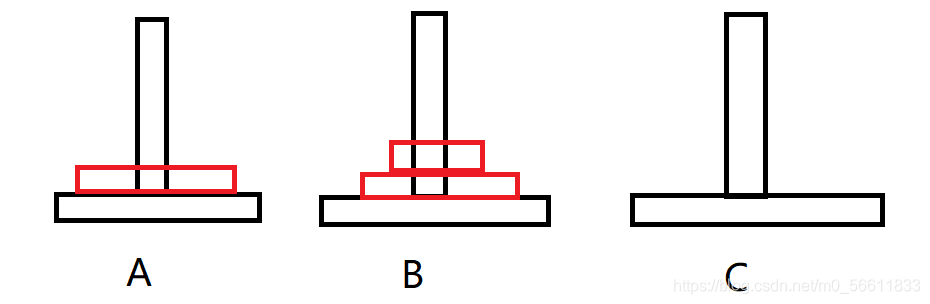
第四步:
把3移到C
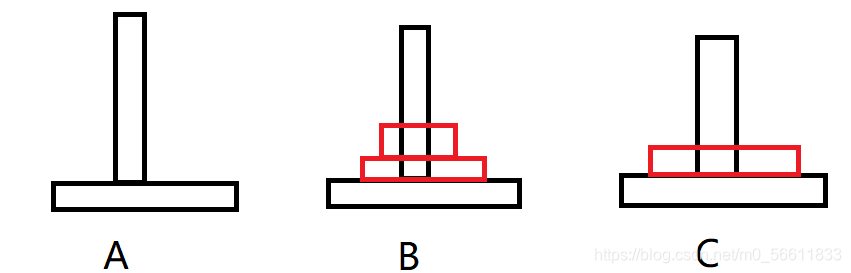
第五步:
把1移到A
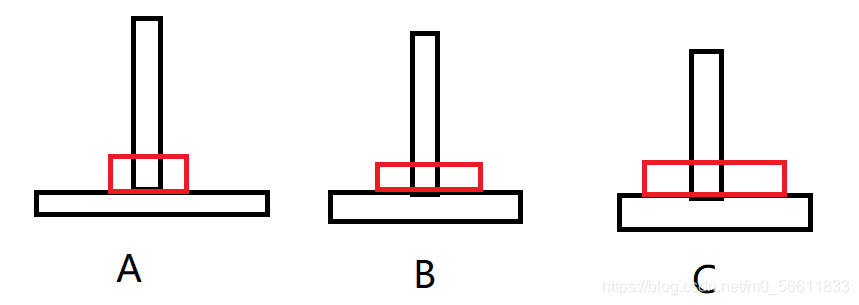
第六步:
把2移到C
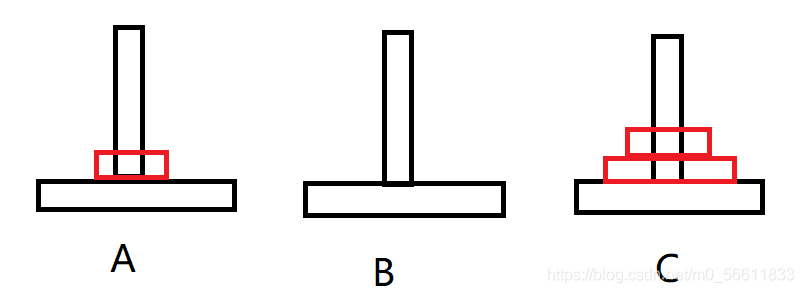
第七步:
把1移到C,就完成了
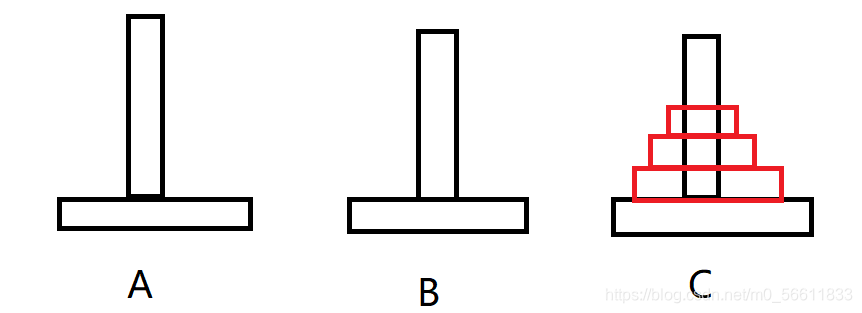
以上的做法其实是遵循以下规则移动的:
对于有n个盘子
- 将n-1个盘子由A(借助C)移动到B
- 将第n个盘子由A移动到C
- 将n-1个盘子由B(借助A)移动到C
以上三步便是汉诺塔问题的迭代公式,接下来只要考虑如何实现第一和第三步即可
那么如何将n-1个盘子由A(借助C)移动到B呢?
- 将n-2个盘子由A(借助B)移动到C
- 将第n-1个盘子由A移到B
- 将n-2个盘子由C(借助A)移动到B
那么如何将n-1个盘子由B(借助A)移动到C呢?
- 将n-2个盘子由B(借助C)移动到A
- 将第n-1个盘子由B移到C
- 将n-2个盘子由A(借助B)移到C
8.青蛙跳台阶
问题描述:
一只青蛙一次可以跳一级台阶或跳两级台阶(不能往回跳),问要跳上n级台阶有几种跳法
#include<stdio.h>int frog(int n)
{if (n == 1){return 1;}if (n == 2){return 2;}return frog(n - 1) + frog(n - 2);
}
int main()
{int n;scanf("%d", &n);int ways = frog(n);printf("%d\n", ways);return 0;
}
思路:
当N=1时,一种方法;
当N=2时,一次跳两级或两次跳一级,两种方法;
当N=3时,若先跳一级,则接下来的方法数即n=2时的方法数;若先跳两级,则接下来的方法数为n=1的方法数,根据加法原理,n=3的方法数为n=2的方法数+n=1的方法数
以此类推,N=n时的方法数为N=n-1的方法数加上N=n-2的方法数
本质上,这是和斐波那契数相同的问题
9.将一个十进制数以二进制的形式打印
void to_binary(int n);int main()
{int number;scanf("%d", &number);to_binary(number);return 0;
}void to_binary(int n)
{if (n >= 2)to_binary(n / 2);printf("%d", n%2);return;
}从本题可以看出,递归在处理倒序问题时非常方便。
对于一个十进制数字,对2求模得到的结果实际上是待输出二进制数的最后一位,这一规律提示我们在递归函数的调用之前计算n%2,在递归调用之后打印计算结果。这样计算的第一个值正好是最后一个打印的值。