（旋转体体积的计算）利用元素法简单解答空间几何体问题——高等数学

article/2025/10/25 16:37:00

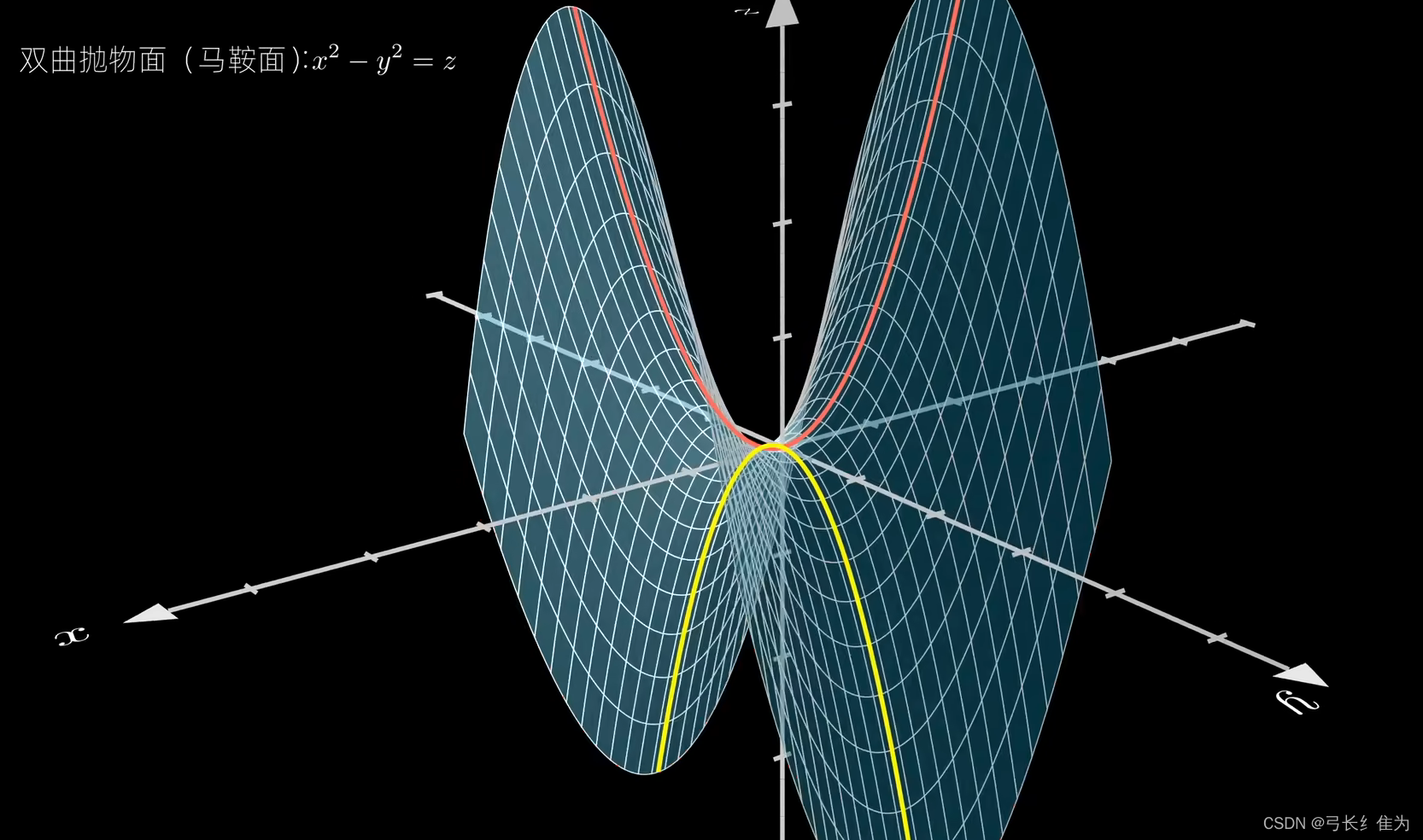
相信很多人初学的时候和我一样对这种三维空间的几何体计算方面有困难。我也曾百度过关于几何体体积/表面积的求法，但是始终不是很明白百度上的那种方法。这篇文章让你彻底理解这个万能的几何思想：“元素法”

结合配图和图旁解释说明学习，请细品

首先告诉大家：dx，dy，dz，ds，不管d什么，都是极小的微分元素，可以说取极限趋近于0

注意：下面所有图里面画的蓝线都是我取的一个极小的几乎没有宽度的元素条！

文章目录

  • 元素法的思想（三步走）
  • 一、求平面图形的面积
  • 二、求旋转体的体积
    • 2.1 绕x轴旋转
    • 2.2 绕y轴旋转
    • 2.3 绕z轴旋转
    • 2.4 截口面积已知的几何体体积
  • 三、弧长
  • 四、空间曲面的面积(表面积)
  • 五、古尔丁定理
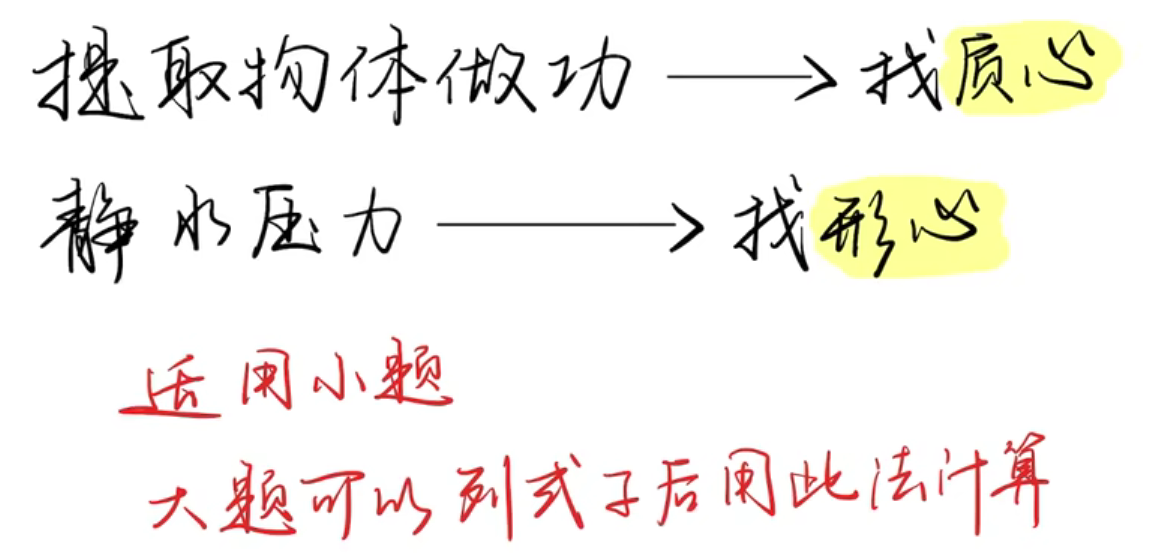
  • 六、定积分物理应用

元素法的思想（三步走）

在这里插入图片描述
具体思路如图所示
在这里插入图片描述
求体积和表面积的方法同理（下面会详细说明）。所谓实践得结论，接下来就为大家举举例子

一、求平面图形的面积

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

二、求旋转体的体积

2.1 绕x轴旋转

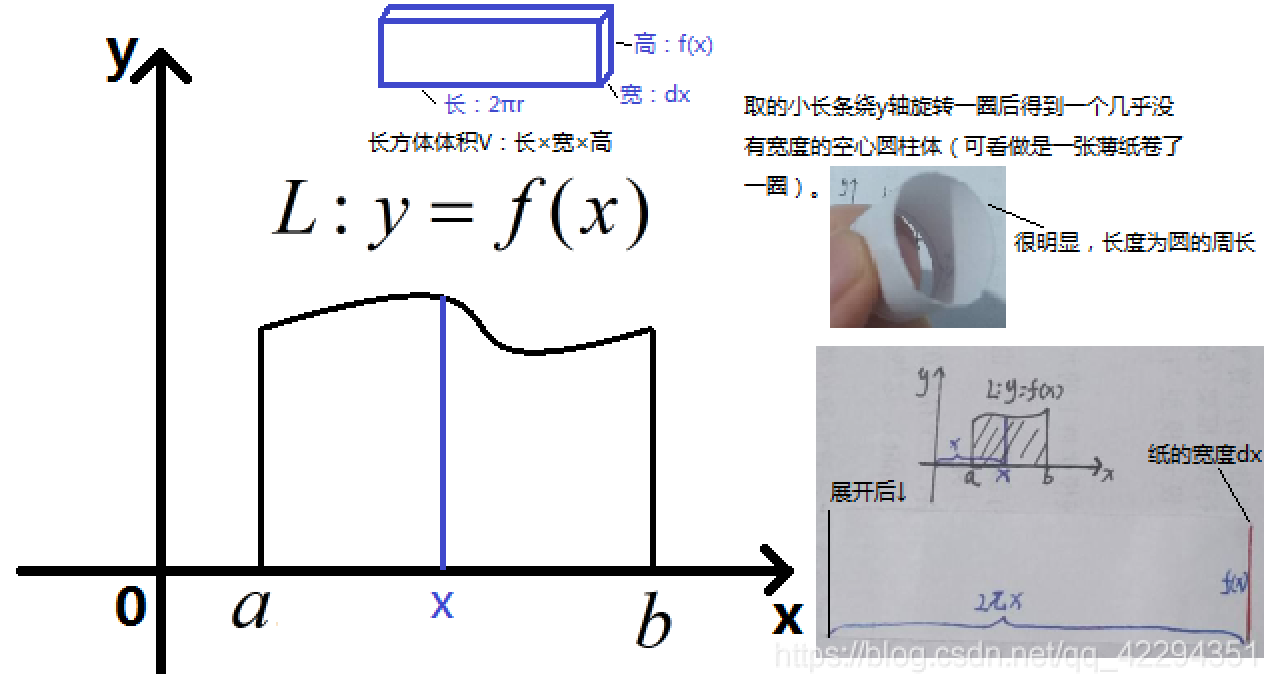
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2.2 绕y轴旋转

这也是我们常常听到的柱壳法公式的由来。看我卷的那张纸，像不像一个柱子外面的壳？

在这里插入图片描述

在这里插入图片描述

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2.3 绕z轴旋转

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

2.4 截口面积已知的几何体体积

如图所示，切面是一个几乎没有高度的圆柱体
在这里插入图片描述
几何体体积的切片法是同样的思想，只不过是取的一层一层的体积叠起来。类似于上图这种切法，只不过上图是把面积一片一片叠起来。
这样说来，感觉二重积分取投影的方法也类似哈，就看自己怎么理解了。

三、弧长

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
(下面这道题属于第一类曲线积分(对弧长的曲线积分)的计算，因为思想和2)是一样的，所以我先提一下)
在这里插入图片描述

四、空间曲面的面积(表面积)

ds即弧长，因为求的表面积，所以很多小段的弧长堆起来就成了外表层了
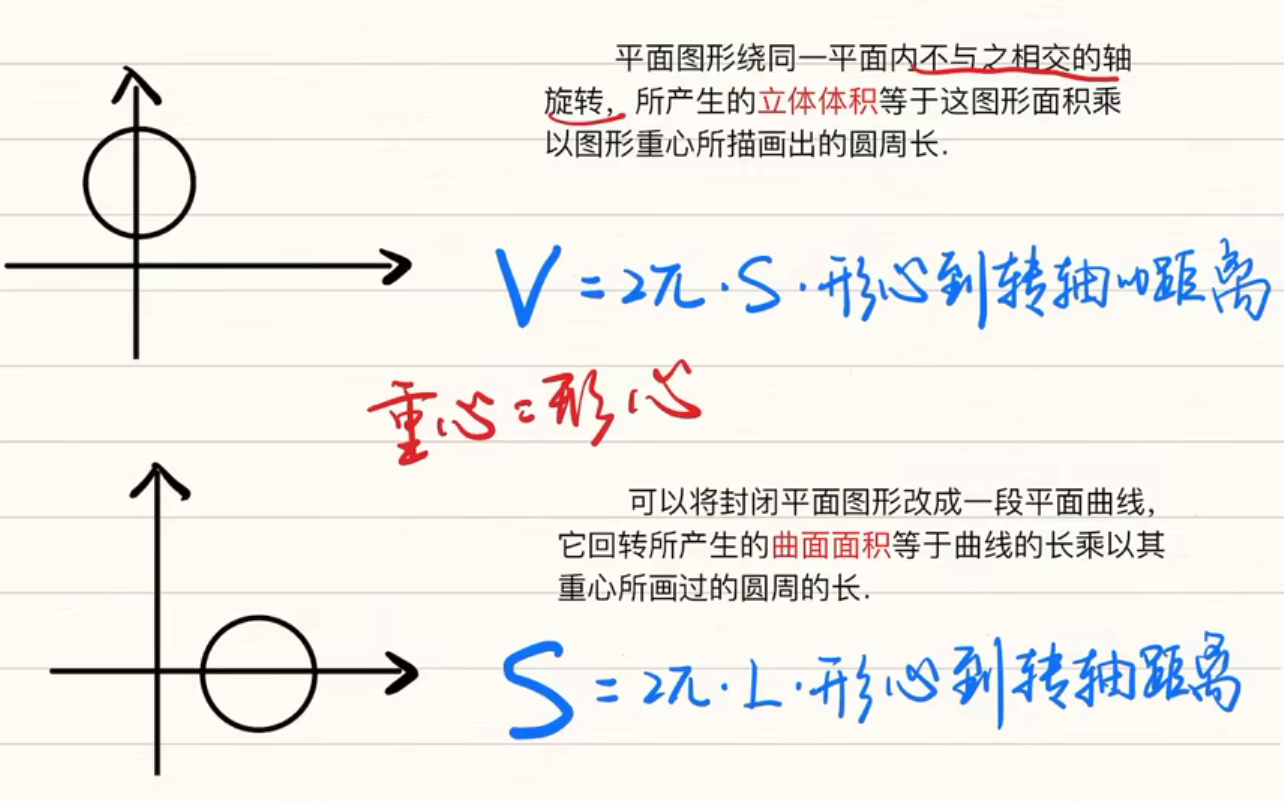
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
在这里插入图片描述

五、古尔丁定理

［考研数学］古尔丁定理 一类旋转体体积及表面积问题


在这里插入图片描述

六、定积分物理应用

［考研数学］定积分物理应用 秒杀！！ 4道例题讲解


在这里插入图片描述


http://chatgpt.dhexx.cn/article/X4W9Rg10.shtml

相关文章

【5】Git删除本地分支和远程分支

【5】Git删除本地分支和远程分支

【5】Git删除本地分支和远程分支 1.删除本地分支 不能删除当前所在分支，需要切换到其他分支才能删除分支。 删除分支命令 git branch -d 分支名称2.删除远程分支两步搞定 2.1.删除远程分支命令 git branch -r -d origin/将要删除的分支名称 此刻提示远程分支已经…
阅读更多...
git删除本地分支在远程仓库已不存在的分支

git删除本地分支在远程仓库已不存在的分支

查看本地及远程所有分支 git branch -a 查看origin的详细信息 git remote show origin 同步origin主机对于git分支的删除操作，即去除Git Graph无用远程分支节点 git remote prune origin 在本地删除远程不存在的分支（-d：删除，如…
阅读更多...
Git系列之Git删除本地分支和远程分支

Git系列之Git删除本地分支和远程分支

文章の目录 1、切换到不删除的分支，这里以master分支为例2、查看已有的本地和远程分支3、删除远程分支dev4、删除后，再次查看分支情况5、删除本地分支dev6、删除后，再次查看分支情况写在最后 1、切换到不删除的分支，这里以master分…
阅读更多...
使用sourcetree 删除本地分支和远程分支

使用sourcetree 删除本地分支和远程分支

1.本地分支删除 右键目标分支，删除即可。 注意：这里的删除是本地删除，不影响远程仓库。另外，当你切换到目标分支时，不能进行删除操作。 2.远程分支删除 右键目标分支，删除即可。这里是删除远程分支。慎重
阅读更多...
git 命令怎么删除本地分支

git 命令怎么删除本地分支

查看所有分支 查看项目的分支： 包括本地和远程 git branch -a删除本地分支 git branch -d git branch -d 分支名-d 是 --delete 的缩写,在使用 --delete 删除分支时，该分支必须完全和它的上游分支 merge 完成。 如果没有完成 merge 就会报下面的 gi…
阅读更多...
TortoiseGit删除本地分支和远程分支

TortoiseGit删除本地分支和远程分支

一、删除本地分支： 1、我们想删除dev_1分支前，我们需要将本地代码库切换到其它分支，比如：dev_2,切换方法如下： 右键------switch/checkout： 其中，带有remotes的是远程分支，我们要选…
阅读更多...
Git 中删除本地分支和删除远程分支是两回事儿

Git 中删除本地分支和删除远程分支是两回事儿

目录 本地操作 1. 创建本地分支 2. 删除本地分支 远端操作 1. 创建远程分支 2. 删除远程分支 本地操作 1. 创建本地分支 在本地仓库中创建本地分支，Git 命令如下： git branch h265 在本地仓库中删除本地分支，Git 命令如下&#xff1a…
阅读更多...
git 删除本地分支/远程分支

git 删除本地分支/远程分支

Git 删除本地分支指令： # 语法 git branch -d 本地分支名称# 实例 $ git branch -d zzg-mastrGit 删除远程分支指令: # 语法 git push origin --delete 远程分支名称# 实例 git push origin --delete mainGit Bash 控制台： zzgLAPTOP-8R0KHL88 MINGW6…
阅读更多...
帅某---考研---空间直线绕坐标轴旋转、二次曲面方程

帅某---考研---空间直线绕坐标轴旋转、二次曲面方程

一.空间直线绕坐标轴旋转 注：1.本说明以Z轴为例子，其他轴类同； 2.直线绕直线旋转对应的为二次曲面方程，属于超纲内容。考察内容为：给定二次曲面方程，只需要知道其曲面类型。 二.二次曲面方程 1.介绍及其…
阅读更多...
线性代数学习笔记——第九十讲——化二次曲面为标准方程

线性代数学习笔记——第九十讲——化二次曲面为标准方程

1. 用正交变换化二次型为标准型的方法 2. 化二次曲面为标准方程示例1 3. 化二次曲面为标准方程的一般方法 4. 化二次曲面为标准方程的示例2 5. 化二次曲面为标准方程的示例3
阅读更多...
曲面研究的两个基本问题、旋转曲面、柱面、二次曲面

曲面研究的两个基本问题、旋转曲面、柱面、二次曲面

曲面及其方程 曲面方程概念 F（x,y,z）0就是曲面的方程 例如球面方程可以表示为 旋转曲面 母线：平面曲面 轴： 例如 绕哪一个轴旋转，哪一个轴就不变，另外一个量变成正负根号下平方和 总结规律 柱面 …
阅读更多...
解析几何 曲线与二次曲面 曲面方程与坐标变换(2.1,2.2)

解析几何 曲线与二次曲面 曲面方程与坐标变换(2.1,2.2)

一.曲面的方程(2.1) 1.柱面: 2.锥面: 3.旋转面: 二.坐标变换(2.2) 1.平面坐标轴旋转: 2.空间坐标轴变换: 3.欧拉角(Euler Angles):
阅读更多...
利用正交变换判断二次曲面类型

利用正交变换判断二次曲面类型

利用正交变换判断二次曲面类型 正交变换是欧式空间保持向量内积不变的线性变换。不仅保持向量的长度不变，而且还保持向量 的夹角不变。二维或三维空间中的旋转变换、关于某一条直线或平面的对称变换都是正交变换．投影变换、平移变换不是正交变换&#xf…
阅读更多...
TikZ作图：九种二次曲面（附代码）

TikZ作图：九种二次曲面（附代码）

如何用TikZ/pgfplots宏包绘制《解析几何》中的二次曲面图像？ 本文将逐一给出示例代码。 导言区设置如下： \documentclass[border{1.2cm 0.1cm 1.2cm 0.1cm}]{standalone} \usepackage{pgfplots} \usepgfplotslibrary{patchplots} \usepgfplotslibrary…
阅读更多...
二次曲面的绘制

二次曲面的绘制

#include "stdafx.h" #include <GL/glut.h> #include <math.h> /*声明四个二次曲面物体*/ GLUquadricObj *quadObj1; GLUquadricObj *quadObj2; GLUquadricObj *quadObj3; GLUquadricObj *quadObj4; GLUquadricObj *quadObj5; stat…
阅读更多...
【高等数学】二次曲面直观几何形态展示

【高等数学】二次曲面直观几何形态展示

一、圆柱面 二、椭圆柱面 三、 双曲柱面 四、抛物柱面 五、圆锥面 六、椭圆锥面 七、球面 八、椭球面 九、椭圆抛物面 十、单叶双曲面 十一、双叶双曲面 十二、双曲抛物面&#xff08;马鞍面&#xff09;
阅读更多...
数分下第5讲（8.3节） 二次曲面方程和曲线方程

数分下第5讲（8.3节） 二次曲面方程和曲线方程

第3.1讲 二次曲面方程和曲线方程 本讲是空间解析几何中的曲面和曲线方程&#xff0c;要求掌握二次曲面的生成方法和画图。 文章目录 第3.1讲 二次曲面方程和曲线方程学习要点一、二次曲面方程1、球面方程2、柱面方程&#xff1a;缺少一个变量3、旋转曲面&#xff08;旋转&…
阅读更多...
【学习记录】二次曲线、二次曲面、对偶二次曲线、对偶二次曲面

【学习记录】二次曲线、二次曲面、对偶二次曲线、对偶二次曲面

一、二次曲线与对偶二次曲线 最近在看基于椭球体的物体SLAM过程中&#xff0c;经常涉及到椭球体的空间几何知识&#xff0c;这里先补充一下一些空间几何相关的基础&#xff0c;参考链接。 椭球体本身属于二次曲面的一种&#xff0c;二次曲面是对空间形状的描述&#xff0c;属于…
阅读更多...
空间二次曲面数据拟合算法推导及仿真分析

空间二次曲面数据拟合算法推导及仿真分析

在上一篇的博客球面数据拟合算法简介中&#xff0c;笔者详细介绍了关于空间球面数据拟合的算法公式推导并给出了相应的Matlab代码及其仿真分析。本次笔者将上面这一情况进行更一般的推广&#xff0c;即取消了球面数据这一限制&#xff0c;数据可以是椭球面形式的&#xff0c;也…
阅读更多...
通过Python绘制九种二次曲面

通过Python绘制九种二次曲面

二次曲面 python中绘制三维图需要将坐标系声明为3d。 球面方程为 x 2 y 2 z 2 R 2 x^2y^2z^2R^2 x2y2z2R2 写为极坐标形式为 x R sin ⁡ θ cos ⁡ φ y R sin ⁡ θ sin ⁡ φ z R cos ⁡ θ \begin{aligned} x&R\sin\theta\cos\varphi\\ y&R\sin\theta\sin\…
阅读更多...
推荐文章

Copyright @ 2022~2023