上午课程
课程大纲
1.web
重点介绍了web1.0和web2.0时代采用的技术,web1.0时代主要采用dos攻击html静态网页,虽然静态网页没有数据库,但是拒接服务式攻击可以将网络响应攻击瘫痪,web2.0时代新增了数据库,黑客所攻击的目标不再是服务器,而是数据库,对现在的网络攻击有了一个更加全面的认识。
web1.0和web2.0

数据库和服务器可以放在一起,数据库可以单独出来。
搭建一个网站,需要有数据库,中间件(tomcat、Apache),语言解析器,前端语言解析器在浏览器上,每一个中间件都是一个服务,计算机上每一个服务都有一个端口,以IIS和Apcahe为例端口都是80,ssh端口是22。
客户端和服务器之间通过IP地址建立连接。
网页请求的流程
1)打开浏览器,地址栏输入网址
2)DNS解析,获取IP地址;
本机系统先访问本机的主机文件和缓存,再去找dns(叫做本地dns)询问,一般在运营商那里。
3)建立TCP连接,3次握手;
客户端首先与服务器建立连接,发送SYN请求;服务器收到请求后,发送SYN / ACK确认连接请求;客户端收到后再发送ACK进行确认。
tcp三次握手流程
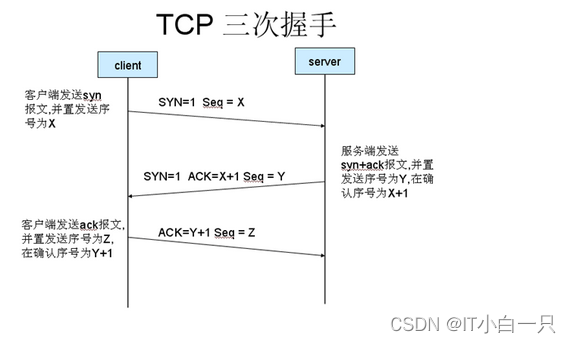
4)发送HTTP请求报文;
向web服务器发送请求,告诉服务器需要查找使用的资源
5)服务器接收请求并作处理;
服务器接受到请求后,查找客户端想使用的资源
6)服务器发送HTTP响应报文;
7)断开TCP连接,4次握手。
http无状态协议的特点
2.HTTP
B:http协议
HTTP是Hyper Text Transfer Protocol(超文本传输协议)的缩写。HTTP协议是用于从WWW服务器传输超文本到本地浏览器的传送协议。
HTTP是一个应用层协议,由请求和响应构成,是一个标准的客户端服务器模型。HTTP是一个无状态的协议。
数据请求分为两种POST和GET
GET请求的所提交的所有数据都在URL中体现,不利于提交复杂的数据,且安全性相对较低,而POST请求可以将主要数据放在请求正文中提交,常用于提交复杂数据(如图像、文件等)或敏感信息(如用户鉴权信息)
user-Agent:浏览器内核
accept:文件类型
accebt-lunagee:物理地址
en-gb英国
accept-Hncoding:加密文件,压缩的方式
Connect-Type:请求的数据类型
Origin:请求来源
Connection:是否建立链接
Referere:网页从哪里跳转到哪里
C:URL
url处理流程
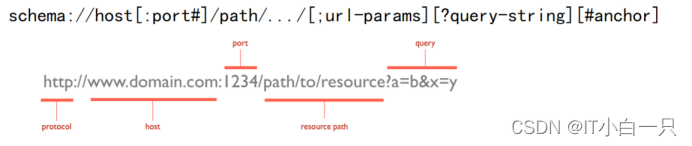
网站处理之后解析完成之后响应,将源码放入响应正文中,生成响应报文,解析源码后放入到网页中
http//1.1 302 Found响应状态,302是状态码,作用是重定向(网页从一个网页跳转到另一个网页就会发生重定向)
404以4开头的就是客户端错误,更多如下图
各种响应状态所代表的作用

3. web安全
服务器处理过程
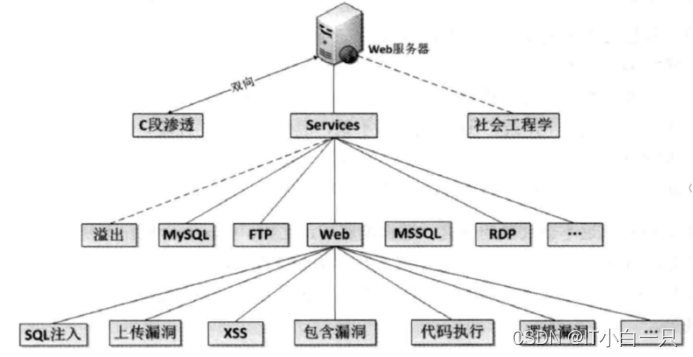
什么是C段渗透,C段就是和你同一个网段的一台主机,C段渗透就是通过和你同一网段的主机对你的目标ip进行ARP等手段进行渗透。
系统和web
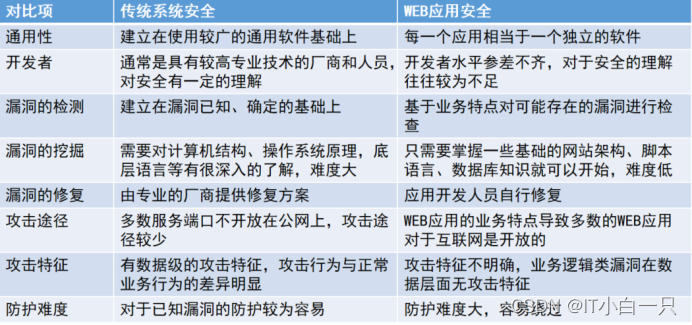
4.burpsute
burpsute原理
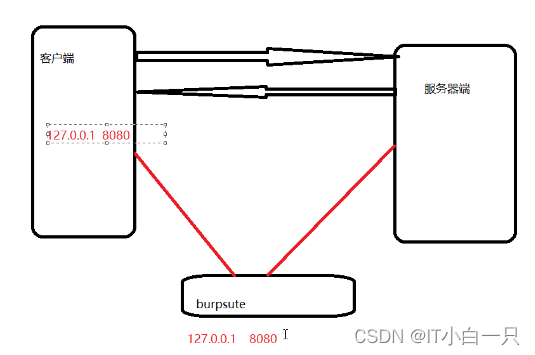
正常情况下客户端向服务器发送请求,但是加入burpsute工具,将浏览器端口和burpsute端口改为一致,可以对客户端发送的数据进行抓取。抓取信息之后可以进行数据的篡改。
下载安装FirFox,安装组件hacker,安装代理组件并配置
代理设置
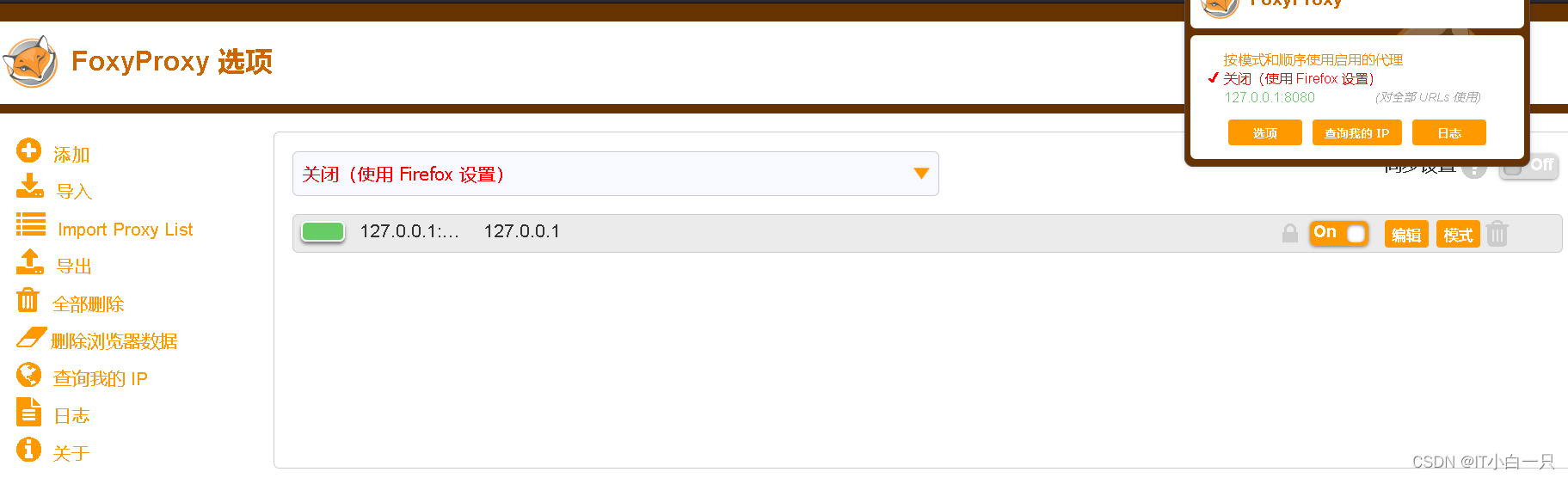
网址记录

漏洞和风险等级
praxy抓包模块
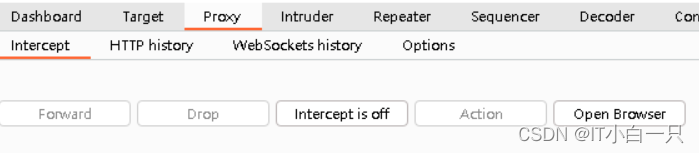
forward将数据包发送给服务器
drop丢掉不需要的数据包
intercept开始/结束抓包
Action/右键 可以发送给其他模块处理
Intruder暴力破解
repeater同一个数据包提交多次

Decoder加密解密

两个数据包对比
Extender安装插件

下午课程
brpsute篡改
更改信息
暴力破解
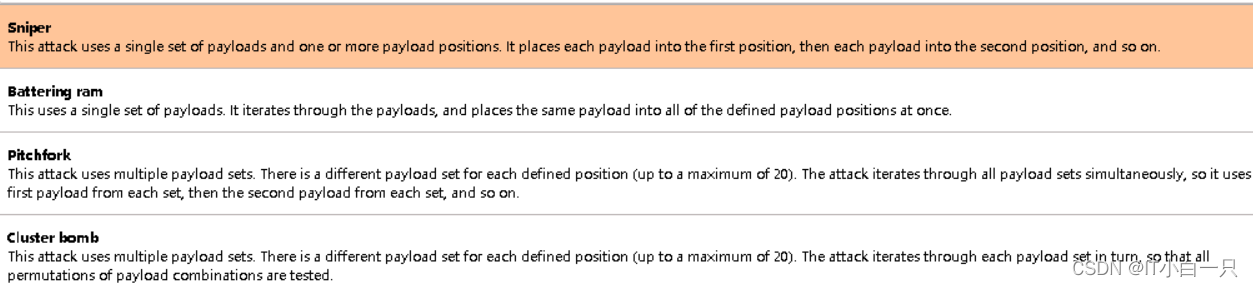
Sniper:只有一个暴力破解点
Battening:可以破解多个,但是必须破解的值是一样的
Pitchfork:多个破解点,但是破解的点之间是有联系的,字典匹配一一对应
Cluster bomb:多个破解,随机组合尝试,两个字典里面的数据随机组合,m*n
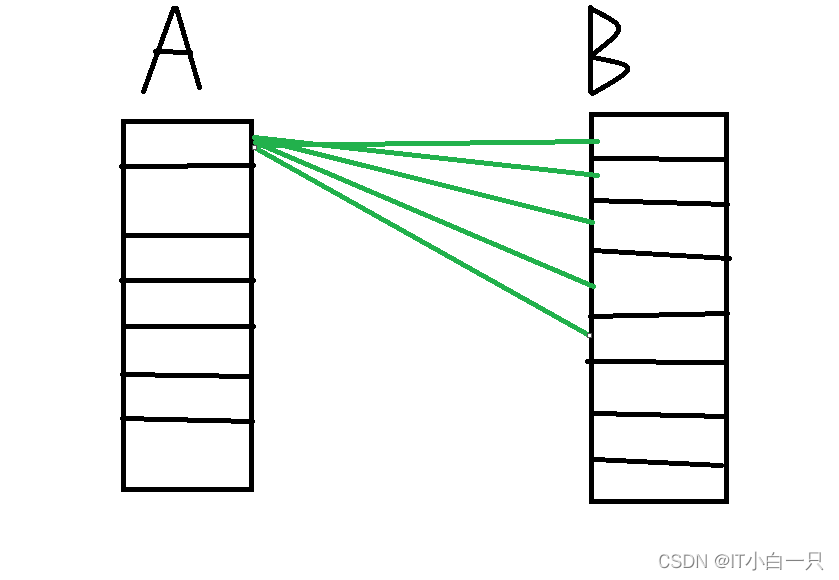
暴力破解将抓取到的数据包发送到Intruder,使用clear清除所有的破解点,选择自己需要破解的点进行Add添加,然后点击Payloads添加字典文件,可以手动添加常用的用户名和密码。开始破解等待结果,可以看Length,因为成功和失败响应的长度不一样,所以可以根据长度不一出现次数少的进行测试。还可以根据查看双击数据的具体,查看数据是否成功。
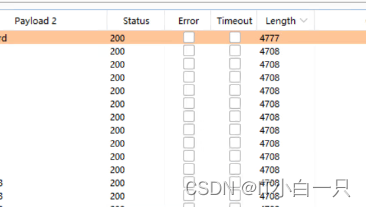
下午实操
这里是三个篡改,分别面对三个不同的场景,一种是篡改本地的地址,一种是篡改这里登录物理地址,一种是篡改浏览器版本
在这里插入图片描述

有验证码的暴力破解
首先新接触到了一个新的工具Pkav HTTP Fuzzer,这是一个针对有验证码专门破解 的工具,首先打开该软件运行,在需要验证码登录的网页复制该图片链接,并将该链接复制到图片验证码识别里面,测试是否可以识别出来。在重放选项里面将自动跟踪302重定向选中,因为网页的跳转会发生重定向。
在变体设置里面将该网页的网址复制在分析地址里面,使用burpsute攻击抓包,抓到之后将其放入到请求包中,对其登录名,密码,验证码进行添加破解设置,在右侧添加暴力破解的用户名和密码,然后再发包器中启动破解,通过对比长度可以发现哪一条数据是可以正确使用的。

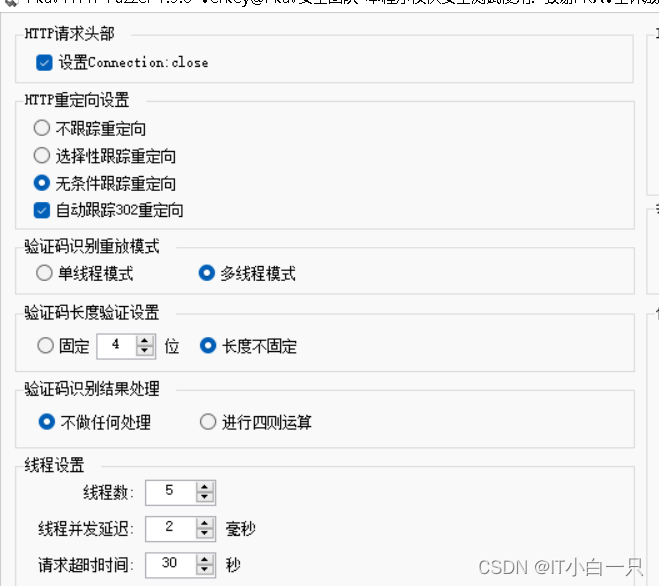
这种方式可以破解带有验证码的登录。