线性代数笔记5.3实对称矩阵的对角化

article/2025/9/22 14:42:51

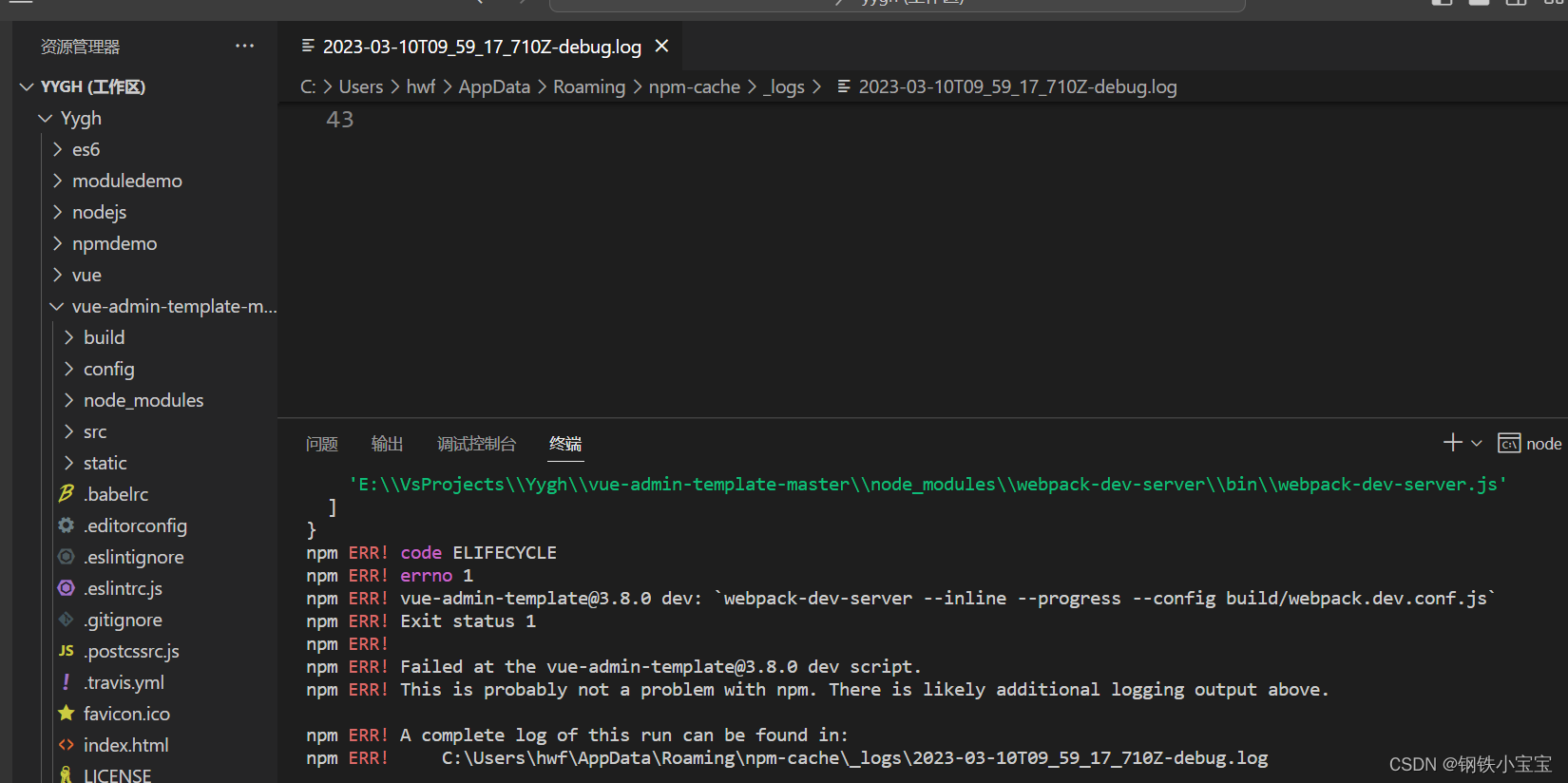
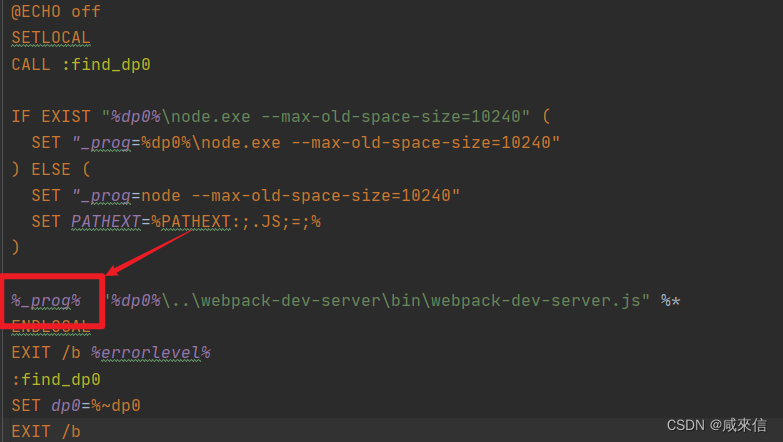
5.3实对称矩阵的对角化

正交矩阵

概念

A是一个n阶方阵 有A转置A == E，那么这个矩阵就是正交矩阵

性质

  1. 若A是正交矩阵，|A| == 1或 -1
  2. 若A是正交矩阵，A的逆 == A的转置 且A逆和A转置均为正交
  3. A,B正交，AB也正交
  4. 若A正交，α，β列向量 (Aα.Aβ) = (α.β)
    在这里插入图片描述

定理

A正交等价于A的列(行)向量组是标准正交向量组
在这里插入图片描述
例题

证|A| == 1且A是正交矩阵

看到aij == Aij这个时候就要使用伴随矩阵A*
在这里插入图片描述

实对称矩阵的对角化

定理

实对称矩阵A的不同特征值对应的特征向量一定正交

在这里插入图片描述

正交相似

在这里插入图片描述

解题步骤和方法

关键在第三步！！！！

在这里插入图片描述
是否使用施密特对角化的情况如下表

在这里插入图片描述
例题:
在这里插入图片描述
在这里插入图片描述


http://chatgpt.dhexx.cn/article/qU0Z2kmx.shtml

相关文章

实对称矩阵对角化为什么要做正交化单位化操作呢？

实对称矩阵对角化为什么要做正交化单位化操作呢？

今天晚上王小民同学问了助教姐姐一个问题，为什么对一个一般的矩阵对角化的时候，我们不用做正交单位化，对实对称矩阵对角化的时候却要做呢？这是一个很好的问题，所以和大家分享一下。 最后的结论就是：如果不…
阅读更多...
npm构建报错 code ELIFECYCLE解决办法

npm构建报错 code ELIFECYCLE解决办法

使用npm构建报错 code ELIFECYCLE 解决办法，进入工作目录 $ rm -rf node_modules $ rm -rf package-lock.json $ npm cache clear --force $ npm install
阅读更多...
code ELIFECYCLE npm ERR! errno 1

code ELIFECYCLE npm ERR! errno 1

最近遇到一个项目，npm下来报错errno -40048。 网上帖子有的说npm降级到5.3.0就行，试了直接errno -5 ，也还是不行。又有人说下载新的node.js覆盖就行，这里吐槽一下新版的node（node-v14.15.1-x64）&#xff0…
阅读更多...
npm ERR! code ELIFECYCLE报错解决

npm ERR! code ELIFECYCLE报错解决

最近多次遇到这个问题，然而网上的方法对我无效。。。 我是通过解决插件之间版本搭配问题来解决这个报错的，这一点我在博文webpack安装成功后的run build填坑之旅中也有写到，但可能内容太多，不显眼。。。 我本地的node.js是12.6.0c…
阅读更多...
Vue错误跳坑：npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! newbee@0.1.0 serve: `vue-cli-service serv

Vue错误跳坑：npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! newbee@0.1.0 serve: `vue-cli-service serv

废话不说，直接解决： 1、（别删除package.json，删除package-lock.json） 2、重新安装：npm install 重新安装后package-lock.json文件会重新生成 3、再次运行：npm run dev就成功了
阅读更多...
启动Vue项目报错“npm ERR! code ELIFECYCLE”

启动Vue项目报错“npm ERR! code ELIFECYCLE”

由于之前一直是npm和cnpm混着用，也没啥问题，今天在启动Vue项目的时候，却碰见了一个错误“npm ERR! code ELIFECYCLE”，一开始是用npm run启动的，后来换成cnpm run也不行。 查了一下资料，网上大多都说是因为…
阅读更多...
npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! test_vue_0613@1.0.0 dev: 错误的解决方法

npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! test_vue_0613@1.0.0 dev: 错误的解决方法

在命令行中使用命令 npm run dev运行从网上下载的一个vue项目时出现了以下报错 npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! test_vue_06131.0.0 dev: node build/dev-server.js npm ERR! Exit status 1 npm ERR! npm ERR! Failed at the test_vue_06131.0.0 dev scri…
阅读更多...
npm ERR! code ELIFECYCLE的解决

npm ERR! code ELIFECYCLE的解决

在使用npm run dev启动程序时，报出如下错误： npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! datav.jiaminghi.com2.0.0 dev: vuepress dev docs npm ERR! Exit status 1 npm ERR! npm ERR! Failed at the datav.jiaminghi.com2.0.0 dev script.…
阅读更多...
vue运行报错npm ERR! code ELIFECYCLE npm ERR! errno 9009

vue运行报错npm ERR! code ELIFECYCLE npm ERR! errno 9009

项目场景： 最近写代码VScode终端运行项目过程中出现中断运行的情况，人狠话不多，直接上报错图，如下 问题描述 原因分析： 刚开始其实是报134，后来查资料捣鼓了半天开始报9009，不过参阅资料表示本…
阅读更多...
VUE项目执行npm run dev报错 npm ERR! code ELIFECYCLE npm ERR! errno 134 npm ERR wisdom-shipping-agent.....

VUE项目执行npm run dev报错 npm ERR! code ELIFECYCLE npm ERR! errno 134 npm ERR wisdom-shipping-agent.....

完整报错如下： 纯后端选手，拉前端代码方便自测，遇到如下问题，搜集资料得以解决，记录一下！ 原因：内存溢出 解决办法： 1.进入工程目录下执行命令： npm install -g incr…
阅读更多...
webstorm打包，运行package.json时，dev出现code ELIFECYCLE问题如下图

webstorm打包，运行package.json时，dev出现code ELIFECYCLE问题如下图

先看自己是否安装成功node.js 进入黑窗口输入node -v查看node.js版本 npm -v查看npm版本 webpack查看是否安装成功 webpack -v查看 查询安装成功，已配置 查询任务管理器发现node.js未启动，重启node.js解决问题。
阅读更多...
npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! vue-ts-vite@0.0.0 dev: `vite` npm ERR! Exit statu

npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! vue-ts-vite@0.0.0 dev: `vite` npm ERR! Exit statu

一、先看报错 报错截图： 报错信息： npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! vue-ts-vite0.0.0 dev: vite npm ERR! Exit status 1 npm ERR! npm ERR! Failed at the vue-ts-vite0.0.0 dev script. npm ERR! This is probably not a pro…
阅读更多...
code ELIFECYCLE

code ELIFECYCLE

VS Code 上传到远程仓库报错，错误信息如下： 查看日志，这个是由于安装node_modules时候部分依赖包没有下载，运行 npm install typescript-eslint/eslint-pluginlatest --save-dev 安装缺失的依赖。 或删除yarn.lock文件和node_mo…
阅读更多...
【问题解决】npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! newbee@0.1.0 serve: `vue-cli-service serv

【问题解决】npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! newbee@0.1.0 serve: `vue-cli-service serv

Plan 在本地运行ids项目. Do 执行npm run serve,报如下错误 npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! newbee0.1.0 serve: vue-cli-service serve npm ERR! Exit status 1 npm ERR! npm ERR! Failed at the newbee0.1.0 serve script. npm ERR! This is probab…
阅读更多...
解决：npm ERR code ELIFECYCLE npm ERR errno 1(安装脚手架过程中，在npm run dev 时发生错误)

解决：npm ERR code ELIFECYCLE npm ERR errno 1(安装脚手架过程中，在npm run dev 时发生错误)

解决：npmERR! code ELIFECYCLEnpm ERR! errno 1问题 今天在自己学习react时候遇到了一个问题，就是在自己执行npm start运行项目时，产生了如下报错，在vue3也可以同样适用删掉node_modules重新按一边，再 npm i 一下即可…
阅读更多...
解决：npm ERR! code ELIFECYCLE npm ERR! errno 1

解决：npm ERR! code ELIFECYCLE npm ERR! errno 1

解决：npm ERR! code ELIFECYCLEnpm ERR! errno 1问题 今天在自己学习react时候遇到了一个问题，就是在自己执行npm start运行项目时，产生了如下报错 然后我自己稀里糊涂的弄了好几遍，瞎弄一通，只会产生更多的报错。最…
阅读更多...
npm ERR code ELIFECYCLEnpm ERR errno 1报错

npm ERR code ELIFECYCLEnpm ERR errno 1报错

解决 ：在文件，端口都无变换的情况下 可能是环境变量的path丢失了
阅读更多...
ELIFECYCLECommand failed with exit code 1

ELIFECYCLECommand failed with exit code 1

提示找不到模块： 删除node_modules包 重新下载包 可解决
阅读更多...
JAVA动态绑定机制

JAVA动态绑定机制

JAVA动态绑定机制（非常非常重要） JAVA动态绑定机制：动态绑定是与运行类型进行绑定 1.当调用对象方法的时候，该方法会和该对象的内存地址/运行类型（也就是与运行类型）绑定（意思就是如&#xff…
阅读更多...
动态绑定多个值

动态绑定多个值

React 属性展开 如果你已经有了一个 props 对象&#xff0c;你可以使用展开运算符 ... 来在 JSX 中传递整个 props 对象。以下两个组件是等价的&#xff1a; function App1() {return <Greeting firstName"Ben" lastName"Hector" />; }function App2…
阅读更多...
推荐文章

Copyright @ 2022~2023