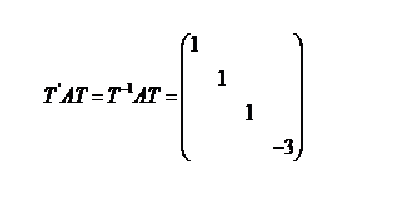矩阵的相似对角化

article/2025/9/22 14:36:20

矩阵相似的定义

设 A与B都是N阶方阵，若是 $\exists$ 一个可逆的N阶矩阵P，使得 $P^{-1}AP=B$ ，则称A与B相似，记作 $A\sim B$ ，P成为由A到B的相似变换矩阵

相似矩阵的性质

1、 $A\sim A \because E^{-1}AE=A$

矩阵A与它自身相似

2、若 $A\sim B$ ，则 $B\sim A$

如果A与B相似，那么B与A也相似

证明： $\because A\sim B$

$\therefore P^{-1}AP=B\rightarrow PBP^{-1}=A$

所以 $P^{-1}$ 为B到A的相似变换矩阵

3、若 $A\sim B,B\sim C$ ，则 $A\sim C$

相似具有传递性

证明： $\because A\sim B,B\sim C$

$\therefore P^{-1}AP=B , Q^{-1}BQ=C$

将A代换B

$Q^{-1}P^{-1}APQ=C\rightarrow (PQ)^{-1}A(PQ)=C$

其中 $PQ$ 为A到C的相似变换矩阵

4、若 $A\sim B$ ，则 $A\cong B$

如果A和B相似，那么A与B等价

因为等价的定义是 $PAQ=B$ ，存在P、Q使得A经过有限次的初等变换，成为B，那么称A与B等价

所以上述明显成立

也意味着，A和B两个矩阵的秩是一样的

5、若 $A\sim B$ ，则 $\left | A-\lambda E \right |=\left | B-\lambda E \right |$ ，意味着如果两个矩阵相似，那么他们的特征值相同，因为特征值相同，所以两个矩阵的迹+行列式都相同

证明： $\because A\sim B$

$\therefore P^{-1}AP=B\rightarrow \left | A-\lambda E \right |\rightarrow \left | P^{-1}AP-\lambda P^{-1}P \right | \rightarrow \left | P^{-1}(A-\lambda E) P \right |\rightarrow \left | P^{-1} \right |\left | P \right |\left | (A-\lambda E) \right |\rightarrow 1*\left | (A-\lambda E) \right |$

6、若 $A\sim B$ ， $A^{-1}\sim B^{-1}$

如果A、B相似，那么A的逆和B的逆也相似

证明： $P^{-1}AP=B\rightarrow A=PBP^{-1}\rightarrow A^{-1}=PB^{-1}P^{-1}\rightarrow P^{-1}A^{-1}P=B^{-1}$

所以， $A^{-1}\sim B^{-1}$

7、若 $A\sim B$ ， $A^{*}\sim B^{*}$

如果A、B相似，那么A的伴随矩阵和B的伴随矩阵也相似

证明： $\left | A \right |A^{-1}=A^{*}$

因为A、B相似，那么A、B的行列式相同

由6可知，A的逆与B的逆也相似

$P^{-1}\left | A \right |A^{-1}P=\left | A \right |B^{-1}=\left | B \right |B^{-1}$

$P^{-1}A^{*}P=B^{*}$

所以A的伴随跟B的伴随也相似

8、若 $A\sim B$ ， $kA\sim kB$

如果A、B相似，那么kA与kB也相似

证明：这个很简单

$A\sim B\rightarrow P^{-1}AP=B\rightarrow P^{-1}(kA)P=(kB)$

9、若 $A\sim B$ ， $A^{k}\sim B^{k}$

如何A、B相似，那么A的k次方与B的k次方也相似

证明：

$P^{-1}AP=B$

$B^{k}=(P^{-1}AP)^{k}=\underset{k}{\underbrace{P^{-1}APP^{-1}AP...P^{-1}AP}}=P^{-1}A^{k}P$

$\therefore P^{-1}A^{k}P=B^{k}$

10、若 $A\sim B$ ， $f(A)\sim f(B)$ ，其中f(x)为多项式

如果A矩阵与B矩阵相似，那么A矩阵的多项式与B矩阵的多项式也相似

证明：

设 $f(x)=a_{n}x^{n}+a_{n-1}x^{n-1}....+a_{2}x^{2}+a_{1}x$

根据8+9的性质，就能证明该性质

11、若 $A\sim B$ ， $A^{T}\sim B^{T}$

如果A、B相似，那么A的转置和B的转置也相似

证明：

$P^{-1}AP=B$

$B^{T}=P^{T}A(P^{T})^{-1}$

$A=PBP^{-1}\rightarrow A^{T}=\rightarrow (P^{T})^{-1}P^{-1}APP^{T}$

$PP^{T} A^{T}(P^{T})^{-1}P^{-1}=\rightarrow A$

将之代入到 $B^{T}=P^{T}A(P^{T})^{-1}$

$B^{T}=P^{T}PP^{T} A^{T}(P^{T})^{-1}P^{-1}(P^{T})^{-1}$

$P^{T}PP^{T} A^{T}(P^{T}PP^{T})^{-1}=B^{T}\rightarrow ((P^{T}PP^{T})^{-1})^{-1}A^{T}(P^{T}PP^{T})^{-1}=B^{T}$

矩阵的相似对角化定义

其实就是 $P^{-1}AP=B$ 中的B为对角矩阵（diag），或者称之为 $\Lambda$ ，如果不存在矩阵P使得A可以变成对角矩阵，那么就称A不能相似对角化

两个问题，什么样的A可以相似对角化？A如果可以相似对角化，那么 $\Lambda$ 是多少？

设 $P^{-1}AP=\Lambda$

其中 $\Lambda = \begin{vmatrix} \lambda _{1}& & & \\ & \lambda _{2}& & \\ & & ...& \\ & & & \lambda _{n} \end{vmatrix}$

设 $P=\begin{vmatrix} \alpha _{1} & \alpha _{2} & ...& \alpha _{n} \end{vmatrix}$ ，其中 $\alpha _{1},\alpha _{2}...\alpha _{n}$ 为n维的列向量

代入等式

$P^{-1}AP=\Lambda\rightarrow AP=P\Lambda$

$A\begin{vmatrix} \alpha _{1} & \alpha _{2} & ...& \alpha _{n} \end{vmatrix}=\begin{vmatrix} \alpha _{1} & \alpha _{2} & ...& \alpha _{n} \end{vmatrix}\begin{vmatrix} \lambda _{1}& & & \\ & \lambda _{2}& & \\ & & ...& \\ & & & \lambda _{n} \end{vmatrix}$

$\begin{vmatrix} A\alpha _{1} & A\alpha _{2} & ...& A\alpha _{n} \end{vmatrix}=\begin{vmatrix} \alpha _{1}\lambda _{1} & \alpha _{2}\lambda _{2} & ...& \alpha _{n}\lambda _{n} \end{vmatrix}$