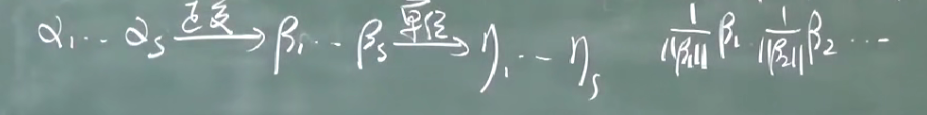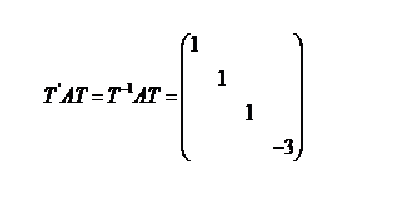线性代数笔记5.3实对称矩阵的对角化（前瞻知识）

article/2025/9/22 14:01:29

实对称矩阵都能对角化

内积

简单来说，内积就是两个向量的对应分量相乘再相加

内积是个数！！
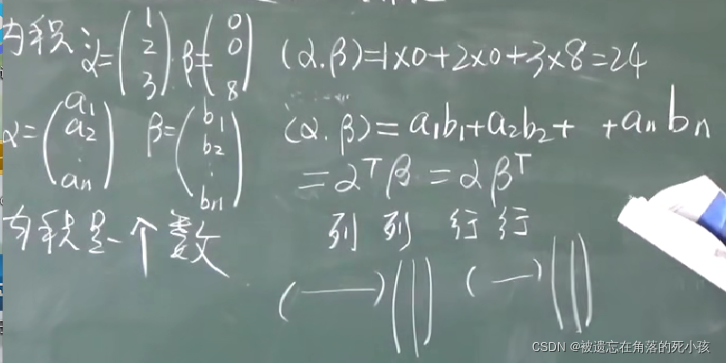
在这里插入图片描述

内积的性质

注意最后一条性质

两个向量和与第三个向量的内积 == 两个向量分别与第三个向量内积的和，这条性质可以与上面的性质配合使用
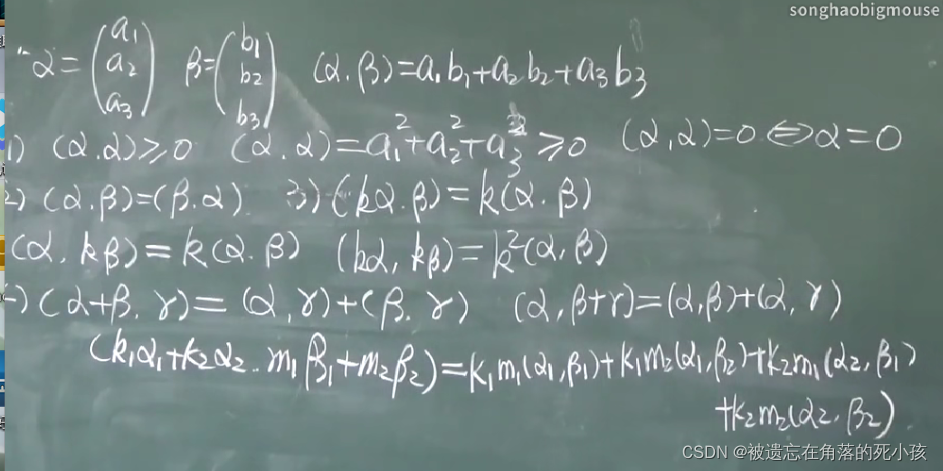
在这里插入图片描述

（向量）长度

向量的长度等于与它自己做内积再开根号，即点到原点的距离

若向量长度 == 1，则这个向量称为单位向量

单位化

有些向量长度并不是1，但是可以通过化简让它的长度变为1

方法：乘长度分之一

性质

  1. 向量的长度 >= 0 ||a|| == 0 等价于 a == 0
  2. 在长度运算里外提一个数，这个数需要加绝对值

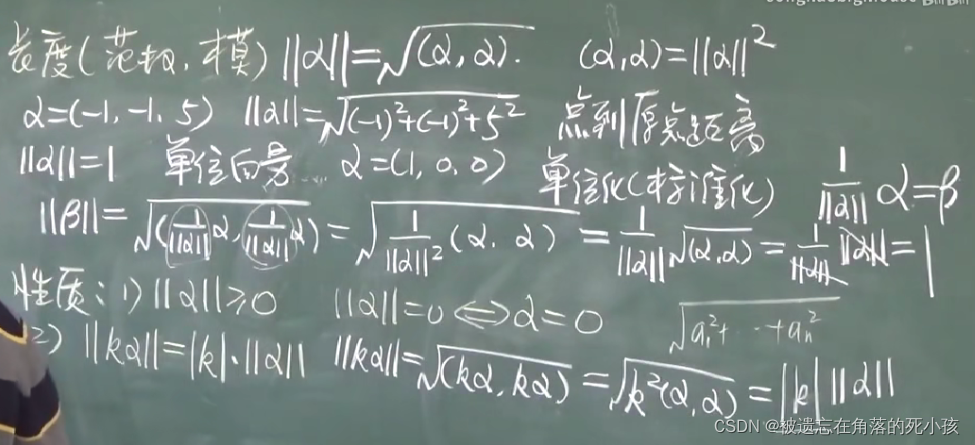
在这里插入图片描述
3. 两个向量的内积 <= 两个向量的长度相乘
4. 两个向量相加后的长度 <= 两个向量的长度再相加 (三角不等式)
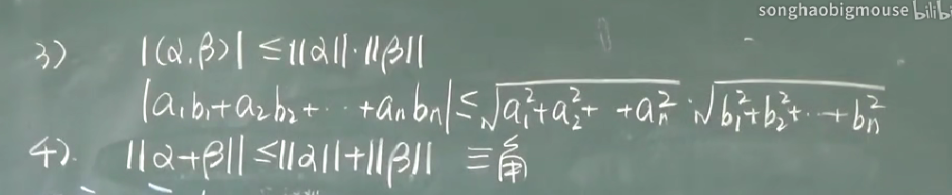
在这里插入图片描述

正交

两个向量内积 == 0 记作 α⊥β 和自身正交等于0的向量只能是0向量

零向量与任意向量都正交

正交向量组

不含0向量的向量组，向量组内的向量两两正交

标准正交向量组

向量组里的向量和自己做内积时 = 1 和别人做内积的时候 = 0
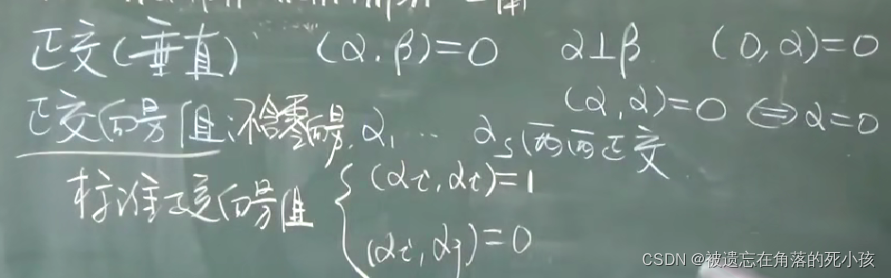
在这里插入图片描述

定理

在这里插入图片描述
反过来不一定成立！！

施密特正交化

在这里插入图片描述
在这里插入图片描述


http://chatgpt.dhexx.cn/article/apsB8uUo.shtml

相关文章

含重根的三阶实对称矩阵的快速对角化方法

含重根的三阶实对称矩阵的快速对角化方法

众所周知&#xff0c;实对称矩阵一定可以相似对角化。而考试中考察的三阶实对称矩阵对角化基本都是三阶的。而且正常情况下特征根一定是整数。因此基于此&#xff0c;有一些特殊的方法可以快速计算三阶实对称矩阵的特征值和特征向量。 一. 猜根法计算特征值 特征值之和等于矩阵…
阅读更多...
矩阵的相似对角化

矩阵的相似对角化

矩阵相似的定义 设 A与B都是N阶方阵&#xff0c;若是一个可逆的N阶矩阵P&#xff0c;使得&#xff0c;则称A与B相似&#xff0c;记作&#xff0c;P成为由A到B的相似变换矩阵 相似矩阵的性质 1、 矩阵A与它自身相似 2、若&#xff0c;则 如果A与B相似&#xff0c;那么B与A…
阅读更多...
矩阵对角化

矩阵对角化

一、矩阵对角化的理论 一个映射或者一个线性变换&#xff0c;都有一个矩阵和它相对应。矩阵或者映射是不是可以对角化&#xff0c;对工程应用来说比较重要&#xff0c;因为对角化后的矩阵&#xff0c;乘积简单&#xff0c;经过多次变换的话&#xff0c;相当于矩阵的多次方。矩…
阅读更多...
实对称矩阵必可正交对角化证明

实对称矩阵必可正交对角化证明

我的小程序&#xff1a; 待办计划&#xff1a;给自己立个小目标吧&#xff01; n阶矩阵A可正交对角化的充分条件是A是实对称矩阵&#xff0c;即若A是实对称矩阵则A必可正交对角化。 首先&#xff0c;有以下定理&#xff1a; 若的特征值为&#xff0c;且&#xff0c;则存在正交…
阅读更多...
实对称阵的正交相似对角化

实对称阵的正交相似对角化

一、正交向量组与正交矩阵 正交向量组的定义&#xff0c;是一组非零向量&#xff0c;且两两正交&#xff0c;那么这组向量&#xff0c;则成为正交向量组。 两个向量正交的意思是&#xff0c;两个向量的内积为0&#xff0c;什么是两个向量的内积&#xff0c;就是向量内对应元素…
阅读更多...
线性代数笔记5.3实对称矩阵的对角化

线性代数笔记5.3实对称矩阵的对角化

5.3实对称矩阵的对角化 正交矩阵 概念 A是一个n阶方阵 有A转置A E&#xff0c;那么这个矩阵就是正交矩阵 性质 若A是正交矩阵&#xff0c;|A| 1或 -1若A是正交矩阵&#xff0c;A的逆 A的转置 且A逆和A转置均为正交A,B正交&#xff0c;AB也正交若A正交&#xff0c;α&am…
阅读更多...
实对称矩阵对角化为什么要做正交化单位化操作呢？

实对称矩阵对角化为什么要做正交化单位化操作呢？

今天晚上王小民同学问了助教姐姐一个问题&#xff0c;为什么对一个一般的矩阵对角化的时候&#xff0c;我们不用做正交单位化&#xff0c;对实对称矩阵对角化的时候却要做呢&#xff1f;这是一个很好的问题&#xff0c;所以和大家分享一下。 最后的结论就是&#xff1a;如果不…
阅读更多...
npm构建报错 code ELIFECYCLE解决办法

npm构建报错 code ELIFECYCLE解决办法

使用npm构建报错 code ELIFECYCLE 解决办法&#xff0c;进入工作目录 $ rm -rf node_modules $ rm -rf package-lock.json $ npm cache clear --force $ npm install
阅读更多...
code ELIFECYCLE npm ERR! errno 1

code ELIFECYCLE npm ERR! errno 1

最近遇到一个项目&#xff0c;npm下来报错errno -40048。 网上帖子有的说npm降级到5.3.0就行&#xff0c;试了直接errno -5 &#xff0c;也还是不行。又有人说下载新的node.js覆盖就行&#xff0c;这里吐槽一下新版的node&#xff08;node-v14.15.1-x64&#xff09;&#xff0…
阅读更多...
npm ERR! code ELIFECYCLE报错解决

npm ERR! code ELIFECYCLE报错解决

最近多次遇到这个问题&#xff0c;然而网上的方法对我无效。。。 我是通过解决插件之间版本搭配问题来解决这个报错的&#xff0c;这一点我在博文webpack安装成功后的run build填坑之旅中也有写到&#xff0c;但可能内容太多&#xff0c;不显眼。。。 我本地的node.js是12.6.0c…
阅读更多...
Vue错误跳坑：npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! newbee@0.1.0 serve: `vue-cli-service serv

Vue错误跳坑：npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! newbee@0.1.0 serve: `vue-cli-service serv

废话不说&#xff0c;直接解决&#xff1a; 1、&#xff08;别删除package.json&#xff0c;删除package-lock.json&#xff09; 2、重新安装&#xff1a;npm install 重新安装后package-lock.json文件会重新生成 3、再次运行&#xff1a;npm run dev就成功了
阅读更多...
启动Vue项目报错“npm ERR! code ELIFECYCLE”

启动Vue项目报错“npm ERR! code ELIFECYCLE”

由于之前一直是npm和cnpm混着用&#xff0c;也没啥问题&#xff0c;今天在启动Vue项目的时候&#xff0c;却碰见了一个错误“npm ERR! code ELIFECYCLE”&#xff0c;一开始是用npm run启动的&#xff0c;后来换成cnpm run也不行。 查了一下资料&#xff0c;网上大多都说是因为…
阅读更多...
npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! test_vue_0613@1.0.0 dev: 错误的解决方法

npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! test_vue_0613@1.0.0 dev: 错误的解决方法

在命令行中使用命令 npm run dev运行从网上下载的一个vue项目时出现了以下报错 npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! test_vue_06131.0.0 dev: node build/dev-server.js npm ERR! Exit status 1 npm ERR! npm ERR! Failed at the test_vue_06131.0.0 dev scri…
阅读更多...
npm ERR! code ELIFECYCLE的解决

npm ERR! code ELIFECYCLE的解决

在使用npm run dev启动程序时&#xff0c;报出如下错误&#xff1a; npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! datav.jiaminghi.com2.0.0 dev: vuepress dev docs npm ERR! Exit status 1 npm ERR! npm ERR! Failed at the datav.jiaminghi.com2.0.0 dev script.…
阅读更多...
vue运行报错npm ERR! code ELIFECYCLE npm ERR! errno 9009

vue运行报错npm ERR! code ELIFECYCLE npm ERR! errno 9009

项目场景&#xff1a; 最近写代码VScode终端运行项目过程中出现中断运行的情况&#xff0c;人狠话不多&#xff0c;直接上报错图&#xff0c;如下 问题描述 原因分析&#xff1a; 刚开始其实是报134&#xff0c;后来查资料捣鼓了半天开始报9009&#xff0c;不过参阅资料表示本…
阅读更多...
VUE项目执行npm run dev报错 npm ERR! code ELIFECYCLE npm ERR! errno 134 npm ERR wisdom-shipping-agent.....

VUE项目执行npm run dev报错 npm ERR! code ELIFECYCLE npm ERR! errno 134 npm ERR wisdom-shipping-agent.....

完整报错如下&#xff1a; 纯后端选手&#xff0c;拉前端代码方便自测&#xff0c;遇到如下问题&#xff0c;搜集资料得以解决&#xff0c;记录一下&#xff01; 原因&#xff1a;内存溢出 解决办法&#xff1a; 1.进入工程目录下执行命令&#xff1a; npm install -g incr…
阅读更多...
webstorm打包，运行package.json时，dev出现code ELIFECYCLE问题如下图

webstorm打包，运行package.json时，dev出现code ELIFECYCLE问题如下图

先看自己是否安装成功node.js 进入黑窗口输入node -v查看node.js版本 npm -v查看npm版本 webpack查看是否安装成功 webpack -v查看 查询安装成功&#xff0c;已配置 查询任务管理器发现node.js未启动&#xff0c;重启node.js解决问题。
阅读更多...
npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! vue-ts-vite@0.0.0 dev: `vite` npm ERR! Exit statu

npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! vue-ts-vite@0.0.0 dev: `vite` npm ERR! Exit statu

一、先看报错 报错截图&#xff1a; 报错信息&#xff1a; npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! vue-ts-vite0.0.0 dev: vite npm ERR! Exit status 1 npm ERR! npm ERR! Failed at the vue-ts-vite0.0.0 dev script. npm ERR! This is probably not a pro…
阅读更多...
code ELIFECYCLE

code ELIFECYCLE

VS Code 上传到远程仓库报错&#xff0c;错误信息如下&#xff1a; 查看日志&#xff0c;这个是由于安装node_modules时候部分依赖包没有下载&#xff0c;运行 npm install typescript-eslint/eslint-pluginlatest --save-dev 安装缺失的依赖。 或删除yarn.lock文件和node_mo…
阅读更多...
【问题解决】npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! newbee@0.1.0 serve: `vue-cli-service serv

【问题解决】npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! newbee@0.1.0 serve: `vue-cli-service serv

Plan 在本地运行ids项目. Do 执行npm run serve,报如下错误 npm ERR! code ELIFECYCLE npm ERR! errno 1 npm ERR! newbee0.1.0 serve: vue-cli-service serve npm ERR! Exit status 1 npm ERR! npm ERR! Failed at the newbee0.1.0 serve script. npm ERR! This is probab…
阅读更多...
推荐文章

Copyright @ 2022~2023