今天开始正式进入微信小程序端的开发,由于本人从未学习过小程序开发,所以在此一并把学习过程记录。
安装微信开发者工具,以非云开发的基础模板创建文件,得到如下项目结构:
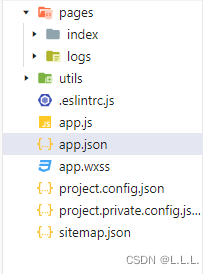
page即为页面,目前有两个文件夹:index和logs,即为首页和日志。
utils即为公共文件夹,存放公共的文件,不是必要存在的。
app开头的文件都是全局的:
app.js是入口文件(js文件都是负责逻辑的)。
app.json是配置文件(json都是负责配置项的)。
app.wxss类似于css文件,是个样式文件。
index下的文件也类似,wxml即对应前端的html文件。
project.config.json文件为项目配置文件,做一些个性化的配置,例如界面颜色、编译配置等等。
sitemap.json是小程序的索引文件,类似于网站地图文件。
对于开发相对重要的文件是page,app.json和app.wxss。
先看看index.wxml文件:
即为
增加修改一个文本块(我不知道怎么描述这个),可以采用与div类似的用法:
在wxml中:耗材管理系统
在wxss中:.box{width:100px; height:100px; background: red;}
即可实现此效果:

这对于熟悉html开发的程序员可以说是很方便了(但我连html也不会( _))
那怎么看到logs页面呢?打开app.json调整目录结构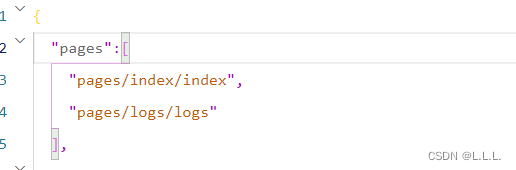
把"page/logs/logs"放到上面即可。
如何创建一个新文件呢?一种方法是在pages文件夹下创建新文件夹,并在目录下“新建page”即可,另一种方法,更为通用的方法是,在上面的app.json中,“pages”:[]中,仿照index和logs输入“pages/new/new"即可自动创建新页面。