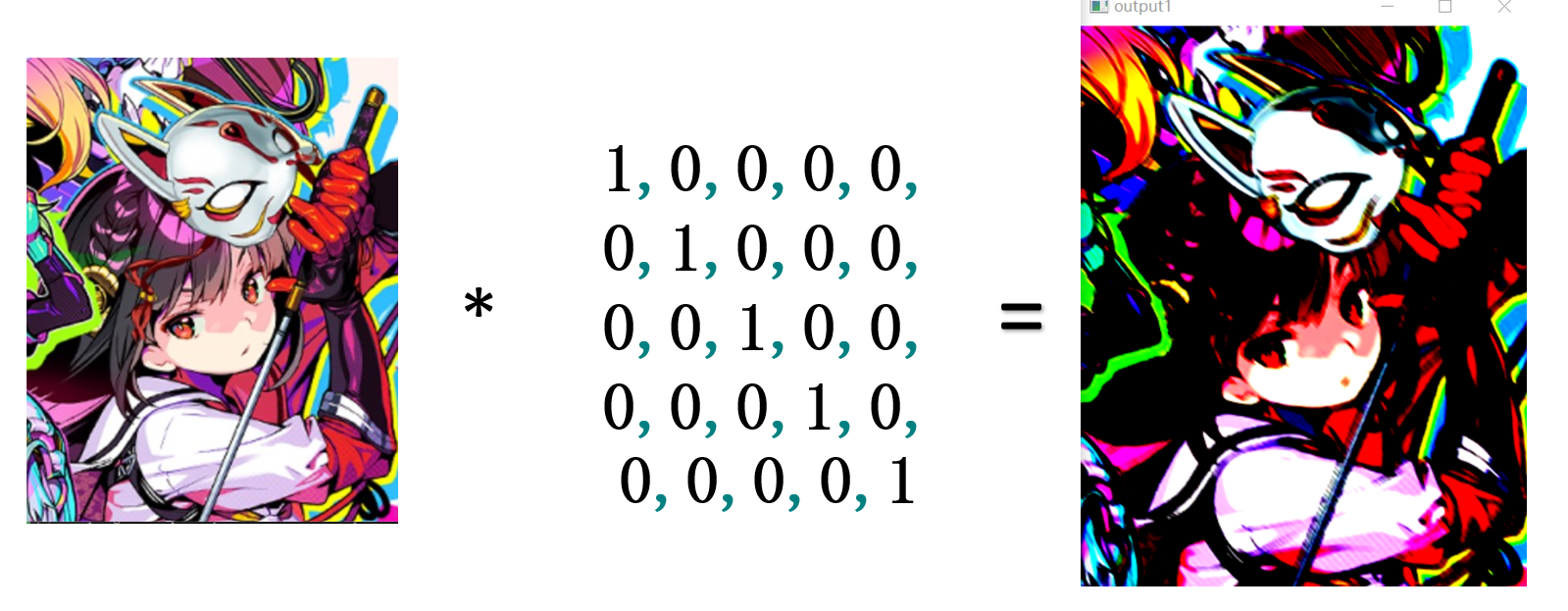
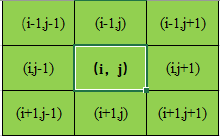
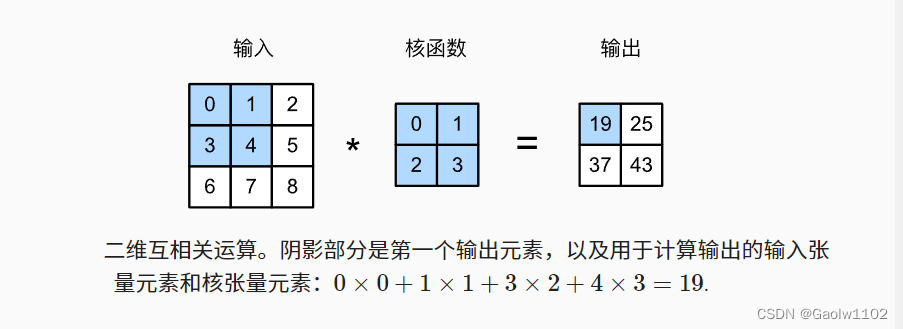
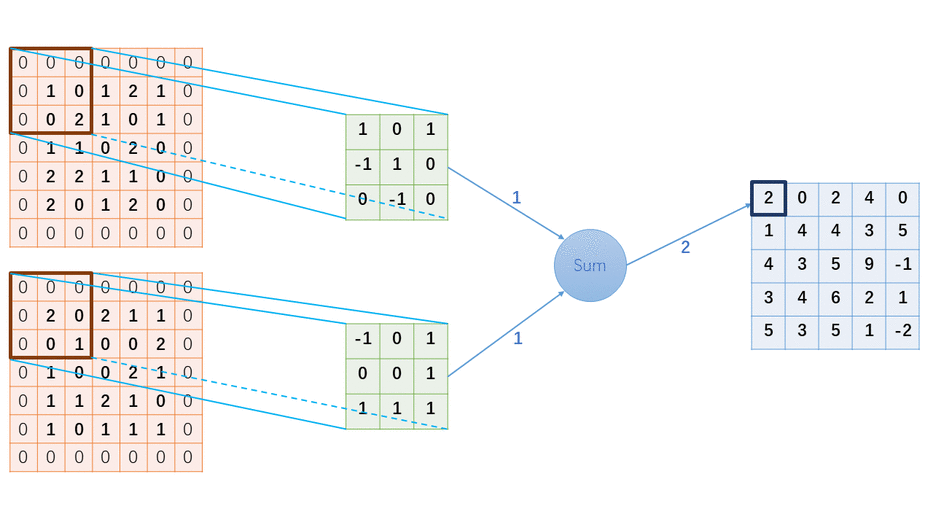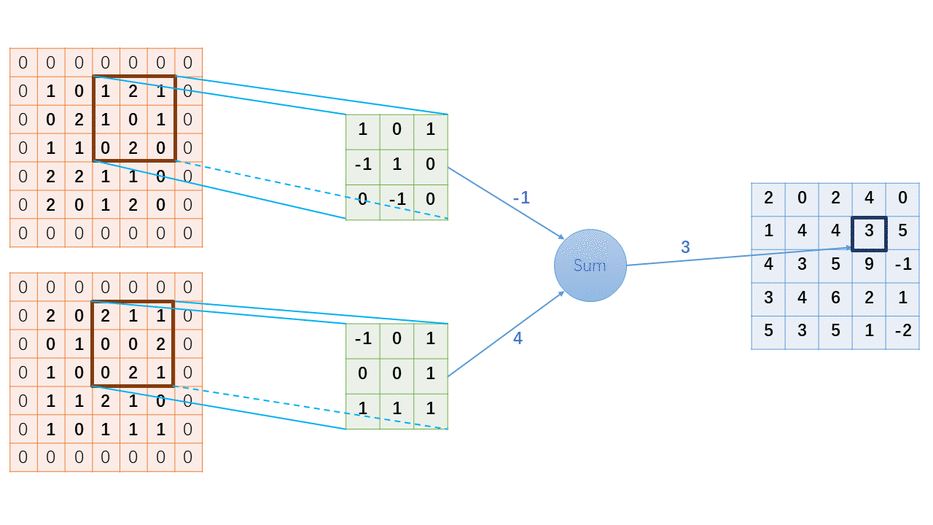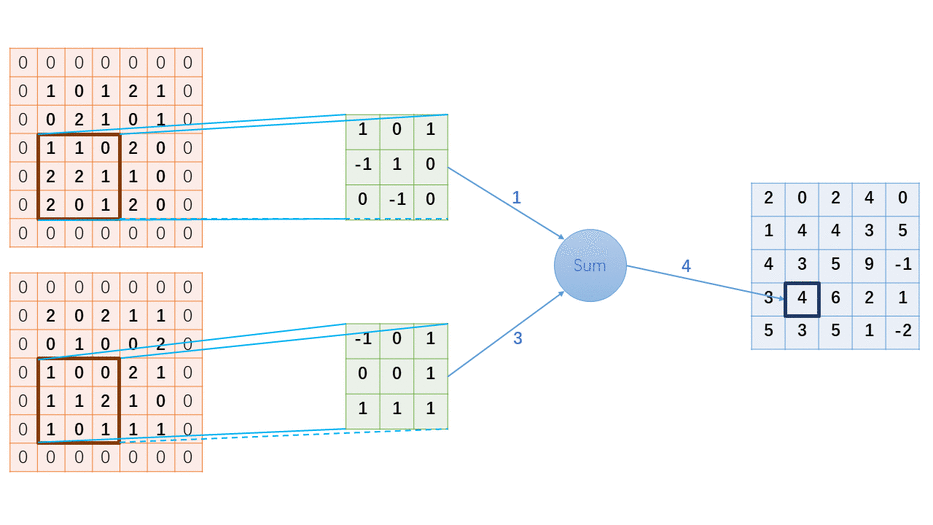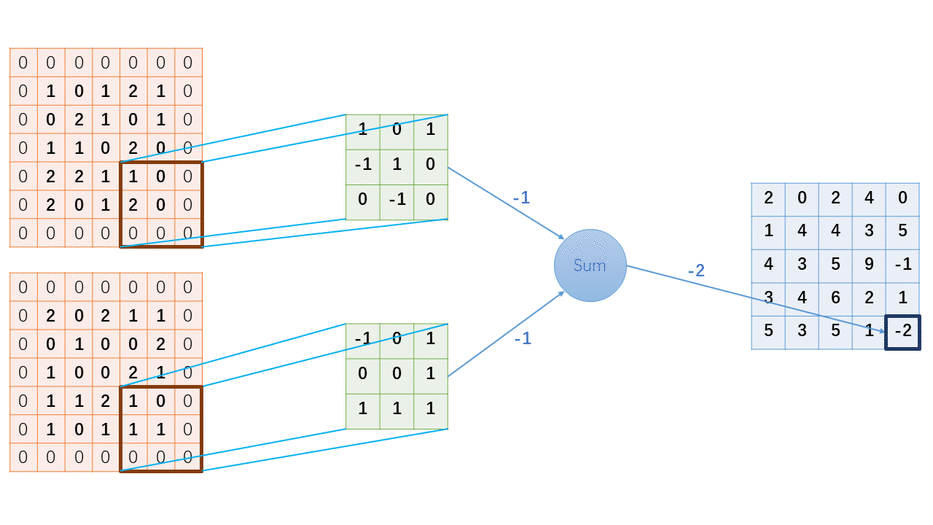
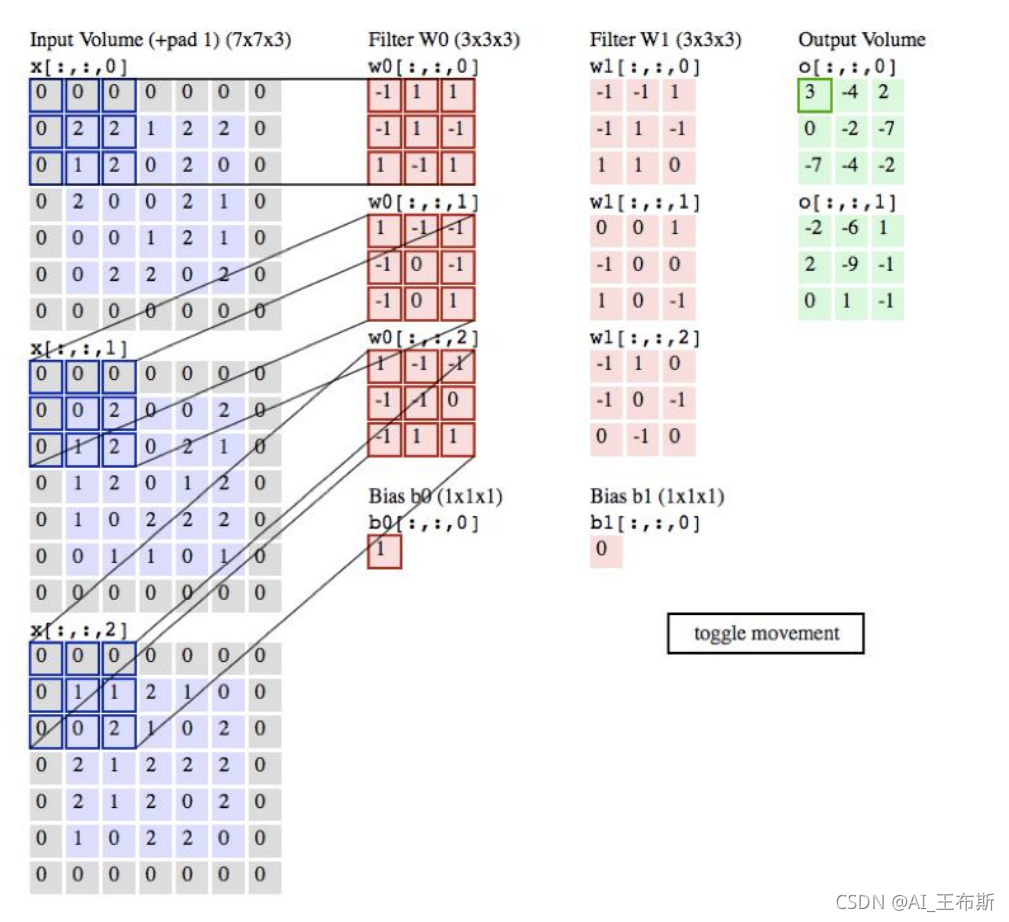
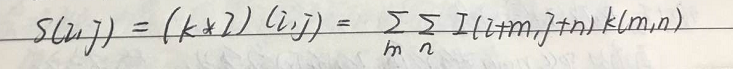卷积神经网络用的其实不是卷积运算,实际用的是互相关运算;互相关运算和卷积运算的区别在于对输入结果所加的权重系数的顺序不同而已,但由于神经网络本身就是训练参数的,所以两者的输出结果其实是一样的,而互相关运算相比卷积运算由于权重系数(卷积核)无需翻转,更加简单,所以实际的卷积网络都是基于互相关运算的;
互相关运算和卷积一维计算原理:
这里先从一维的开始介绍,方便大家理解;给定一维序列和一维序列
,
则互相关序列为:
其中的元素为:
对于卷积序列为:
其中的元素为:
这里举例来解释什么意思:假设序列,
省略号表示后面都是0,因为一般来说,权重序列和输入矩阵都是稀疏矩阵;
那么互相关运算满足:

对于上述互相关运算的第i个元素会等于序列W的第
个元素w[
]和序列X的第
个元素x
相乘再相加,其中
以上面公式1的第二行为例,此时i=-2, 先看W序列和X序列的元素序号,找到
的所有组合:ix=0时,iw=2;ix=1时,iw=3,由于w[3]=0,而且后续因为都是0,所以对于
只有
这一项;
再以公式1的第三行为例,,此时i=-1, 先看W序列和X序列的元素序号,找到
的所有组合:ix=0时,iw=1,则;ix=1时,iw=2;ix=2时,iw=3,由于w[3]=0,而且后续因为都是0,所以对于
有
,
共两项;后续就不在介绍了,大家可以自行推导;
对于卷积运算则是:

对于上述卷积运算的第i个元素会等于W序列的第
个元素w[
]和序列X的第
个元素x[
]相乘再相加,其中
,
以公式2第3行为例,,此时i=1, 先看W序列和X序列的元素序号,找到
的所有组合:ix=0时,iw=1,则;ix=1时,iw=0;ix=2时,iw=-1,由于w[-1]=0,而且后续因为都是0,所以对于
有
,
这两项;一次类推,大家可以试试其它行,结果都符合上述规则,这里就不再推导;
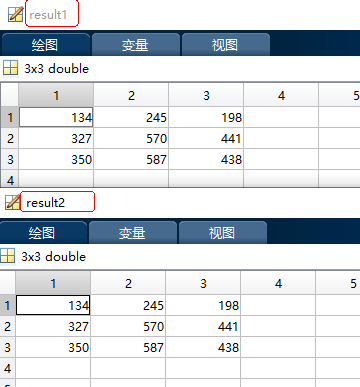
总的来说,比较互相关运算和卷积运算,可以发现他们唯一的区别就在于X序列前面的W序列的顺序刚好相反而已,如果把序列X看作神经网络输入,W看做神经网络对序列X进行线性组合的权重序列;而对于神经网络来说,只要权重序列中的权重是可以学习的,那么它的顺序就无关紧要,互相关运算和卷积运算就没有本质区别;
在图神经网络中,输入一般不是一维的,更多是高维的,用的是更高维的互相关和卷积,对于二维的互相关计算原理,后续会慢慢更新;