提起卷积运算相信大家都不陌生，这是一种很常见的运算。我们在学习《信号与系统》时就一直在和卷积打交道，在后来的一些课程中也有卷积运算的身影，比如《自动控制原理现代部分》中的卷积定理等。
在学习《信号与系统》时我们知道了卷积的定义，对于两个函数$f(x)$和 $g(x)$，他们的卷积 $f\ast g(n)$ 的公式如下：
连续形式：$\mathrm{f}\ast \mathrm{g}(n)={\int }_{-\infty }^{+\infty }f(\tau )\ast g(n-\tau )d\tau$ //n为实数
离散形式：$\mathrm{f}\ast \mathrm{g}(n)={\sum }_{\tau =-\infty }^{+\infty }f(\tau )\ast g(n-\tau )//\mathrm{n},\tau$为正整数
通过如上公式可以看到，卷积其实就是将一个函数 先进行翻转（公式中体现为$-\tau$或$-n$）再向右平移$n$或$N$的长度后得到函数$g^{\ast }$,再让$g^{\ast }$和$f$进行累积求和或相乘求积分。通过分析我们已经知道了卷积的运算方法，也知道了卷积计算名字的由来：‘卷’就是对 进行的翻转和平移过程，就像卷纸巾一样，‘积’就是积求和或相乘求积分的过程。

我们对于卷积的理解一般就是这样了。但是卷积运算的意义究竟是什么呢？对于函数$g(x)$为什么要进行翻转后在平移的操作呢？平移的长度$n$代表着什么意义呢？带着这样的问题，我在网络上查阅了一些资料，最终写出一些体会与大家分享，来回答这三个问题。
一：卷积运算的意义是什么？
我们先抛开运算过程中对$g$所作的翻转和平移过程，设$g$作了翻转和平移得到函数 $g^{\ast }$，$g^{\ast }$与 $f$所做的运算其实可以理解为 函数在 函数上的加权叠加。从信号的角度上来讲，也就是说将$f$函数（$f$ 一般在信号中是指输入信号，$g$在信号中一般指响应函数）上各个选定的时间点上按照$g\ast$所规定的权值进行加权叠加。如下图所示，假设$g(n)$未知，$g^{\ast }(n)=e^n$，为一个衰减函数，则对应相乘累加后的卷积：$$\begin{array}{l}f\ast g(n)=f(0)+f(1)\ast e^{-1}+f(2)\ast e^{-2}+f(3)\ast e^{-3}+\\ f(4)\ast e^{-4}+f(5)\ast e^{-5}+f(6)\ast e^{-6}+f(7)\ast e^{-7}+f(8)\ast \\ e^{-8}+f(9)\ast e^{-9}+f(10)\ast e^{-10}+\cdots +f(n)\ast e^{-n}\end{array}$$公式中的结果就是$f$信号各时间点采集值的加权和。

二：为什么要对$g$进行翻转后在平移的操作及平移的长度$n$代表着什么意义？
沿用上一个问题中的举例，首先输入信号$f$离散后的图像如下图的红色轨迹，对于这个输入信号，$f(0)$表示$t=0$时刻的信号，$f(1)$表示$t=1$时刻的信号，。。。$f(10)$表示$t=10$时刻的信号，也是图中最后进入的信号，也就是最新的信号。而途中的响应函数$g$离散后如下图的黑色轨迹，是一个指数衰减函数，其物理意义是信号经过响应函数后随着时间的流逝会不断衰减，如$t=0$时输入信号$f(0)$在$t=1$时刻衰减为$f(0)\ast e^{-1}$ ,在$t=3$时刻衰减为$f(0)\ast e^{-3}$ ,$t=1$时刻的信号在$t=2$时刻时衰减为$f(1)\ast e^{-1}$，最终在$t=n$的时刻求得所有采集到的输入信号经过时间衰减后的输出和$F(n)$。这个输出$F(n)$的值受到在$t=0$时刻到$t=n$时刻之间所有采集到的输入信号的影响，只是随着时间的流逝，越早采集的信号对当前的输出影响就越小。

因此，输入信号f通过与g函数进行某种运算后可以得到输出$F(n)$ 。而这之间的运算关系是怎样的呢？通过上述分析我们假设要求取$F(5)$，即$t=5$时刻及之前所有采集到的信号的一个加权求和。按照分析:$$\begin{array}{l}F(5)=\\ f(0)\ast e^{-5}+f(1)\ast e^{-4}+f(2)\ast e^{-3}+f(3)\ast e^{-2}+f(4)\ast e^{-1}+f(5)\end{array}$$因为$f(0)$是最早采集到的信号，故其衰减的最为厉害，权值也最小。将其中的权值用响应函数$g$来表示，则$$\begin{array}{l}F(5)=\\ f(0)\ast g(5)+f(1)\ast g(4)+f(2)\ast g(3)+f(3)\ast g(2)+f(4)\ast g(1)+f(5)\ast g(0)\\ =\\ f(0)\ast g(5-0)+f(1)\ast g(5-1)+f(2)\ast g(5-2)+f(3)\ast g(5-3)+f(4)\ast g(5-4)+f(5)\ast g(5-5)\\ =\\ {\sum }_{\tau =0}^{5}f(\tau )\ast g(5-\tau )\end{array}$$看到这个公式大家有没有一点熟悉的感觉，没错这个式子$F(5)=su{m}_{\tau =0}^{5}f(\tau )\ast g(5-\tau )$和卷积运算的离散形式${\sum }_{\tau =-\infty }^{+\infty }f(\tau )\ast g(n-\tau )$几乎一模一样，只是把$n$取了整数5。
看到这里可能大家已经隐约知道了卷积运算中对g进行翻转和平移的作用，为了让大家更直观的看到翻转和平移作用，引用知乎博主palet的解释:

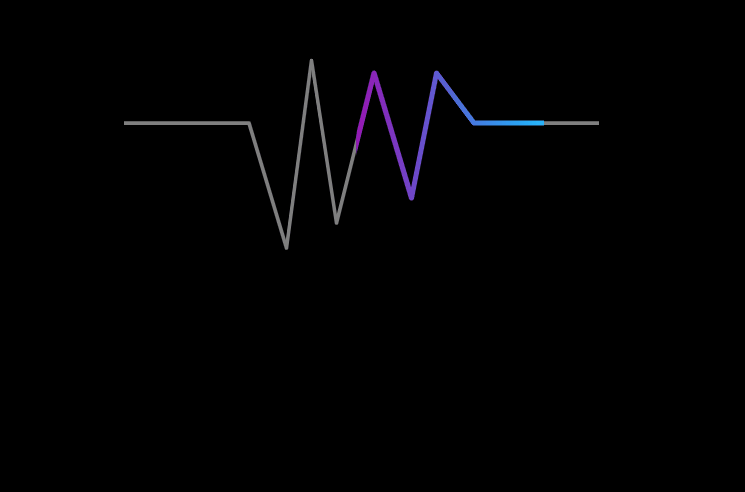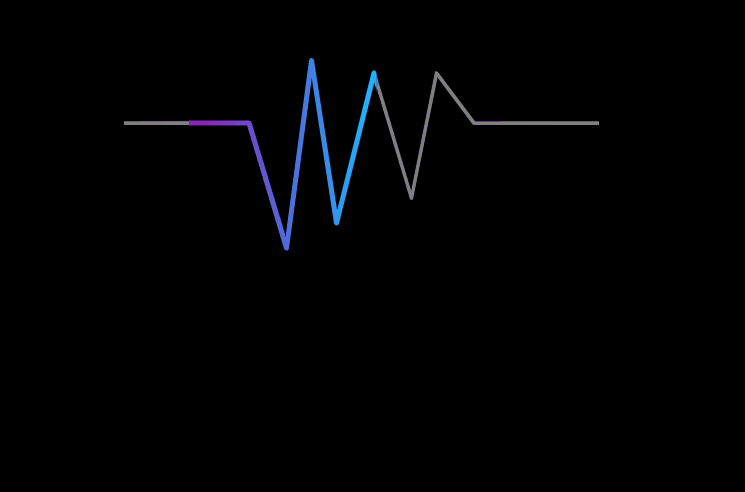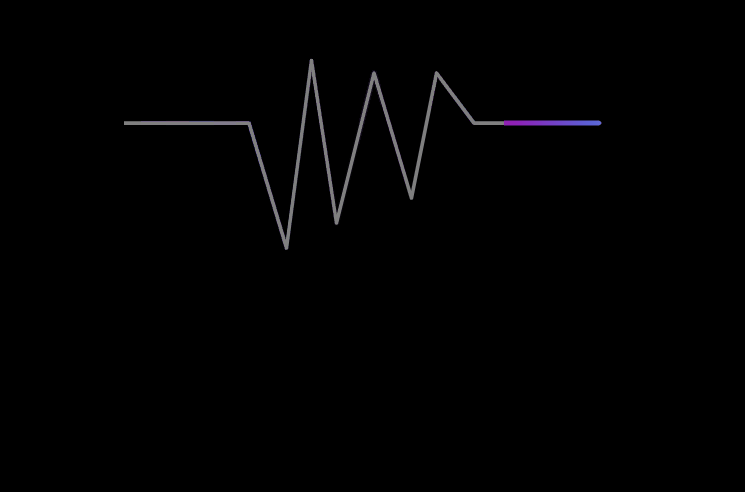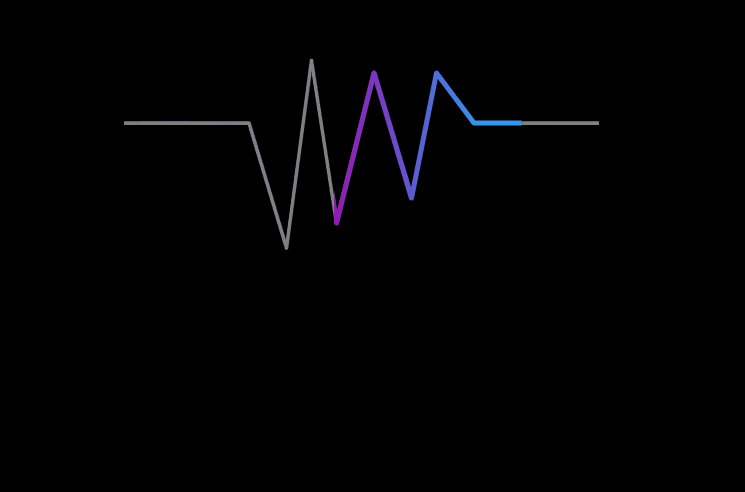
首先这是给定的输入信号$f$和指数衰减响应函数$g$ 。为了达到上文提到的加权求和的效果，当取T（也就是上文的$n$）=10时，$f(t)$和$g(t)$的累积对应关系如下图所示：

如上图所示，对于$t=10$时刻最新的信号采集值$f(10)$是完全没有衰减的，因此与$g(0)=1$相乘，对于其它时刻的对应也如上分析，最终得到最近10个输入信号的采集值加权叠加的结果，具体请参看第二个问题的第二段。
这样的对应关系看起来十分复杂，因此我们对$g(t)$进行一些处理，首先进行翻转，翻转后$f(t)$与$g(-t) $的乘积对应关系如下图：

翻转之后乘积的对应关系似乎看起了有了一些规则，但依旧有些不易观察，之后对$g(-t)$进行长度为T（上文的$n$）的右移得到$g(T-t)$，其对应关系变为了下图：

通过这张图后可以很清晰的看见$f(t)$与$g(T-t)$的乘积对应关系。又因为$f(t)$是实际的输入信号，其在$t$的负半轴是没有数值的，因此$f(t)$与$g(t)$做卷积运算也就是$f(t)$与$g(T-t)$做整个数轴上的累积运算时与作$(0,T)$的累积运算结果是相同的。因此可以得出卷积运算满足了信号指数衰减求和的结果。大家应该也明白了卷积运算在信号处理上的物理意义。同时大家也能够明白了平移长度$n$所代表的意义了，$n$代表的就是积分的x轴长度或者累加的次数，在信号上就是当前已采集输入信号值的次数。
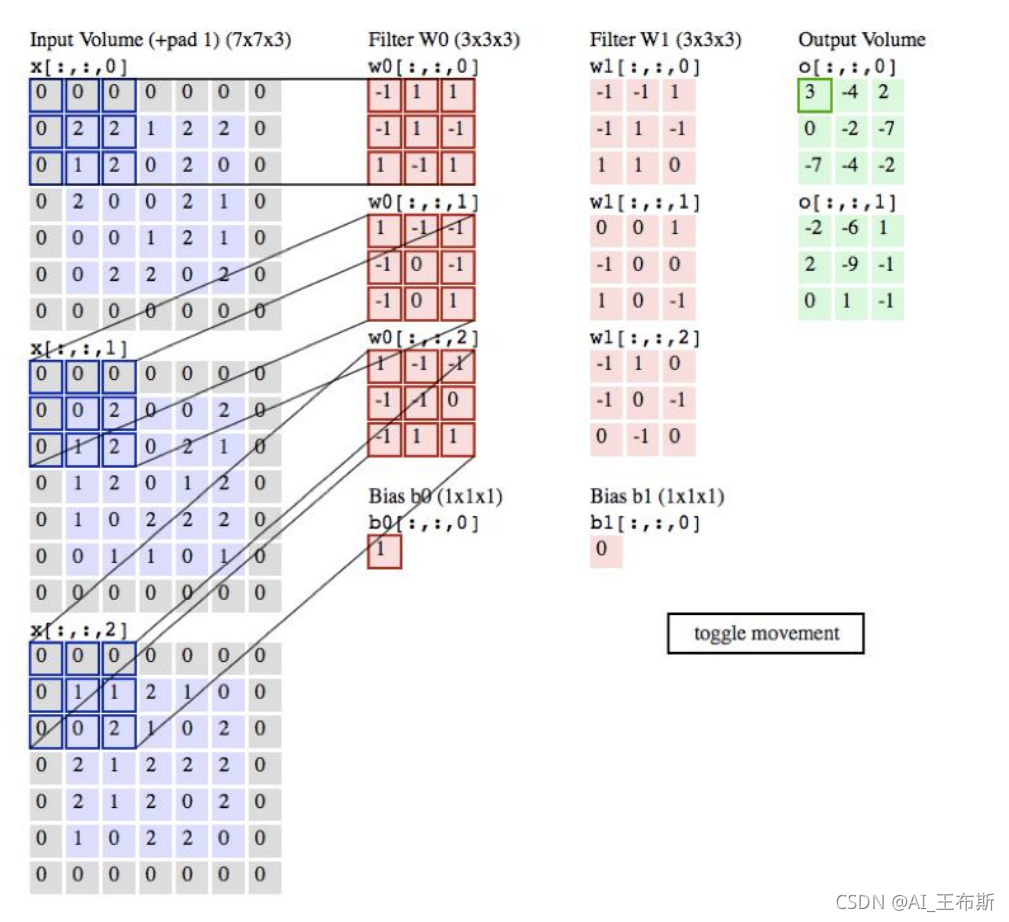
本文主要分享的是卷积运算在信号处理上的一些物理意义，希望能够帮助读者更好的理解卷积运算。但实际上卷积运算在很多其他的地方也有很大的作用，比如图像识别中的边缘提取，卷积神经网络等等，有兴趣的话大家可以自行去了解。