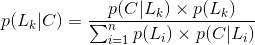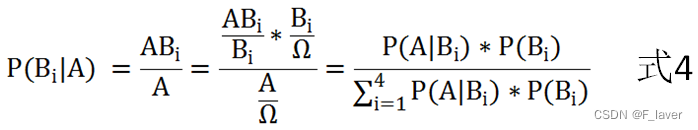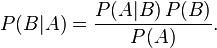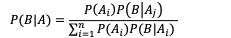贝叶斯法则（公式）

article/2025/9/24 10:25:32

转自：MBA智库侵权删

文章目录

- - - 概念
    - 贝叶斯法则（公式）原理
    - 贝叶斯法则实例

概念

什么是贝叶斯法则
　　贝叶斯的统计学中有一个基本的工具叫贝叶斯法则、也称为贝叶斯公式，尽管它是一个数学公式，但其原理毋需数字也可明了。如果你看到一个人总是做一些好事，则那个人多半会是一个好人。这就是说，当你不能准确知悉一个事物的本质时，你可以依靠与事物特定本质相关的事件出现的多少去判断其本质属性的概率。用数学语言表达就是：支持某项属性的事件发生得愈多，则该属性成立的可能性就愈大。

贝叶斯法则又被称为贝叶斯定理、贝叶斯规则是概率统计中的应用所观察到的现象对有关概率分布的主观判断（即先验概率）进行修正的标准方法。

所谓贝叶斯法则，是指当分析样本大到接近总体数时，样本中事件发生的概率将接近于总体中事件发生的概率。

但行为经济学家发现，人们在决策过程中往往并不遵循贝叶斯规律，而是给予最近发生的事件和最新的经验以更多的权值，在决策和做出判断时过分看重近期的事件。面对复杂而笼统的问题，人们往往走捷径，依据可能性而非根据概率来决策。这种对经典模型的系统性偏离称为“偏差”。由于心理偏差的存在，投资者在决策判断时并非绝对理性，会行为偏差，进而影响资本市场上价格的变动。但长期以来，由于缺乏有力的替代工具，经济学家不得不在分析中坚持贝叶斯法则。
　通常，事件A在事件B(发生)的条件下的概率，与事件B在事件A的条件下的概率是不一样的；然而，这两者是有确定的关系,贝叶斯法则就是这种关系的陈述。

贝叶斯法则（公式）原理

作为一个规范的原理，贝叶斯法则对于所有概率的解释是有效的；然而，频率主义者和贝叶斯主义者对于在应用中概率如何被赋值有着不同的看法：频率主义者根据随机事件发生的频率，或者总体样本里面的个数来赋值概率；贝叶斯主义者要根据未知的命题来赋值概率。一个结果就是，贝叶斯主义者有更多的机会使用贝叶斯法则。

贝叶斯法则是关于随机事件A和B的条件概率和边缘概率的。

$\Pr(A|B) = \frac{\Pr(B | A), \Pr(A)}{\Pr(B)}\propto L(A | B), \Pr(A) !$

其中L(A|B)是在B发生的情况下A发生的可能性。

在贝叶斯法则中，每个名词都有约定俗成的名称：

Pr(A)是A的先验概率或边缘概率。之所以称为"先验"是因为它不考虑任何B方面的因素。
Pr(A|B)是已知B发生后A的条件概率，也由于得自B的取值而被称作A的后验概率。
Pr(B|A)是已知A发生后B的条件概率，也由于得自A的取值而被称作B的后验概率。
Pr(B)是B的先验概率或边缘概率，也作标准化常量（normalized constant）。
　　按这些术语，Bayes法则可表述为：

后验概率 = (相似度 * 先验概率)/标准化常量
　　也就是说，后验概率与先验概率和相似度的乘积成正比。

另外，比例Pr(B|A)/Pr(B)也有时被称作标准相似度（standardised likelihood），Bayes法则可表述为：

后验概率 = 标准相似度 * 先验概率

贝叶斯法则实例

可以将贝叶斯法则的分析思路表达如下。

挑战者B不知道原垄断者A是属于高阻挠成本类型还是低阻挠成本类型，但B知道，如果A属于高阻挠成本类型，B进入市场时A进行阻挠的概率是20%（此时A为了保持垄断带来的高利润，不计成本地拼命阻挠）；如果A属于低阻挠成本类型，B进入市场时A进行阻挠的概率是100%。

博弈开始时，B认为A属于高阻挠成本企业的概率为70%，因此，B估计自己在进入市场时，受到A阻挠的概率为：

0.7×0.2+0.3×1=0.44

0.44是在B给定A所属类型的先验概率下，A可能采取阻挠行为的概率。

当B进入市场时，A确实进行阻挠。使用贝叶斯法则，根据阻挠这一可以观察到的行为，B认为A属于高阻挠成本企业的概率变成A属于高成本企业的概率=0.7（A属于高成本企业的先验概率）×0.2（高成本企业对新进入市场的企业进行阻挠的概率）÷0.44=0.32

根据这一新的概率，B估计自己在进入市场时，受到A阻挠的概率为：

0.32×0.2+0.68×1=0.744

如果B再一次进入市场时，A又进行了阻挠。使用贝叶斯法则，根据再次阻挠这一可观察到的行为，B认为A属于高阻挠成本企业的概率变成

A属于高成本企业的概率=0.32（A属于高成本企业的先验概率）×0.2（高成本企业对新进入市场的企业进行阻挠的概率）÷0.744=0.086

这样，根据A一次又一次的阻挠行为，B对A所属类型的判断逐步发生变化，越来越倾向于将A判断为低阻挠成本企业了。

以上例子表明，在不完全信息动态博弈中，参与人所采取的行为具有传递信息的作用。尽管A企业有可能是高成本企业，但A企业连续进行的市场进入阻挠，给B企业以A企业是低阻挠成本企业的印象，从而使得B企业停止了进入地市场的行动。

应该指出的是，传递信息的行为是需要成本的。假如这种行为没有成本，谁都可以效仿，那么，这种行为就达不到传递信息的目的。只有在行为需要相当大的成本，因而别人不敢轻易效仿时，这种行为才能起到传递信息的作用。

传递信息所支付的成本是由信息的不完全性造成的。但不能因此就说不完全信息就一定是坏事。研究表明，在重复次数有限的囚徒困境博弈中，不完全信息可以导致博弈双方的合作。理由是：当信息不完全时，参与人为了获得合作带来的长期利益，不愿过早暴露自己的本性。这就是说，在一种长期的关系中，一个人干好事还是干坏事，常常不取决于他的本性是好是坏，而在很大程度上取决于其他人在多大程度上认为他是好人。如果其他人不知道自己的真实面目，一个坏人也会为了掩盖自己而在相当长的时期内做好事。