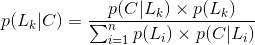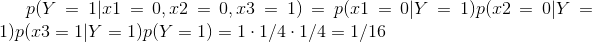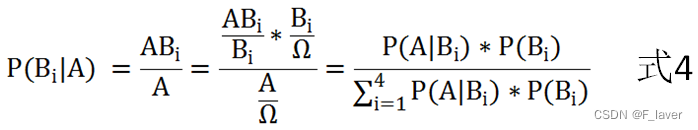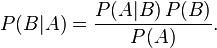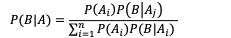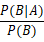简介

贝叶斯定理是18世纪英国数学家托马斯·贝叶斯（Thomas Bayes）提出得重要概率论理论。以下摘一段 wikipedia 上的简介：

所谓的贝叶斯定理源于他生前为解决一个“逆概”问题写的一篇文章，而这篇文章是在他死后才由他的一位朋友发表出
来的。在贝叶斯写这篇文章之前，人们已经能够计算“正向概率”，如“假设袋子里面有 N 个白球，M 个黑球，你伸手
进去摸一把，摸出黑球的概率是多大”。而一个自然而然的问题是反过来：“如果我们事先并不知道袋子里面黑白球
的比例，而是闭着眼睛摸出一个（或好几个）球，观察这些取出来的球的颜色之后，那么我们可以就此对袋子里
面的黑白球的比例作出什么样的推测”。这个问题，就是所谓的逆向概率问题。

概率复习

在正式介绍公式前，先通过几道简单的概率题来复习概率相关的知识

职业	体型	女神是否喜欢
程序员	超重	不喜欢
产品	匀称	喜欢
程序员	匀称	喜欢
程序员	超重	喜欢
美工	匀称	不喜欢
美工	超重	不喜欢
产品	匀称	喜欢

1.女神喜欢的概率?
2.职业是程序员并且体型匀称的概率?
3.在女神喜欢的条件下，职业是程序员的概率?
4.在女神喜欢的条件下，职业是产品，体重是超重的概率?

在解答前先引入几个概念
事件A发生的概率记作P(A)
联合概率：事件A与事件B同时成立的概率
记作：P(A,B)=P(A)P(B)
条件概率：事件A在另一个事件B已经发生条件下的成立概率
记作：P(A|B)
特性:P(A1,A2|B)=P(A1|B)P(A2|B)

代入公式分别为
1.P(女神喜欢)
2.P(程序员,体型匀称)
3.P(程序员|女神喜欢)
4.P(产品，超重|女神喜欢)

公式定义

贝叶斯定理是关于随机事件 A 和 B 的条件概率：

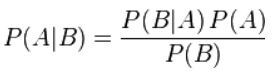
先根据上面的例子核对公式
3.P(程序员|女神喜欢)=P(女神喜欢|程序员)P(程序员)/P(女神喜欢)=?
2/3*3/7 / 4/7

其中P(A|B)是在 B 发生的情况下 A 发生的可能性。
在贝叶斯定理中，每个名词都有约定俗成的名称：

P(A)是 A 的先验概率，之所以称为“先验”是因为它不考虑任何 B 方面的因素。
P(A|B)是已知 B 发生后 A 的条件概率，也由于得自 B 的取值而被称作 A 的后验概率。
P(B|A)是已知 A 发生后 B 的条件概率，也由于得自 A 的取值而被称作 B 的后验概率。
P(B)是 B 的先验概率，也作标淮化常量（normalizing constant）。

按这些术语，贝叶斯定理可表述为：
后验概率 = (相似度 * 先验概率)/标淮化常量
也就是说，后验概率与先验概率和相似度的乘积成正比。
另外，比例P(B|A)/P(B)也有时被称作标淮相似度（standardised likelihood），Bayes定理可表述为：
后验概率 = 标淮相似度 * 先验概率
条件概率就是事件 A 在另外一个事件 B 已经发生条件下的发生概率。条件概率表示为P(A|B)，
读作“在 B 发生的条件下 A 发生的概率”。

联合概率表示两个事件共同发生（数学概念上的交集）的概率。A 与 B 的联合概率表示为

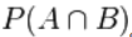
推导

我们可以从条件概率的定义推导出贝叶斯定理。

根据条件概率的定义，在事件 B 发生的条件下事件 A 发生的概率为：

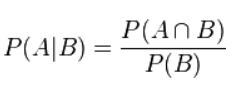
同样地，在事件 A 发生的条件下事件 B 发生的概率为：

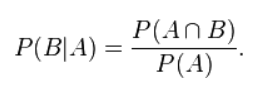
结合这两个方程式，我们可以得到：

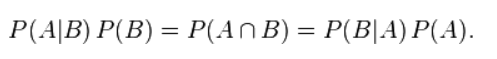
这个引理有时称作概率乘法规则。上式两边同除以 P(A)，若P(A)是非零的，我们可以得到贝叶斯定理:

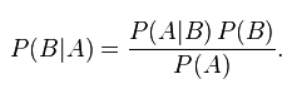
实际应用

问题替换
P(科技|文档)=P(科技|词1，词2，词3)=P(词1，词2，词3|科技)*P(科技) / P(词1，词2，词3)
P(水果税收编码|商品名称)=P(水果税收编码|词1，词2，词3)

现有一篇被预测文档：出现了影院，支付宝，云计算，计算属于科技、娱乐的类别概率？

思考：属于某个类别为0，合适吗？

根据名称判断男女

所需要训练集下载地址
http://sofasofa.io/competition.php?id=3#c1

import pandas as pd
from collections import defaultdict
import math# 处理名称中的空格和特殊字符
def handleName(name):name.strip()name = ''.join(name.split())name.replace(' ', '')name = name[1:]first = name.find("（")last = name.find("）")if first != -1 and last != -1:name = name[0:first]return nametest = pd.read_csv("name.csv")
test['chuLiNmae'] = test['name'].apply(handleName)# 读取train.txt
train = pd.read_csv('train.txt')# 把数据分为男女两部分
names_female = train[train['gender'] == 0]
names_male = train[train['gender'] == 1]# 统计男女的人数
totals = {'f': len(names_female),'m': len(names_male)}# 女性词汇累积发生概率
frequency_list_f = defaultdict(int)
for name in names_female['name']:for char in name:frequency_list_f[char] += 1. / totals['f']# 男性词汇累积发生概率
frequency_list_m = defaultdict(int)
for name in names_male['name']:for char in name:frequency_list_m[char] += 1. / totals['m']# 计算时增加默认拉普拉斯平滑系数alpha
def LaplaceSmooth(char, frequency_list, total, alpha=1.0):count = frequency_list[char] * totaldistinct_chars = len(frequency_list)freq_smooth = (count + alpha) / (total + distinct_chars * alpha)return freq_smooth# 运用贝叶斯公式计算其某种性别的概率
def GetLogProb(char, frequency_list, total):freq_smooth = LaplaceSmooth(char, frequency_list, total)return math.log(freq_smooth) - math.log(1 - freq_smooth)# 累积每个词汇对应性别的概率
def ComputeLogProb(name, bases, totals, frequency_list_m, frequency_list_f):logprob_m = bases['m']logprob_f = bases['f']for char in name:logprob_m += GetLogProb(char, frequency_list_m, totals['m'])logprob_f += GetLogProb(char, frequency_list_f, totals['f'])return {'male': logprob_m, 'female': logprob_f}# 得到最终答案
def GetGender(LogProbs):return LogProbs['male'] > LogProbs['female']# 求女生的概率的自然对数
base_f = math.log(1 - train['gender'].mean())
# 求女生所有词汇发生概率之和
base_f += sum([math.log(1 - frequency_list_f[char]) for char in frequency_list_f])# 求男的概率的自然对数
base_m = math.log(train['gender'].mean())
# 求男生所有词汇发生概率之和
base_m += sum([math.log(1 - frequency_list_m[char]) for char in frequency_list_m])# 得到男女所有词汇发生的概率值的自然对数
bases = {'f': base_f, 'm': base_m}
result = []
for name in test['chuLiNmae']:# 得到一个名字准备预测性别LogProbs = ComputeLogProb(name, bases, totals, frequency_list_m, frequency_list_f)gender = GetGender(LogProbs)result.append(int(gender))test['gender'] = resulttest.to_csv('MyXingBie.csv', index=False)

最终结果

一平,1
昶胜,1
馨,0
星驰,1
梦媛,0
陈,1
忠良,1
浪,1
建,1
小惠,0