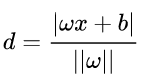模式识别中的最优分类超平面与线性支持向量机

---

本章的内容需要你理解一下的基础知识。

模式识别部分：线性分类器基本概念、感知器

数学基础部分：拉格朗日乘子法、拉格朗日对偶问题

当然，以上的基础知识不需要你现在就看，可以在阅读中需要时去看。以上只是提醒你需要了解这些内容。

---

在线性可分的情况下，我们讨论了感知器的用法，可以发现在解区间有无限多的解向量。在感知器方法中，我们用梯度下降法求解一个解向量。不同的初始值和迭代参数就会得到不同的解。但肯定会有一个最好的解呀！

最优分类超平面

我们考虑只有两类情况下定义训练样本集为
( x 1 ⃗ , y 1 ) , ( x 2 ⃗ , y 2 ) , … , ( x N ⃗ , y N ) , x i ⃗ ∈ R d , y i ∈ { + 1 , − 1 } (1) (\vec{x_1},y_1),(\vec{x_2},y_2),\dots,(\vec{x_N},y_N),~~~~\vec{x_i}\in R^d ,y_i\in \{+1,-1\}\tag{1} (x1​ ​,y1​),(x2​ ​,y2​),…,(xN​ ​,yN​),    xi​ ​∈Rd,yi​∈{+1,−1}(1)
其中样本$\overrightarrow{x_i}$有$d$个特征（$d$维向量），$y_i$则是类别标号，当样本属于第一类时$y_i=+1$，样本属于第二类时$y_i=-1$。那么存在一个超平面
$$g(\vec{x})=(\vec{\mathbf{w}}\vec{x}+b)=0\text{\hspace{1em}(2)}$$
是不是决定这个式子很奇怪？与我们之前学的判别函数$g(\vec{x})={\vec{\mathbf{w}}}^T\vec{x}+w_0$很像呢？式（2）是许多支持向量机的写法，书中也采用式（2）这种写法，那我们也这样写吧。

现在强调一下最优分类面的定义：一个超平面，如果它能够将训练样本没有错误地分开，并且两类训练样本中离超平面最近的样本与超平面之间的距离是最大的。图一中，分为蓝绿两类，我们假设红色直线就是最优分类超平面，那么它能将训练样本没有错误地分开，同时样本$\overrightarrow{x_1}$和$\overrightarrow{x_2}$离该超平面的距离最近且距离最大。

我们定义最优超平面的分类决策函数为
$$f(\vec{x})=sgn(g(\vec{x}))=sgn(\vec{\mathbf{w}}\vec{x}+b)\text{\hspace{1em}(3)}$$
其中$sgn()$为符号函数，当自变量为正值时取值为1,否则为-1 。

我们在线性分类基础中可以知道，权向量$\vec{\mathbf{w}}$的方向决定了超平面的方向，而其大小$||\vec{\mathbf{w}}||$只能求解向量$\vec{x}$到分类面$g(\vec{x})=0$的距离是$\frac{|g(\vec{x})|}{||\vec{\mathbf{w}}||}$。$b$的作用就是对超平面$g(\vec{x})=0$的一个偏移。既然我们知道了最优分类面的定义，那么就可以写出如下公式：
$$\{\begin{array}{cc}(\vec{\mathbf{w}}\overrightarrow{x_i}+b)\ge 1,& y_i=+1\\ (\vec{\mathbf{w}}\overrightarrow{x_i}+b)\le -1,& y_i=-1\end{array}\text{\hspace{1em}(4)}$$
我们看第一行要求第一类样本中$g(\vec{x})$最小等于1，这个1指的是单位距离，实际的距离是$\frac{1}{||\vec{\mathbf{w}}||}$，代表的是两类训练样本中离超平面最近的样本与超平面之间的距离是一样大小的。那么我们求解式（4）的目的便是让这个距离最大！式（4）中两个式子看起来是不是很相似，我们可以想办法将他们合并到一个式子中：
$$y_i(\vec{\mathbf{w}}\overrightarrow{x_i}+b)\ge 1,i=1,2,...,N\text{\hspace{1em}(5)}$$
如何让两类训练样本中离超平面最近的样本与超平面之间的距离最大呢？我们在式（4）确定了两个边界，分别是$g(\vec{x})=1$和$g(\vec{x})=-1$他们到$g(\vec{x})=0$的距离分别都是$\frac{1}{||\vec{\mathbf{w}}||}$。那么分类间隔就是$M=\frac{2}{||\vec{\mathbf{w}}||}$。为了在计算中方便，我们给$M$任意的进行变化但保持单调性不便，并不会改变最终的结果。于是，求解最优超平面的问题就变成了：
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||\vec{\mathbf{w}}|{|}^2 \\ s.t.y_i(\vec{\mathbf{w}}\overrightarrow{x_i}+b)\ge 1,i=1,2,...,N\text{\hspace{1em}(6)} \end{gathered}$$

看到这熟悉的约束条件形式，我们知道肯定要使用拉格朗日乘子法。对每一个样本引入一个朗格朗日系数
$$a_i\ge 0,i=1,2,...,N\text{\hspace{1em}(7)}$$
我们可以把式（6）转化为拉格朗日函数
L = 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 + ∑ i = 1 N α i { 1 − [ y i ( w ⃗ x i ⃗ + b ) ] } (8) L=\frac{1}{2}||\mathbf{\vec{w}}||^2+\sum^N_{i=1}\alpha_i \{1-[y_i(\mathbf{\vec{w}}\vec{x_i}+b)]\}\tag{8} L=21​∣∣w ∣∣2+i=1∑N​αi​{1−[yi​(w xi​ ​+b)]}(8)
式（11）是对一组公式的方便记忆，实际上求解的方程有：
{ ∂ L ∂ w ⃗ = 0 ∂ L ∂ b = 0 α i ≥ 0 1 − [ y i ( w ⃗ x i ⃗ + b ) ] ≤ 0 α i { 1 − [ y i ( w ⃗ x i ⃗ + b ) ] } = 0 （ K K T 条件） (9) \left\{\begin{matrix} \frac{\partial L}{\partial \mathbf{\vec{w}}}=0\\ \frac{\partial L}{\partial b}=0\\ \alpha_i \ge 0\\ 1-[y_i(\mathbf{\vec{w}}\vec{x_i}+b)]\le0\\ \alpha_i \{1-[y_i(\mathbf{\vec{w}}\vec{x_i}+b)]\}=0~（KKT条件） \end{matrix}\right.\tag{9} ⎩ ⎨ ⎧​∂w ∂L​=0∂b∂L​=0αi​≥01−[yi​(w xi​ ​+b)]≤0αi​{1−[yi​(w xi​ ​+b)]}=0 （KKT条件）​(9)

$$\frac{\partial L}{\partial \vec{\mathbf{w}}}=\vec{\mathbf{w}}-\sum _{i=1}^N{\alpha }_i{y}_i\overrightarrow{x_i}=0\Rightarrow {\vec{\mathbf{w}}}^{\ast }=\sum _{i=1}^N{\alpha }_i{y}_i\overrightarrow{x_i}\text{\hspace{1em}(10)}$$

同理可以计算$\frac{\partial L}{\partial b}=0$得到
$$\sum _{i=1}^N{\alpha }_i{y}_i=0\text{\hspace{1em}(11)}$$

其实由式（10）和式（11）我们就可以暴力求解得到决策方程式（3）了，但是这样暴力求解很复杂，将要求解的未知数有：$\vec{\mathbf{w}},b,{\alpha }_1,...,{\alpha }_N$，值得注意的是未知量$\vec{\mathbf{w}}$是一个向量，其中包含的未知数${\mathbf{w}}_k$与维数有关。这是非常难以求解的。那么我们可以将它转化为对偶问题，使得求解更加简单。

利用拉格朗日对偶问题求解最优超平面

---

下面是转化为对偶问题的推倒过程。

转为对偶问题

为了使分类间隔尽可能大，我们就是要求解下面的条件极值
$$\begin{gathered} \underset{w,b}{\min }\frac{1}{2}||\vec{\mathbf{w}}|{|}^2 \\ s.t.y_i(\vec{\mathbf{w}}\overrightarrow{x_i}+b)\ge 1,i=1,2,...,N\text{\hspace{1em}(12)} \end{gathered}$$
由式（12）写出拉格朗日函数为：
L = 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 + ∑ i = 1 N α i { 1 − [ y i ( w ⃗ x i ⃗ + b ) ] } (13) L=\frac{1}{2}||\mathbf{\vec{w}}||^2+\sum^N_{i=1}\alpha_i \{1-[y_i(\mathbf{\vec{w}}\vec{x_i}+b)]\}\tag{13} L=21​∣∣w ∣∣2+i=1∑N​αi​{1−[yi​(w xi​ ​+b)]}(13)
我们可以尝试求解$\underset{\lambda }{\max }L$会得到什么：
max ⁡ α L = max ⁡ α 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 + ∑ i = 1 N α i { 1 − [ y i ( w ⃗ x i ⃗ + b ) ] } (14) \underset{\alpha}{\max}L =\underset{\alpha}{\max}\frac{1}{2}||\mathbf{\vec{w}}||^2 +\sum^N_{i=1}\alpha_i \{1-[y_i(\mathbf{\vec{w}}\vec{x_i}+b)]\}\tag{14} αmax​L=αmax​21​∣∣w ∣∣2+i=1∑N​αi​{1−[yi​(w xi​ ​+b)]}(14)
式（14）中，由式（9）知 ∑ i = 1 N α i { 1 − [ y i ( w ⃗ x i ⃗ + b ) ] } ≤ 0 \sum^N_{i=1}\alpha_i \{1-[y_i(\mathbf{\vec{w}}\vec{x_i}+b)]\}\le0 ∑i=1N​αi​{1−[yi​(w xi​ ​+b)]}≤0，那么
$$\frac{1}{2}||\vec{\mathbf{w}}|{|}^2=\underset{\alpha }{\max }L\text{\hspace{1em}(15)}$$
将式（15）代入到式（12）中，可以将原问题改写为：
$$\begin{gathered} \underset{\vec{\mathbf{w}},b}{\min }\underset{\alpha }{\max }L \\ s.t.{\alpha }_i\ge 0\text{\hspace{1em}(16)} \end{gathered}$$
根据拉格朗日对偶性（证明可以看文章开头的链接），进一步改写为：
$$\begin{gathered} \underset{\alpha }{\max }\underset{\vec{\mathbf{w}},b}{\min }L \\ s.t.{\alpha }_i\ge 0\text{\hspace{1em}(17)} \end{gathered}$$
式（17）就是对偶问题。对偶问题和原问题同解，而且更方便求解。

求解对偶问题中的$\underset{\vec{\mathbf{w}},b}{\min }L$

我们在之前已经得到了
$${\vec{\mathbf{w}}}^{\ast }=\sum _{i=1}^N{\alpha }_i{y}_i\overrightarrow{x_i}\text{\hspace{1em}(18)}$$

$$\sum _{i=1}^N{\alpha }_i{y}_i=0\text{\hspace{1em}(19)}$$

将式（18）和式（19）代入$L$就是得到了$\underset{\vec{\mathbf{w}},b}{\min }L$:
min ⁡ w ⃗ , b L = 1 2 ∣ ∣ w ⃗ ∣ ∣ 2 + ∑ i = 1 N α i { 1 − [ y i ( w ⃗ x i ⃗ + b ) ] } = 1 2 w ⃗ T w ⃗ + ∑ i = 1 N α i − ∑ i = 1 N α i y i ( w ⃗ T x i ⃗ ) + ∑ i = 1 n α i y i b = 1 2 ∑ i = 1 N α i y i x i ⃗ T ∑ j = 1 N α j y j x j ⃗ + ∑ i = 1 N α i − ∑ i = 1 N α i y i x i ⃗ T ∑ j = 1 N α j y j x j ⃗ + 0 = ∑ i = 1 N α i − 1 2 ∑ i = 1 N ∑ j = 1 N α i y i α j y j x i ⃗ T x j ⃗ (20) \underset{\mathbf{\vec{w}},b}{\min}L=\frac{1}{2}||\mathbf{\vec{w}}||^2+\sum^N_{i=1}\alpha_i \{1-[y_i(\mathbf{\vec{w}}\vec{x_i}+b)]\}\\ =\frac{1}{2}\mathbf{\vec{w}}^T\mathbf{\vec{w}}+\sum^N_{i=1}\alpha_i-\sum^N_{i=1}\alpha_iy_i(\mathbf{\vec{w}}^T\vec{x_i})+\sum^n_{i=1}\alpha_iy_ib\\ =\frac{1}{2}\sum^N_{i=1}\alpha_iy_i\vec{x_i}^T\sum^N_{j=1}\alpha_jy_j\vec{x_j}+\sum^N_{i=1}\alpha_i-\sum^N_{i=1}\alpha_iy_i\vec{x_i}^T\sum^N_{j=1}\alpha_jy_j\vec{x_j}+0\\ =\sum^N_{i=1}\alpha_i-\frac{1}{2}\sum^N_{i=1}\sum^N_{j=1}\alpha_iy_i\alpha_jy_j\vec{x_i}^T\vec{x_j}\tag{20} w ,bmin​L=21​∣∣w ∣∣2+i=1∑N​αi​{1−[yi​(w xi​ ​+b)]}=21​w Tw +i=1∑N​αi​−i=1∑N​αi​yi​(w Txi​ ​)+i=1∑n​αi​yi​b=21​i=1∑N​αi​yi​xi​ ​Tj=1∑N​αj​yj​xj​ ​+i=1∑N​αi​−i=1∑N​αi​yi​xi​ ​Tj=1∑N​αj​yj​xj​ ​+0=i=1∑N​αi​−21​i=1∑N​j=1∑N​αi​yi​αj​yj​xi​ ​Txj​ ​(20)
所以对偶问题可以写为：
$$\begin{gathered} \underset{\alpha }{\max }\sum _{i=1}^N{\alpha }_i-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{y}_i{\alpha }_j{y}_j{\overrightarrow{x_i}}^T\overrightarrow{x_j} \\ s.t.{\alpha }_i\ge 0,\sum _{i=1}^N{\alpha }_i{y}_i=0\text{\hspace{1em}(21)} \end{gathered}$$
但习惯上修改为求最小值（与书本不同）：
$$\begin{gathered} \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{y}_i{\alpha }_j{y}_j{\overrightarrow{x_i}}^T\overrightarrow{x_j}-\sum _{i=1}^N{\alpha }_i \\ s.t.{\alpha }_i\ge 0,\sum _{i=1}^N{\alpha }_i{y}_i=0\text{\hspace{1em}(22)} \end{gathered}$$
再继续利用拉格朗日乘子法求解式（22）即可得到极值处的${\alpha }_i$了。

有同学会更我当初遇到式（22）一样疑惑，为什么说这个式子变简单了呢？怎么感觉还是很复杂呢？其实对偶算法有一下三点改进：

1. 对偶算法中没有$\vec{\mathbf{w}}$和$b$，这样求解比较简单
2. 对偶算法限制中的${\sum }_{i=1}^N{\alpha }_i{y}_i=0$很容易消去
3. 最重要的是，原算法的限制条件为复杂的线性不等式$y_i(\vec{\mathbf{w}}\overrightarrow{x_i}+b)\ge 1,i=1,2,...,N$，而消去${\sum }_{i=1}^N{\alpha }_i{y}_i=0$的对偶算法，其限制条件为简单的${\alpha }_i\ge 0$，这会极大地降低求解的难度

对于第二点中的${\sum }_{i=1}^N{\alpha }_i{y}_i=0$式如何消去其实很简单，我们总可以将${\alpha }_k$用其他${\alpha }_j,j=1,2,...,N且j\ne k$线性表示。将${\alpha }_k$代入$\frac{1}{2}{\sum }_{i=1}^N{\sum }_{j=1}^N{\alpha }_i{y}_i{\alpha }_j{y}_j{\overrightarrow{x_i}}^T\overrightarrow{x_j}-{\sum }_{i=1}^N{\alpha }_i$中即可。

求出决策边界

我们已经知道${\vec{\mathbf{w}}}^{\ast }={\sum }_{i=1}^N{\alpha }_i{y}_i\overrightarrow{x_i}$，容易看出${\alpha }_i=0$不会影响${\vec{\mathbf{w}}}^{\ast }$，所以为了方便计算挑出${\alpha }_i\ne 0$的向量组成集合
$$K=\{(\overrightarrow{x_k},y_k|{\alpha }_k\ne 0)\}\text{\hspace{1em}(23)}$$
那么${\vec{\mathbf{w}}}^{\ast }$可以改写为：
$${\vec{\mathbf{w}}}^{\ast }=\sum _k^K{\alpha }_k{y}_k\overrightarrow{x_k}\text{\hspace{1em}(24)}$$
如果${\alpha }_i\ne 0$，那么根据KKT条件，则必有$1-[y_i(\vec{\mathbf{w}}\overrightarrow{x_i}+b)]=0$。对于$K$中的向量，都有${\alpha }_i\ne 0$，所以有
$$y_k({\vec{\mathbf{w}}}^{\ast }\overrightarrow{x_k}+b)=1\text{\hspace{1em}(25)}$$
等式两边同时乘$y_k$（$y_k^2=1$），有
$$b=y_k-\vec{\mathbf{w}}\overrightarrow{x_k}\text{\hspace{1em}(26)}$$
因此，只需要在$K$中选择一个样本代入其中即可求解$b^{\ast }$。在实际的数值计算中，人们通常将$K$中所有样本分别求解$b$后取平均得到$b^{\ast }$。

支持向量

其实应该都已经发现${\alpha }_i\ne 0$的向量决定了$\vec{\mathbf{w}}$和$b$，即决定了决策边界，这样的向量我们称为支持向量。因为根据KKT条件，在极值点要满足 α i { 1 − [ y i ( w ⃗ x i ⃗ + b ) ] } = 0 \alpha_i \{1-[y_i(\mathbf{\vec{w}}\vec{x_i}+b)]\}=0 αi​{1−[yi​(w xi​ ​+b)]}=0，同时${\alpha }_i\ne 0$，那么就有
$$1-[y_i(\vec{\mathbf{w}}\overrightarrow{x_i}+b)]=0\text{\hspace{1em}(27)}$$
式（27）表示的是样本在决策边界上，即这些样本是支持向量！

例子

因为现在写博客的进度实在跟不上学习的进度，所以在此偷一个懒，关于例子的话网上有很多，如果有小伙伴们想看详细的有关对偶算法的例子可以在文章下面留言。我尽量再详细讲解一下对偶算法的应用。