emmmm本篇博客主要写了,自己阅读的一些论文,做了一些笔记,主要是记录。
基于深度随机游走的协同过滤推荐算法_刘靖凯
推荐算法:召回和排序
召回步骤常用的算法有协同过滤算法、隐语义算法

常用的协同过滤算法有基于用户的协同过滤算法和基于物品的协同过滤算法,基于用户的协同过滤算法通过推荐与用户兴趣相近的其他用户感兴趣的物品,从而达到精确推荐的目的。
协同过滤算法和基于模型的推荐算法结合,来提高推荐算法的性能
为了保持模型的时效性,一些在线学习的模型通过学习新产生的用户行为数据来保持模型参数的质量。在线学习的推荐模型能够从持续更新的数据流中训练模型参数。常用的模型有增量式的协同过滤模型和增量式的矩阵分解模型。
深度随机游走
深度随机游走是一种将图结构转化为向量表示的算法。算法采用无监督的深度学习方法。深度随机游走算法可以学习到用户节点之间的社交关系,包括相邻用户节点的邻域信息和同一用户群体的成员关系。利用图结构来代替用户的历史行为信息矩阵,可以有效地表示不同用户群体的距离。利用向量来表示用户节点可以有效地解决图数据稀疏性的问题。
基于深度随机游走的协同过滤推荐算法(Collaborative Filtering Algorithm Based on Deepwalk , DW- CF)
利用用户的历史行为,构建用户图结构,计算用户嵌入向量,计算各用户向量间的余弦相似度,从而计算用户的推荐列表,算法在实验中体现了其有效性。
推荐算法利用用户的历史行为数据为用户推荐排序好的物品。

本文推荐算法的思路:根据用户对物品的正反馈行为和用户之间的社交信息,预测每一位用户对物品的兴趣偏好得分 ,从而将预测得分最高的N个物品推荐给用户。
传统的用户协同过滤算法通过计算两盒用户的行为相似度来表示用户之间的兴趣相似度,而本文的深度随机游走算法是通过计算用户的表示向量,计算任意两个向量的余弦距离来表示用户之间的相似度,进而计算用户对物品的兴趣偏好。

基于用户向量的协同过滤算法
基于用户向量的协同锅炉算法是利用上文方法计算得到的用户向量,计算任意两个用户之间的余弦相似度,找到与该用户相似的用户,计算用户对各物品的兴趣得分,为用户推荐物品。与用户k最相似的N个用户L可以通过一下的公式求出
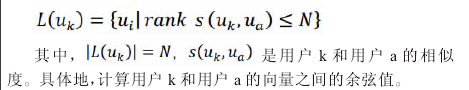
实验与结果分析

实验部分用了公开的数据集MovieLen-IM数据集中包含了一百万条用户对电影的评分记录,用户与电影的交互矩阵稀疏度较大 稀疏度表示了用户与电影交互矩阵R中的非零元素所占比重。


结论:
DW- CF 算法可以有效地学习用户之间的隐向量表示。将用户图结构中产出的随机游走序列作为输入,我们的算法可以有效地学习出包含不同用户群体兴趣偏好的向量表示。将所得向量用于计算用户的推荐列表,可以有效地得到用户对各物品的兴趣偏好,这可以更好的提升推荐系统的准确性。然而,本文提出的算法只适用于静态的用户和物品的数据中,在实际的场景中,用户节点是处于不断变化当中的,如何归纳计算动态的用户向量,是此类推荐算法下一 步研究的重点。
基于选择性随机游走的协同过滤推荐算法研究_单晓菲
论文主要提出了基于选择性随机游走代替传统的pearson相关系数,余弦相似性或者修正的余弦相似度,避免了出度较大的用户与多个用户产生的弱连接。
相关工作介绍
协同过滤算法的基本假设:过去有相似偏好的用户群体在未来也具有相似的偏好
协同过滤推荐算法可以分为四个步骤:测量用户相似度,建立最近邻用户,预测评分,得到推荐列表。算法的关键在于为目标用户找打相似兴趣的最近邻居。用户之间的相似度可以通过使用Pearson相关系数,余弦相似性或者修正的余弦相似性方法。
随机游走是一种数学统计建模,有一连串轨迹组成。
近来被应用于推荐算法的相似性测量中,刘建国等提出基于方向性随机游走的协同过滤推荐,研究用户相似度方向在推荐中的影响。发现用户相似度与用户的出度成反比,



论文中是改变节点的树形设置和选择性随机游走算法的输入参数,指定选择策略,是算法能够适用于推荐系统中的用户——项目网络,而且这种方法只考虑了项目实际评分或者节点出度,在一定程度上造成了信息丢失。论文在游走过程中考虑了项目实际评分,用户出度,项目出度
算法介绍

算法关键在于提高出度较小的用户和项目的影响力,算法使用选择性随机游走计算用户相似度,第二部分预测用户未评价项目的评分
用户相似度计算
用户使用选择性随机游走计算用户相似度,每一次游走,分成三个阶段,步长为二。





项目评分预测

基于复杂网络和随机游走算法的研发项目组合风险分析
测试项目间的连接强度
节点的连接可以分为强连接和弱连接。
强连接指的是网络中直接关联节点之间的联系,弱连接指在网络中由于"邻接节点"的存在而使得节点之间产生连接。

强连接连接强度计算

弱连接强度计算


A Random Walk Model for Item Recommendation in Folksonomies 大众分类法中项目推荐的随机游走模型
本篇论文主要解决社会化标注数据的稀疏问题,但是是2011年的论文,现在可能有更新的解决方法了
摘要:
标签提供了一种可以被推荐系统利用的新型信息。然而,三元<用户、标签、项目>交互数据的稀疏性限制了基于标签的协同过滤的性能。提出了一种基于随机游走的算法来处理社交标签数据的稀疏性问题,该算法通过用户和项目与标签的交互来捕捉用户和项目之间潜在的传递性关联。特别是,从以用户为中心和以项目为中心的角度提出了两种平滑策略。在真实数据集上的实验验证了该算法的有效性。
Social tagging systems allow users to annotate resources (items) with descriptive words of their own choice 社交标签系统允许用户用他们自己选择的描述性词语来注释资源(项目)
数据的稀疏性限制了推荐系统的性能,稀疏性表现为三维用户-项目-标签,论文提出新的基于随机游走的推荐算法,算法利用项目标签、用户标签和用户项目共现信息,利用基于概率的方法来计算用户间和项目间相似度。
Tso-Sutter等人[1]扩展了用户和项目配置文件,以包括用户和项目标签;由此产生的基于用户和基于项目的方法被组合成一种融合方法。
Wetzker等人[4]扩展了概率潜在语义分析(PLSA)方法,并提出了一个基于项目用户和项目标签并行观察的推荐模型。
彭等人[5]提出了一个联合的项目-标签推荐框架,该框架明确指出了用户对推荐项目的兴趣,并充分利用了用户、项目和标签之间的所有可用交互。
基于随机游走的物品推荐
U={u1,u2,u3.....}成为用户的集合,I={I1,I2....}项目的集合,T={t1,t2,t3....}标签的集合,
使用单位、用户界面和信息技术分别表示用户-项目、用户-标签和项目-标签共现矩阵。如果用户i保存项目j,元素UIij在矩阵用户界面中为1,否则为零。UTik表示在UT矩阵用户i使用标签k的频率,
基于游走的方法综述
提出了一种新的概率方法,用于将标签信息结合到项目的计算中和用户的相似矩阵。
项目间和用户间相似性的计算
在论文中使用项目和用户的相似性矩阵作为转移概率矩阵
M. Deshpande and G. Karypis, “Item-based top-n recommendation algorithms”, ACM Transactions on Information Systems (TOIS) , vol. 22, no. 1, pp. 143–177, 2004.这篇论文指出为购买较少项目的用户的购物决策分配更多的权重将提高
(未看完)
随机游走综述
推荐系统可以分为两类,基于内容的和基于协同过滤的
基于内容的系统通过利用从可用上下文中提取的特征来实现这一任务
基于协同过滤使用用户项目子集之间的共享兴趣
此篇论文目的是探索随机游走中的用例,并尝试对它们进行分类。
在抽象意义上,项目表示用户感兴趣的任何东西
推荐系统的思想:找到用户与项目之间的相似度,向用户呈现n个选定的合适的项目,通常是通过将用户与项目的特征表示为一些选定的特征集来实现的,使用数学距离计算方法,计算用户和项目之间的相似度,来找到给定用户的匹配项目。
基于推荐系统在寻找用户和项目之间的关联时所采用的方法,传统上将RSs分为两大类。
基于内容的,系统推荐与用户过去感兴趣的项目,这种兴趣可以用许多方式来表达,例如购买一个项目、点击项目的链接(例如,在电子商务系统中)或者用户在项目的内容上花费的持续时间。例如,如果用户购买了某个具有特定特征的物品,则遥感器可以建议更多具有相同特征的物品作为可能的匹配。
协同过滤:这些系统是基于这样的想法,即与另一个用户有相似品味的用户将拥有两个用户共同感兴趣的项目。两个用户之间的相似性是基于他们的历史来计算的,通常使用购买行为、点击行为等。然后,用户偏好被表示为一组选定的特征,并且使用人与人之间的相关性来找到匹配[2]。
还有其他类型的推荐系统,通常是基于内容和基于内容的方法的衍生或混合。其中一些是基于人口统计、基于知识、基于社区和混合推荐系统[1]。
随机游走
随机游走是在图中运行的结果,在d维整数格,在给定的时间内以定义的概率p向右或者向左移动一步。随机游走问题可以追溯到酒鬼问题
在推荐系统的文献中,随机游走主要是用于马尔科夫模型或者图的环境,总的想法是将给定问题的相关实体和关系表示为图形结构,并推断其他关系以提供有用的建议。
基于推荐系统中随机游走的使用,我们可以识别几个关键类别。
-
Global ranking methods全局排名方法
-
Random walks with restarts重新开始的随机漫步
-
Absorbing random walks吸收随机漫步
Global ranking methods(PageRank算法)
全局排名方法是为整个系统提供单一的元素排名,不能针对个人进行个人偏好定制,PageRank算法
PageRank随机游走是一个随机过程,在任何给定的时间,它都可能在一个特定的节点上,并且在下一个时间步长中,以一个确定的概率,均匀地随机选择一个外边缘,以遍历到下一个节点。
根据以上转移概率的定义,为了使P成为有效的转移矩阵,每个节点必须至少有一条输出链路。
由于像PageRank这样的全局排名方法只能为整个系统提供单一的排名,因此它们不能用于个性化任务。然而,当需要根据重要性对图中的节点进行排序时,这种方法是一种重要的工具。反过来,这样的排名可以用于推荐[12]。
重新开始的随机游走
未完,其他内容在本子上,有时间再记录