一.前言,日常开发中,表单校验是出现率非常高的一个需求,特别是密码校验。本文就针对常见的几种密码校验(含正则)做个总结,做个共享。
二. 密码必须包含数字,字母和特殊符号。
- 写法:
/^([a-zA-Z]+[0-9]+[,._!@#$%^&*]+)|([a-zA-Z]+[,._!@#$%^&*]+[0-9]+)|([0-9]+[,._!@#$%^&*]+[a-zA-Z]+)|([0-9]+[a-zA-Z]+[,._!@#$%^&*]+)|([,._!@#$%^&*]+[a-zA-Z]+[0-9]+)|([,._!@#$%^&*]+[0-9]+[a-zA-Z]+)$/- 案例:

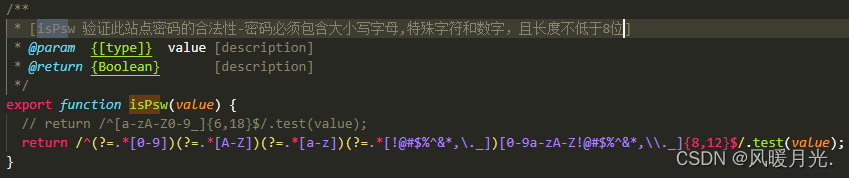
三.密码必须包含大小写字母,特殊字符和数字,且长度不低于8位。
- 写法:
/^(?=.*[0-9])(?=.*[A-Z])(?=.*[a-z])(?=.*[!@#$%^&*,\._])[0-9a-zA-Z!@#$%^&*,\\._]{8,12}$/
- 案例:

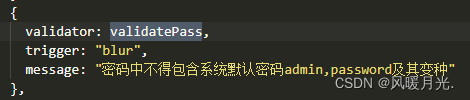
四.密码中不得包含系统默认密码admin,password等及其变种。
- 写法:
const validatePass = (rule, value, callback) => {if (value === "") {callback(new Error("请设置密码"));} else {if (value.includes("admin") ||value.includes("root") ||value.includes("password") ||value.includes("r00t") ||value.includes("weblogic")) {callback(new Error("密码中不得包含系统默认密码admin,password等及其变种"));} else {callback();}}};
- 案例:
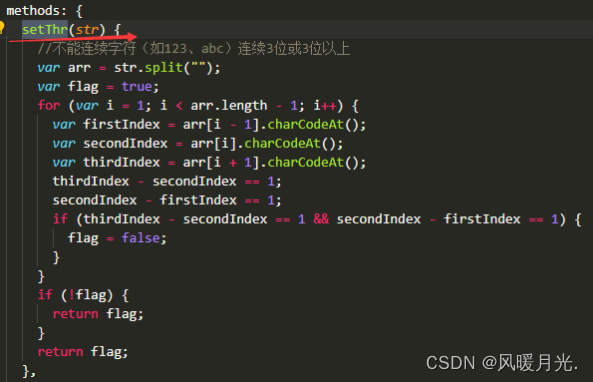
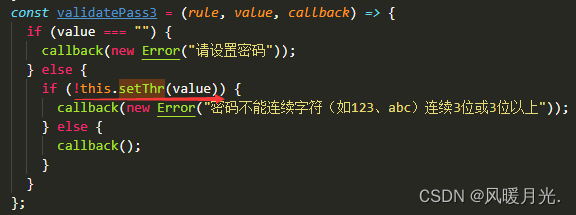
五.密码不能连续字符(如123、abc)连续3位或3位以上。
- 写法:
setThr(str) {//不能连续字符(如123、abc)连续3位或3位以上var arr = str.split("");var flag = true;for (var i = 1; i < arr.length - 1; i++) {var firstIndex = arr[i - 1].charCodeAt();var secondIndex = arr[i].charCodeAt();var thirdIndex = arr[i + 1].charCodeAt();thirdIndex - secondIndex == 1;secondIndex - firstIndex == 1;if (thirdIndex - secondIndex == 1 && secondIndex - firstIndex == 1) {flag = false;}}if (!flag) {return flag;}return flag;},- 案例:

六.密码不能相同字符(如111、aaa)连续3位或3位以上。
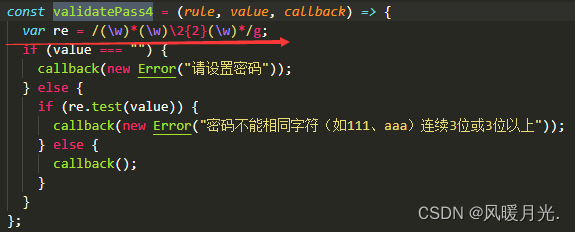
- 写法:
const validatePass4 = (rule, value, callback) => {var re = /(\w)*(\w)\2{2}(\w)*/g;if (value === "") {callback(new Error("请设置密码"));} else {if (re.test(value)) {callback(new Error("密码不能相同字符(如111、aaa)连续3位或3位以上"));} else {callback();}}};- 案例:
七.以上就是本文的全部内容,主要陈列了5种生活中常见的密码校验,包含了密码正则校验的实现方法。感兴趣的童靴,欢迎三连。