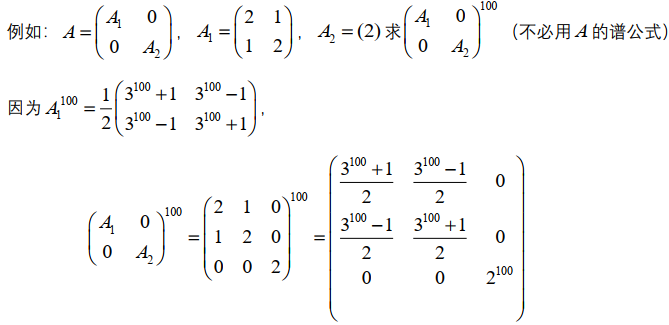矩阵论
1. 准备知识——复数域上矩阵,Hermite变换)
1.准备知识——复数域上的内积域正交阵
1.准备知识——Hermite阵，二次型，矩阵合同，正定阵，幂0阵，幂等阵，矩阵的秩
2. 矩阵分解——SVD准备知识——奇异值
2. 矩阵分解——SVD
2. 矩阵分解——QR分解
2. 矩阵分解——正定阵分解
2. 矩阵分解——单阵谱分解
2. 矩阵分解——正规分解——正规阵
2. 矩阵分解——正规谱分解
2. 矩阵分解——高低分解
3. 矩阵函数——常见解析函数
3. 矩阵函数——谱公式,幂0与泰勒计算矩阵函数
3. 矩阵函数——矩阵函数求导
4. 矩阵运算——观察法求矩阵特征值特征向量
4. 矩阵运算——张量积
4. 矩阵运算——矩阵拉直
4.矩阵运算——广义逆——加号逆定义性质与特殊矩阵的加号逆
4. 矩阵运算——广义逆——加号逆的计算
4. 矩阵运算——广义逆——加号逆应用
4. 矩阵运算——广义逆——减号逆
5. 线性空间与线性变换——线性空间
5. 线性空间与线性变换——生成子空间
5. 线性空间与线性变换——线性映射与自然基分解,线性变换
6. 正规方程与矩阵方程求解
7. 范数理论——基本概念——向量范数与矩阵范数
7.范数理论——基本概念——矩阵范数生成向量范数&谱范不等式
7. 矩阵理论——算子范数
7.范数理论——范数估计——许尔估计&谱估计
7. 范数理论——非负/正矩阵
8. 常用矩阵总结——秩1矩阵，优阵(单位正交阵)，Hermite阵
8. 常用矩阵总结——镜面阵，正定阵
8. 常用矩阵总结——单阵，正规阵，幂0阵，幂等阵，循环阵

---

矩阵分解可以得到简化的乘积矩阵，可以简化后续的计算与处理度

2.4 单阵

单阵A（又叫单纯阵，可对角阵），即满足 $P^{-1}AP=D=\left(\begin{array}{ccc}{\lambda }_1& & 0\\ & \ddots & \\ 0& & {\lambda }_n\end{array}\right)$ ，Q可逆，Q中列向量为A的特征向量

2.4.1 单阵谱公式

若 $A$ 为单阵，全体不同特征根为 ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_k$ ，则有 $A={\lambda }_1{G}_1+\cdots +{\lambda }_k{G}_k$ 为 $A$ 的谱分解

满足性质：

• 谱阵： $G_i=\frac{(A-{\lambda }_1)\cdots (A-{\lambda }_{i-1})(A-{\lambda }_{i+1})\cdots (A-{\lambda }_k)}{({\lambda }_i-{\lambda }_1)\cdots ({\lambda }_i-{\lambda }_{i-1})({\lambda }_i-{\lambda }_{i+1})\cdots ({\lambda }_i-{\lambda }_k)}$，谱阵 $G_1,\cdots ,G_k$ 中各列都是A的特征向量
• 和为单位阵： $G_1+G_2+\cdots +G_k=I$
• 相互正交： $G_1{G}_2=0,\cdots ,G_i{G}_j=0(i\ne j)$
• 幂等： $G_1^2=G_1,\cdots ,G_k^2=G_k$ ，但 $G_1^H=G_1,\cdots ,G_k^H=G_k$ 不一定成立

a. 单阵谱函数

$f(A)=f({\lambda }_1)G_1+\cdots +f({\lambda }_k)G_k$

幂次

$A^p={\lambda }_1^p{G}_1+\cdots +{\lambda }_k^p{G}_p,p=0,1,...$
$$A=\left(\begin{array}{cc}3& 1\\ 2& 2\end{array}\right),求A^{100}$$

由 A 是行和相等矩阵，所以行和 4 为特征值， λ ( A ) = { 4 , t r ( A ) − 4 } = { 4 , 1 } 故二阶阵有 2 个不同特征值，所以必为单阵 G 1 = A − λ 2 I λ 1 − λ 2 = 1 3 ( 2 1 2 1 ) , G 2 = − 1 3 ( 1 − 1 − 2 2 ) 可知 A 100 = 4 100 G 1 + 1 100 G 2 = 本例中，特向 ( 1 1 ) , ( 1 − 2 ) 不正交，不是正规阵 \begin{aligned} &由A是行和相等矩阵，所以行和4为特征值，\lambda(A)=\{4,tr(A)-4\}=\{4,1\}\\ &故二阶阵有2个不同特征值，所以必为单阵\\ &G_1=\frac{A-\lambda_2I}{\lambda_1-\lambda_2}=\frac{1}{3}\left( \begin{matrix} 2&1\\2&1 \end{matrix} \right),G_2=-\frac{1}{3}\left( \begin{matrix} 1&-1\\-2&2 \end{matrix} \right)\\ &可知A^{100}=4^{100}G_1+1^{100}G_2=\\ &本例中，特向\left( \begin{matrix} 1\\1 \end{matrix} \right),\left( \begin{matrix} 1\\-2 \end{matrix} \right)不正交，不是正规阵 \end{aligned} ​由A是行和相等矩阵，所以行和4为特征值，λ(A)={4,tr(A)−4}={4,1}故二阶阵有2个不同特征值，所以必为单阵G1​=λ1​−λ2​A−λ2​I​=31​(22​11​),G2​=−31​(1−2​−12​)可知A100=4100G1​+1100G2​=本例中，特向(11​),(1−2​)不正交，不是正规阵​

单阵逆公式

$A^{-1}=\frac{1}{{\lambda }_1}{G}_1+\frac{1}{{\lambda }_2}{G}_2+\cdots +\frac{1}{{\lambda }_k}{G}_k$ ，其中 $A$ 为单阵

b. 单阵函数公式

若 $f_1(x),f_2(x),\cdots ,f_k(x)$ 为 $x$ 的 $k-1$ 次多项式，且 $f_1(x)+f_2(x)+\cdots +f_k(x)=1$ ，则 $f_1(A)+f_2(A)+\cdots +f_k(A)=I$ ，$f_1(A),\cdots ,f_k(A)$ 中非0列都是 $A$ 的特征向量

2.4.2 单阵判定

a. 充分条件

若存在可逆阵P，使A相似于对角阵，则A为单阵
$$P^{-1}AP=D=\left(\begin{array}{ccc}{\lambda }_1& & \\ & \ddots & \\ & & {\lambda }_k\end{array}\right)$$

1. 单阵特例

   
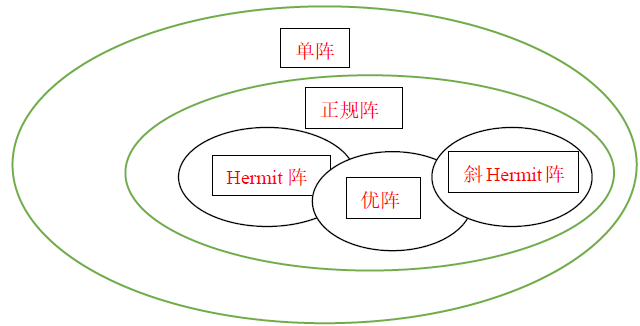
   $A$ 为正规阵，则 $A$ 必相似于对角阵

   证： $A$ 为正规阵，则存在U阵 $Q$ 使 $Q^{H}AQ=\Lambda$ ，使A阵U相似于对角阵，故正规阵一定是单阵

2. 设 $n$ 阶方阵 $A$ 恰有 $n$ 个不同根 ${\lambda }_1,\cdots ,{\lambda }_n$ ，则 $A$ 为单阵（必相似于对角阵）
   证明： λ ( A ) = { λ 1 , λ 2 , ⋯ , λ n } ，则有 A X i = λ i X i , 令 P = ( X 1 , X 2 , ⋯ , X n ) , X i 为 n 维列向量 A ( X 1 , ⋯ , X n ) = ( λ 1 X 1 , ⋯ , λ n X n ) = ( X 1 , ⋯ , X n ) ( λ 1 ⋱ λ n ) ⇒ A P = P D ⟺ P − 1 A P = D \begin{aligned} 证明：&\\ &\lambda(A)=\{\lambda_1,\lambda_2,\cdots,\lambda_n\} ，则有AX_i=\lambda_i X_i ,\\ &令P=(X_1,X_2,\cdots,X_n),X_i为n维列向量\\ &A(X_1,\cdots,X_n)=(\lambda_1X_1,\cdots,\lambda_nX_n)=(X_1,\cdots,X_n)\left(\begin{matrix}\lambda_1&&\\&\ddots&\\&&\lambda_n\end{matrix}\right)\\ &\Rightarrow AP=PD\iff P^{-1}AP=D \end{aligned} 证明：​λ(A)={λ1​,λ2​,⋯,λn​}，则有AXi​=λi​Xi​,令P=(X1​,X2​,⋯,Xn​),Xi​为n维列向量A(X1​,⋯,Xn​)=(λ1​X1​,⋯,λn​Xn​)=(X1​,⋯,Xn​) ​λ1​​⋱​λn​​ ​⇒AP=PD⟺P−1AP=D​

3. A有 $n$ 个无关的特征向量 $X_1,X_2,\cdots ,X_n$

   令 $P=\left(X_1,X_2,\cdots ,X_n\right)\Rightarrow P^{-1}AP=D$

4. 若每个 $k$ 重根 $\lambda$ ，恰有 $k$ 个特征向量，则 $A$ 为单阵

   • 方程 $(A-{\lambda }_1)X=0$ 有 $n-r(A-{\lambda }_{1}I)$ 个基本解 $\Rightarrow AX={\lambda }_{1}X有n-r(A-{\lambda }_{1}I)个基本解$

     常通过判断 $r(A-重根I)$ 判断A是否为单阵

     $\Rightarrow r(A-{\lambda }_{1}I)=n-k$ ，${\lambda }_1$ 有k个特征向量 ，则A可能是单阵

     $\Rightarrow r(A-{\lambda }_{1}I)\ne n-k$ ，则A必不是单阵

   • eg1
     A = ( 1 1 0 0 2 0 0 0 1 ) , λ ( A ) = { 2 , 1 , 1 } ， λ 1 = 1 为 2 重根 A=\left(\begin{matrix} 1&1&0\\0&2&0\\0&0&1 \end{matrix}\right),\lambda(A)=\{2,1,1\} ，\lambda_1=1为2重根 A= ​100​120​001​ ​,λ(A)={2,1,1}，λ1​=1为2重根
     验证A是否为单阵：
     $$\begin{array}{r}A-1I=\left(\begin{array}{ccc}0& 1& 0\\ 0& 1& 0\\ 0& 1& 0\end{array}\right),r(A-I)=1=3-2\therefore A是单阵\end{array}$$

   • eg2
     A = ( 1 1 0 0 1 0 0 0 2 ) , λ ( A ) = { 2 , 1 , 1 } ， λ 1 = 1 为 2 重根 A=\left(\begin{matrix} 1&1&0\\0&1&0\\0&0&2 \end{matrix}\right),\lambda(A)=\{2,1,1\} ，\lambda_1=1为2重根 A= ​100​110​002​ ​,λ(A)={2,1,1}，λ1​=1为2重根
     验证A是否为单阵：
     $$A-1I=\left(\begin{array}{ccc}0& 1& 0\\ 0& 0& 0\\ 0& 0& 1\end{array}\right),r(A-I)=2\ne 3-2=1,\therefore A不是单阵$$

5. 设 ${\lambda }_1,{\lambda }_2,\cdots ,{\lambda }_k$ 为A的全体不同根

   Cayley定理：

   若方阵 $A$ 的特征多项式 $T(x)=|A-xI|=c_0+c_{1}x+c_2{x}^2+\cdots +c_n{x}^n$ ，则 $T(A)=c_{0}I+c_{1}A+c_2{A}^2+\cdots +c_n{A}^n=0$

   • 方阵A的特征多项式可分解为 $T(x)=(x-{\lambda }_1)(x-{\lambda }_2)\cdots (x-{\lambda }_n)$ 满足 $T(A)=(A-{\lambda }_{1}I)(A-{\lambda }_{2}I)\cdots (A-{\lambda }_{n}I)=0$

   若 $(A-{\lambda }_{1}I)(A-{\lambda }_{2}I)\cdots (A-{\lambda }_{k}I)=0$ ，则 $A$ 为单阵( $A$ 相似于对角阵)
   若 $(A-{\lambda }_{1}I)(A-{\lambda }_{2}I)\cdots (A-{\lambda }_{k}I)\ne 0$ ，则 $A$ 不是单阵

   eg
   $$A=\left(\begin{array}{ccc}1& 1& 0\\ 0& 2& 0\\ 0& 1& 1\end{array}\right)是否为单阵，求A^{100}的谱公式$$

   ∣ A − λ I ∣ = ∣ 1 − λ 1 0 0 2 − λ 0 0 1 1 − λ ∣ = ( 1 − λ ) 2 ( 2 − λ ) = 0 , ∴ λ ( A ) = { 1 , 1 , 2 } 令 λ 1 = 1 , λ 2 = 2 , ( A − I ) ( A − 2 I ) = ( 0 1 0 0 1 0 0 1 0 ) ( − 1 1 0 0 0 0 0 1 − 1 ) = 0 ∴ A 为单阵 令 G 1 = A − λ 2 λ 1 − λ 2 = ( 1 − 1 0 0 0 0 0 − 1 1 ) , G 2 = I − G 1 = ( 0 1 0 0 1 0 0 1 0 ) 得谱公式： A = 1 G 1 + 2 G 2 , 且 f ( A ) = f ( 1 ) G 1 + f ( 2 ) G 2 A 100 = G 1 + 2 100 G 2 \begin{aligned} &\vert A-\lambda I\vert=\left | \begin{matrix} 1-\lambda &1&0\\ 0&2-\lambda &0\\0&1&1-\lambda\end{matrix} \right |=(1-\lambda)^2(2-\lambda)=0,\therefore \lambda(A)=\{1,1,2\}\\ &令\lambda_1=1,\lambda_2=2,(A-I)(A-2I)=\left( \begin{matrix} 0&1&0\\0&1&0\\0&1&0 \end{matrix} \right)\left( \begin{matrix} -1&1&0\\0&0&0\\0&1&-1 \end{matrix} \right)=0\\ &\therefore A为单阵\\ &令G_1=\frac{A-\lambda_2}{\lambda_1-\lambda_2}=\left( \begin{matrix} 1&-1&0\\0&0&0\\0&-1&1 \end{matrix} \right),G_2=I-G_1=\left( \begin{matrix} 0&1&0\\0&1&0\\0&1&0 \end{matrix} \right)\\ &得谱公式：A=1G_1+2G_2,且f(A)=f(1)G_1+f(2)G_2\\ &A^{100}=G_1+2^{100}G_2 \end{aligned} ​∣A−λI∣= ​1−λ00​12−λ1​001−λ​ ​=(1−λ)2(2−λ)=0,∴λ(A)={1,1,2}令λ1​=1,λ2​=2,(A−I)(A−2I)= ​000​111​000​ ​ ​−100​101​00−1​ ​=0∴A为单阵令G1​=λ1​−λ2​A−λ2​​= ​100​−10−1​001​ ​,G2​=I−G1​= ​000​111​000​ ​得谱公式：A=1G1​+2G2​,且f(A)=f(1)G1​+f(2)G2​A100=G1​+2100G2​​

   ---

   上述判定方法也适用于分块阵
   $$\begin{array}{r}A=\left(\begin{array}{ccc}2& 1& 0\\ 1& 2& 0\\ 0& 0& 2\end{array}\right)=\left(\begin{array}{cc}{A}_1& 0\\ 0& A_2\end{array}\right),求A^{100}\end{array}$$

   由 A 1 阵为行和阵，特征值 λ ( A 1 ) = { 3 , t r ( A 1 ) − 3 } = { 3 , 1 } ( A 1 − 3 I ) ( A 1 − 2 I ) = ( − 1 1 1 − 1 ) ( 1 1 1 1 ) = 0 , ∴ A 1 为单阵 故有谱分解 A 1 = 3 G 1 + G 2 = 3 A 1 − λ 2 λ 1 − λ 2 I + A − λ 2 I λ 2 − λ 1 = 3 ∗ 1 2 ( 1 1 1 1 ) + 1 2 ( 1 − 1 − 1 1 ) A 1 100 = 3 100 G 1 + 1 G 2 = 3 100 2 ( 1 1 1 1 ) + 1 2 ( 1 − 1 − 1 1 ) A 2 100 = ( 2 100 ) ∴ A 100 = ( A 1 100 A 2 100 ) = ( 3 100 + 1 2 3 100 − 1 2 0 3 100 − 1 2 3 100 + 1 2 0 0 0 2 100 ) \begin{aligned} &由A_1阵为行和阵，特征值\lambda(A_1)=\{3,tr(A_1)-3\}=\{3,1\}\\ &(A_1-3I)(A_1-2I)=\left( \begin{matrix} -1&1\\1&-1 \end{matrix} \right)\left( \begin{matrix} 1&1\\1&1 \end{matrix} \right)=0,\quad \therefore A_1为单阵\\ &故有谱分解 A_1=3G_1+G_2=3\frac{A_1-\lambda_2}{\lambda_1-\lambda_2I}+\frac{A-\lambda_2I}{\lambda_2-\lambda_1}=3*\frac{1}{2}\left(\begin{matrix}1&1\\1&1\end{matrix}\right)+\frac{1}{2}\left( \begin{matrix} 1&-1\\-1&1 \end{matrix} \right)\\ &A_1^{100}=3^{100}G_1+1G_2=\frac{3^{100}}{2}\left( \begin{matrix} 1&1\\1&1 \end{matrix} \right)+\frac{1}{2}\left( \begin{matrix} 1&-1\\-1&1 \end{matrix} \right)\\ &A_2^{100}=(2^{100})\\ &\therefore A^{100}=\left( \begin{matrix} A_1^{100}&\\ &A_2^{100} \end{matrix} \right)=\left( \begin{matrix} \frac{3^{100}+1}{2}&\frac{3^{100}-1}{2}&0\\ \frac{3^{100}-1}{2}&\frac{3^{100}+1}{2}&0\\ 0&0&2^{100} \end{matrix} \right) \end{aligned} ​由A1​阵为行和阵，特征值λ(A1​)={3,tr(A1​)−3}={3,1}(A1​−3I)(A1​−2I)=(−11​1−1​)(11​11​)=0,∴A1​为单阵故有谱分解A1​=3G1​+G2​=3λ1​−λ2​IA1​−λ2​​+λ2​−λ1​A−λ2​I​=3∗21​(11​11​)+21​(1−1​−11​)A1100​=3100G1​+1G2​=23100​(11​11​)+21​(1−1​−11​)A2100​=(2100)∴A100=(A1100​​A2100​​)= ​23100+1​23100−1​0​23100−1​23100+1​0​002100​ ​​

b. 单阵充要条件：0化式判别法(了解，判断用重根矩阵秩)

$$A为单阵⟺极小式m(x)无重根；若m(x)有重根，则A不是单阵$$

0化式与极小式定义

若多项式 $f(x)$ 使 $f(A)=0$ ，则称 $f(x)$ 为 $A$ 的0化式

极小式为次数最少的0化式 ： 若 ${\lambda }_1,\cdots ,{\lambda }_k$ 为不同根，且 $(A-{\lambda }_{1}I)(A-{\lambda }_{2}I)\cdots (A-{\lambda }_{k}I)=0$ ，则 $A$ 必为单阵，此时称 $m(x)=(x-{\lambda }_1)(x-{\lambda }_2)\cdots (x-{\lambda }_k)$ 为 $A$ 的极小式

• eg1：
  $$\begin{array}{rl}& A=I=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right),满足A^2=I，可知f(x)=x^2-1=0,且f(A)=A^2-I=0\\ & f(x)=x^2-1=(x-1)(x+1)为A的0化式\\ & \because A-I=0,\therefore x-1也是A的0化式，且m(x)=x-1为极小式\end{array}$$

• eg2:
  $$\begin{array}{rl}& A=\left(\begin{array}{cc}-1& 0\\ 0& 1\end{array}\right)，A^2=I,即A^2-I=0,\\ & f(x)=x^2-1=(x-1)(x+1)为A的0化式，但由于A-I\ne 0且A+I\ne 0\\ & 故A的极小式m(x)=x^2-1\end{array}$$

极小式求法

1. 对于 $|xI-A|=(x-a{)}^2(x-b)=0$

   • 若 $(A-aI)(A-bI)=0$ ，则极小式为 $m(x)=(x-a)(x-b)$

   • 若 $(A-aI)(A-bI)\ne 0$ ，则极小式为 $m(x)=(x-a{)}^2(x-b)$

2. 对于 $|xI-A|=(x-a)(x-b)(x-c)$ ，则极小式为 $m(x)=(x-a)(x-b)(x-c)$

若f(x)=0无重根，且f(A)=0,则A必为单阵

定理：

• 若 $f(A)=0$ ，则 $f(A)g(A)=0$ ,可知 $f(x)g(x)$ 也是0化式

• 特征多项式 $f(x)=|xI-A|=a_0+a_{1}x+a_2{x}^2+\cdots +a_n{x}^n$ 一定是0化式，即 $f(A)=a_0+a_{1}A+\cdots +a_n{A}^n=0$

• 极小式为特征多项式的因式，可表示为 $|xI-A|=m(x)g(x)$

• 极小式必为每个0化式 $f_i(x)$ 的因子，即若 $f_i(A)=0$ ，则 $f_i(x)=m(x)g_i(x)$

应用

1. 列出特征方程，求出极小式，即证明A是单阵
2. 根据极小式，写出单阵谱分解
3. 计算f(A)

$$A=\left(\begin{array}{ccc}2& 2& 1\\ 1& 3& 1\\ 1& 2& 2\end{array}\right)，求A的谱分解p$$

$$\begin{array}{rl}& \begin{array}{c}|A-\lambda I|=(x-5)(x-1{)}^2,且(A-5I)(A-I)=0\Rightarrow A为单阵\end{array}\\ & \Rightarrow 单阵A有谱分解A=5G_1+G_2=\end{array}$$

---

$$\begin{gathered} A=\left(\begin{array}{ccc}1& 1& 0\\ 0& 2& 0\\ 0& 0& 3\end{array}\right),求谱分解 \\ A为上三角阵，所以A有三个互异特征根1,2,3，极小式为(x-1)(x-2)(x-2)=0 \\ 故A由谱分解A=G_1+2G_2+3G_3 \end{gathered}$$

---

$$\begin{gathered} A=\left(\begin{array}{ccc}1& 1& 0\\ 0& 2& 0\\ 0& 0& 3\end{array}\right),求谱分解 \\ A为上三角阵，所以A有三个互异特征根1,2,3，极小式为(x-1)(x-2)(x-2)=0 \\ 故A由谱分解A=G_1+2G_2+3G_3 \end{gathered}$$