原文:https://jingyan.baidu.com/article/5bbb5a1b634cca53eba179ce.html
-
首先说一下密码必须是6~18位之间的数字,正则表达式为"^[0-9]{6,18}$",其中[0-9]表示必须是数字,{6,18}表示必须在6到18位之间,代码如下:
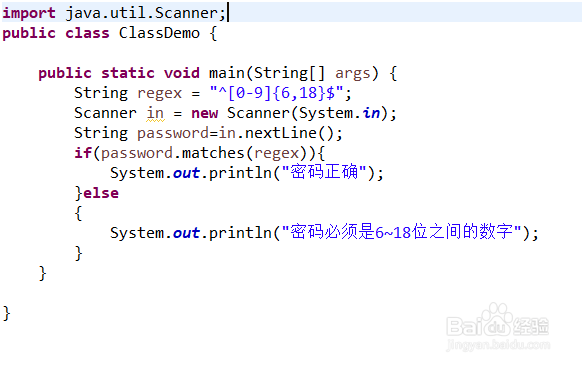
-
运行结果如下
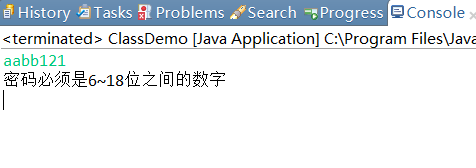
-
接下来是密码中只能包含字母和数字的,正则表达式为:"^(?![0-9]+$)(?![a-zA-Z]+$)[0-9A-Za-z]{6,16}$"其中(?![0-9]+$)表示排除掉只有数字的组合,(?![a-zA-Z]+$)表示排除掉只有字母的组合,[0-9A-Za-z]表示必须有字母或数字,代码如下:
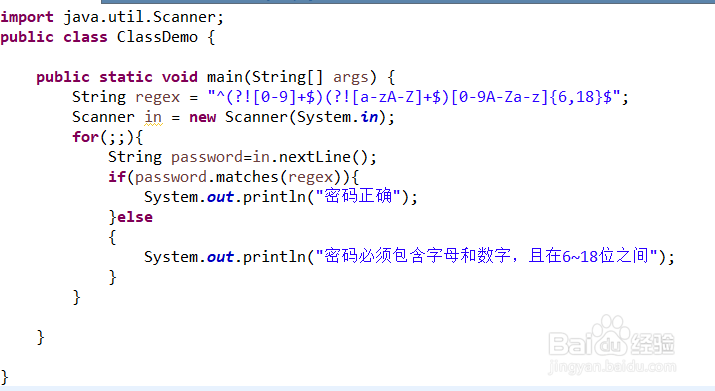
-
运行结果如下:
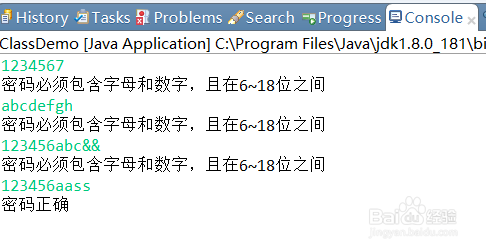
-
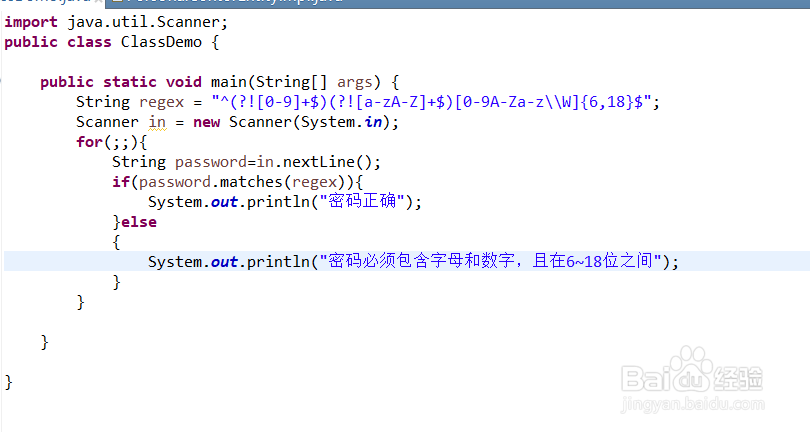
下面说一下密码中可以有(可有可没有)特殊字符的组合,正则表达式为"^(?![0-9]+$)(?![a-zA-Z]+$)[0-9A-Za-z\\W]{6,18}$",其中[0-9A-Za-z\\W]里面的\\W即表示特殊字符,代码如下
-
运行结果如下

-
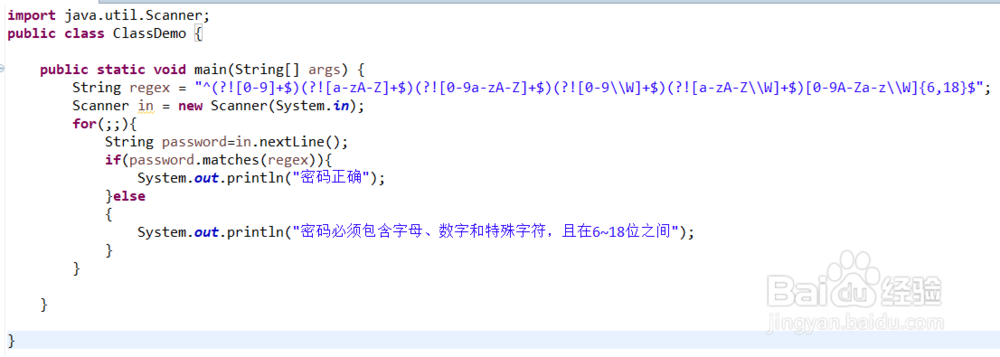
最后介绍一下密码中必须包含字母、数字和特殊字符的,正则表达式为 "^(?![0-9]+$)(?![a-zA-Z]+$)(?![0-9a-zA-Z]+$)(?![0-9\\W]+$)(?![a-zA-Z\\W]+$)[0-9A-Za-z\\W]{6,18}$",其中(?![0-9a-zA-Z]+$)表示排除只有字母和数字的组合,(?![0-9\\W]+$)表示排除只有数字和特殊字符的组合,(?![a-zA-Z\\W]+$)表示排除只有字母和特殊字符的组合,代码如下:
-
运行结果如下

//【全为英文】返回true 否则false boolean result1 = str.matches("[a-zA-Z]+");//【全为数字】返回trueBoolean result6 = str.matches("[0-9]+");//【除英文和数字外无其他字符(只有英文数字的字符串)】返回true 否则falseboolean result2 = str.matches("[a-zA-Z0-9]+");//【含有英文】trueString regex1 = ".*[a-zA-z].*"; boolean result3 = str.matches(regex1);//【含有数字】trueString regex2 = ".*[0-9].*"; boolean result4 = str.matches(regex2);//判断是否为纯中文,不是返回falseString regex3 = "[\\u4e00-\\u9fa5]+";boolean result5 = str.matches(regex3); public static void main(String[] args) {String inpValue = "1111a11111";String regex = "[^a]+";//意思是:匹配不含字符a的其他任意一个或多个字符if (inpValue.matches(regex)){System.out.println("匹配成功");}else {System.out.println("不能字符a");}}public static void main(String[] args) {String inpValue = "11'111\\1";String regex = "[^'\n\r\t\b\f \\\\]+";//意思是:匹配不含这些特殊字符的其他任意一个或多个字符if (inpValue.matches(regex)){System.out.println("匹配成功");}else {System.out.println("不能含特殊字符");}}