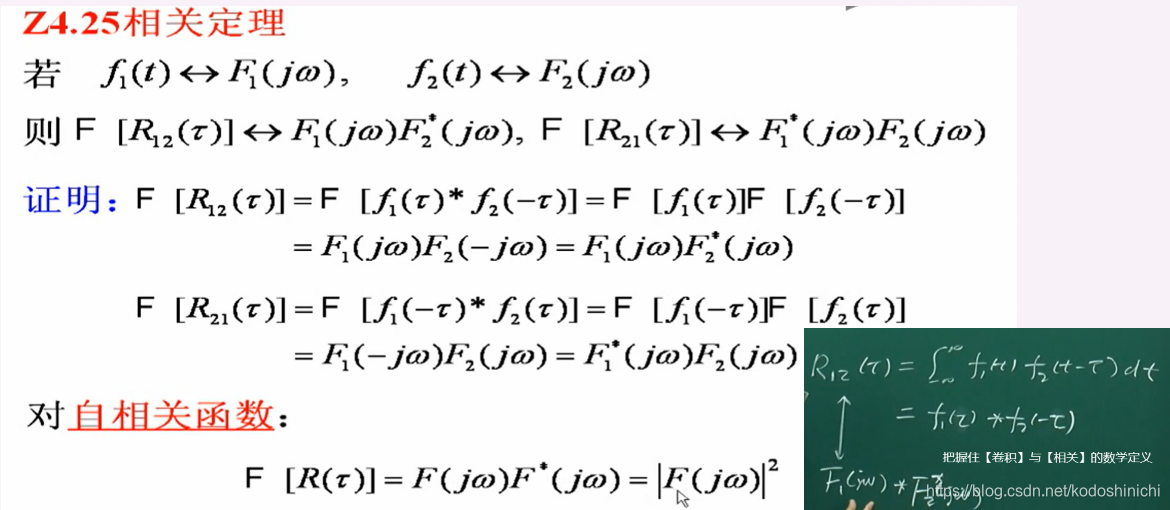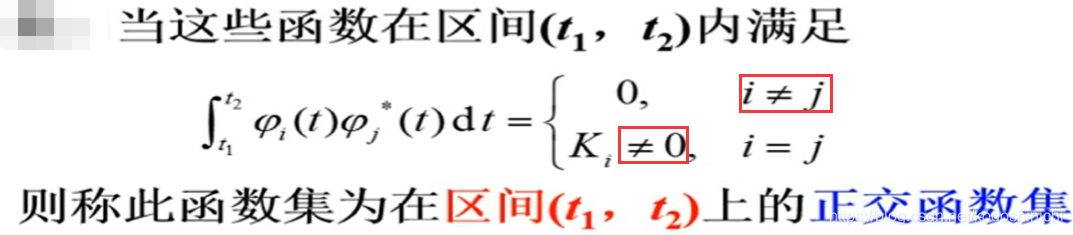信号分解、傅里叶变换与信号谱

信号的分解

在学习【信号分解】这一部分时，脑海里要有两个概念：

• 其一，我们整本书学习的思路就是围绕着将信号分解成基本信号，将系统的响应转变成基本响应这一思路来开展的；
• 其二，我们希望找到一个分解信号的方式，使之分解结果最有效；类比矢量的分解，我们引出对信号的分解。

1. 矢量的正交分解

• ①矢量正交

两个矢量V₁和V₂的夹角为直角↔两个矢量的内积为零，即V₁·V₂=|V₁|·|V₂|·cos90°=0

• ②正交矢量集

由两两正交的矢量组成的矢量集合

p.s. 正交矢量集的概念将正交的位置关系从两个向量拓展到任意多个向量上

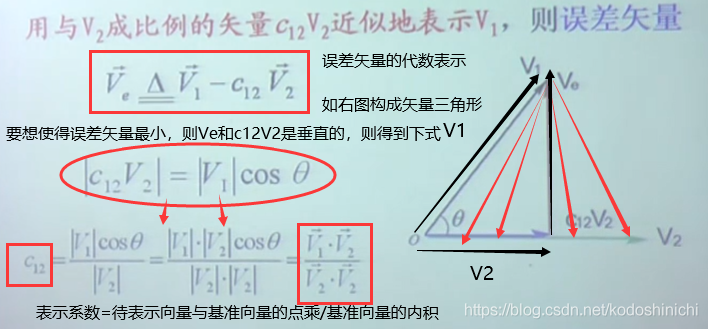
• ③非正交向量的近似表示及误差

现如下图给出一个待表示的向量V₁和基准向量V₂，我们想要在误差最小的情况下将V₁用V₂表示出来：

p.s. 若所选的基准向量V₂与向量V₁是正交的，则无法进行表示。

• ④矢量的正交分解

“任意N维的矢量都可以由N维正交坐标系进行表示”
不管是从线性空间的角度，还是从信息表示的角度——两个相互正交的维度所表示的信息是彼此独立、互不影响的；
因此可以把原向量看成是在各个两两正交维度上分量的矢量叠加；
而待分解的这个向量在各个维度上的分量就可以由上面第③点的公式得出。

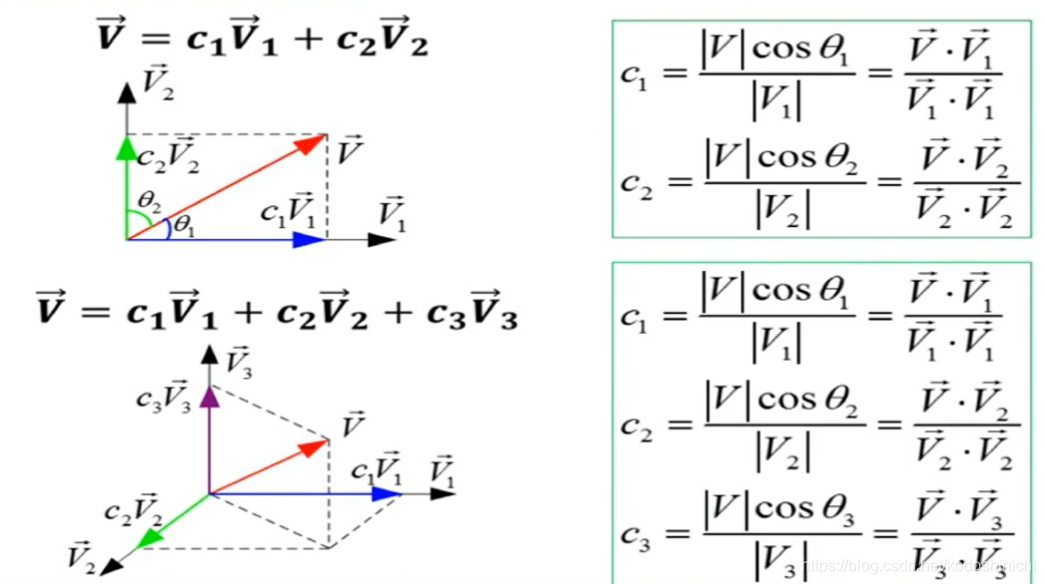
通过上图二维空间与三维空间的分解示例，不难得出：一般地，在n维空间中的任一矢量V，可以精确地表示为n个正交矢量的线性组合，也即
$$V=c_1{V}_1+c_2{V}_2+...+c_n{V}_n$$
式中，V_i·V_j=0(i≠j)，第r个分量的系数为c_r = （V·V_r）/（V_r·V_r）

2. 信号的正交分解

如果我们将信号看成是矢量，则可以平行地将上述【矢量空间正交分解】的概念推广到信号空间中：正交矢量集→正交信号集；
矢量的正交分解与线性表示→信号的正交分解与线性表示。

• ①函数正交
  
• ②函数集

将n个函数φ₁(t)，φ₂(t)，…,φ_n(t)放在一起，即构成了一个函数集：

【正交函数集】该集合内的n个函数在某一区间范围内两两正交

【标准正交函数集】正交函数集内的每个函数自身内积的值为1
【完备正交函数集】其作为一个正交函数集，且具有完备性(除此之外再也找不到和集合内的函数正交的其他函数)


【记忆】两组重要的完备正交函数集（同时也是常用的基本信号），在区间(t₀,t₀+T)(T=2π/Ω)上：

• 三角函数集{1,cos(nΩt),sin(nΩt),n=1,2,…}
• 虚指数函数集{e^jnΩt,n=0,±1，±2，…}

• ③信号的正交分解

p.s. 这里定义的是【广义傅里叶级数】，所谓广义——因为正交函数集{φ_i(t)，i=1,2,…}是任意的，只要满足正交函数集的定义即可。

3.帕斯瓦尔定理

---

傅里叶级数

总结前文，只要我们能够找到一个完备的正交函数集，那么在这完备正交函数集构成的函数空间内的任意函数，都可以表示成集合内各函数分量的线性组合。

三角形式的傅里叶级数

• 三角傅里叶级数与系数
• 狄利赫里条件
• 余弦形式的傅里叶级数
• 吉布斯现象
• 波形对称性与谐波特性

1. 三角傅里叶级数与系数

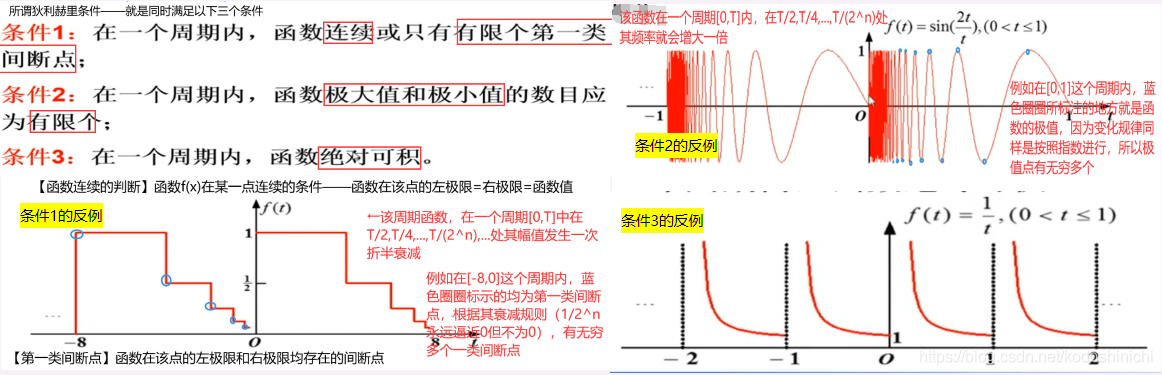
2. 狄利赫里条件

在上图中，讨论三角形式的傅里叶级数的形式以及傅里叶系数的求解公式，其前提是这个周期信号f(t)是满足狄利赫里条件的，先对该条件作出解释：

3. 余弦形式的傅里叶级数

将既含正弦分量又含余弦分量的三角形式的傅里叶级数，写成含有相位信息的余弦分量的表示形式：

4. 吉布斯现象

（1）傅里叶级数分解示例

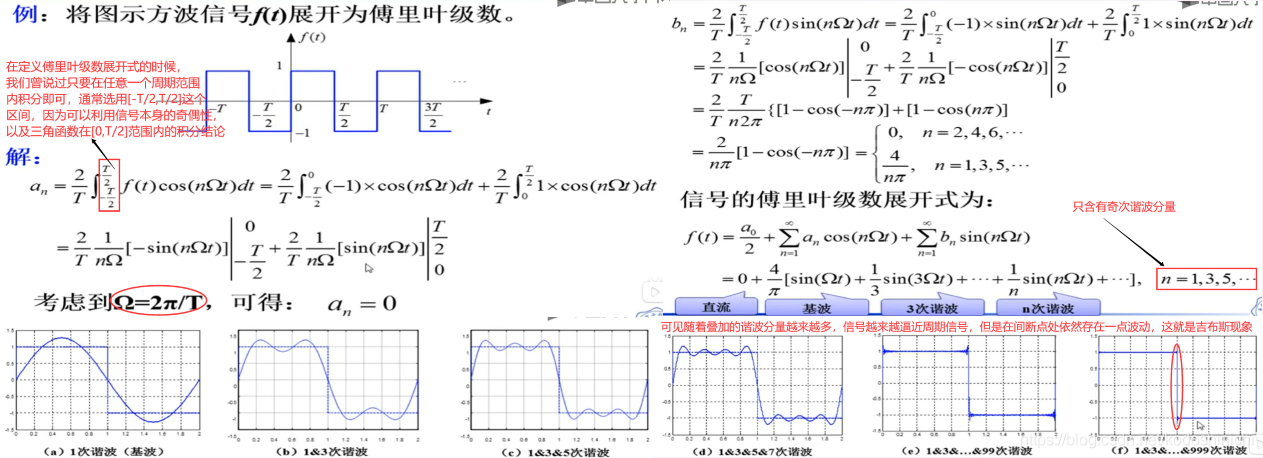
（2）吉布斯现象

5. 周期信号的波形对称性与谐波特性
（1）波形对称性

（2）谐波特性

指数形式的傅里叶级数

1. 展开式与系数结论

2. 指数形式的傅里叶级数推导

两种傅里叶级数之间的关系

---

信号谱

1. 基本描述
我们引入信号【频谱】的概念，实际上是寻求另一个观察信号的视角，不同于时域和空域，从频率的角度来看信号的各分量的基本信息。

• 频谱：周期信号在分解之后，各分量的幅度和相位相对于频率发生的变化；常有幅度谱、相位谱。

拿三角形式的傅里叶展开式为例，任何一个满足狄利赫里条件的周期信号都可以展开成前文所说的三角形式的傅里叶级数，我们就会得到相应的直流、正弦和余弦分量，且具有不同频次的谐波(nΩt)；

对于每一次谐波而言，其都形如A_ncos(nΩt+φ_n)的形式，是典型的三角信号，那么重要的信息就是相位φ_n和幅度A_n；

• 频谱图：将幅度和相位分量用一定高度的直线进行表示；

幅度谱反映了信号不同频率分量的大小——

2. 两种级数对应的信号谱

3. 单边谱与双边谱的关系
（1）关系特点
本质来说，谱图是要看信号的幅度和相位关于频率的变化情况。

那么单边谱(A_n与φ_n)与双边谱(|F_n|和φ_n)关于nΩt（也就是下标n）的关系及其转换，可以通过分析A_n与|F_n|之间的关系，以及φ_n本身的性质来得到。

（2）示例：绘制信号的单/双边谱图

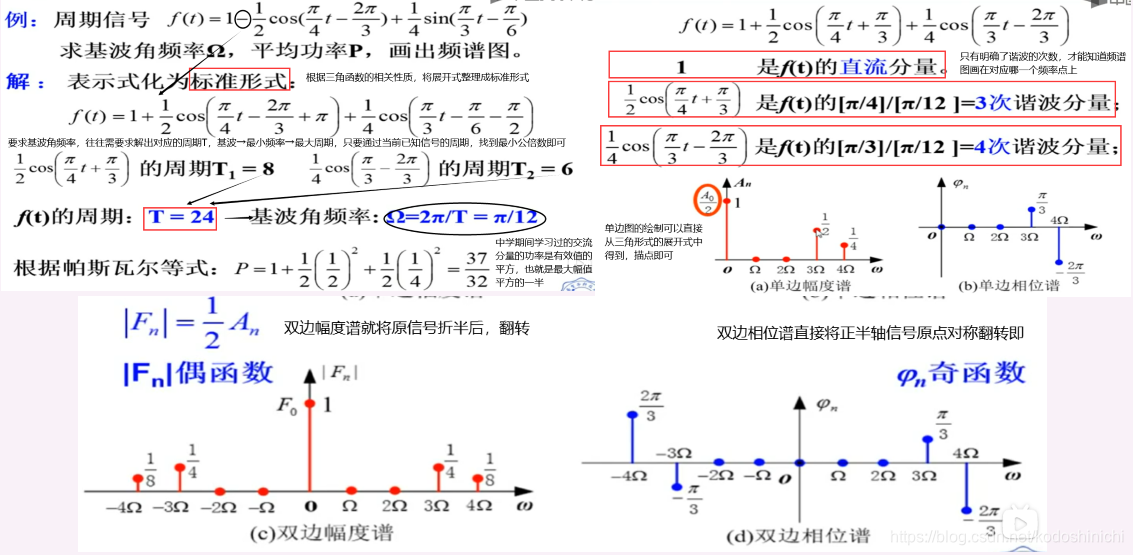
周期信号的信号谱

为了可以更加具象地讨论周期信号频谱的相关特点，我们用一个实例求解进行理解：

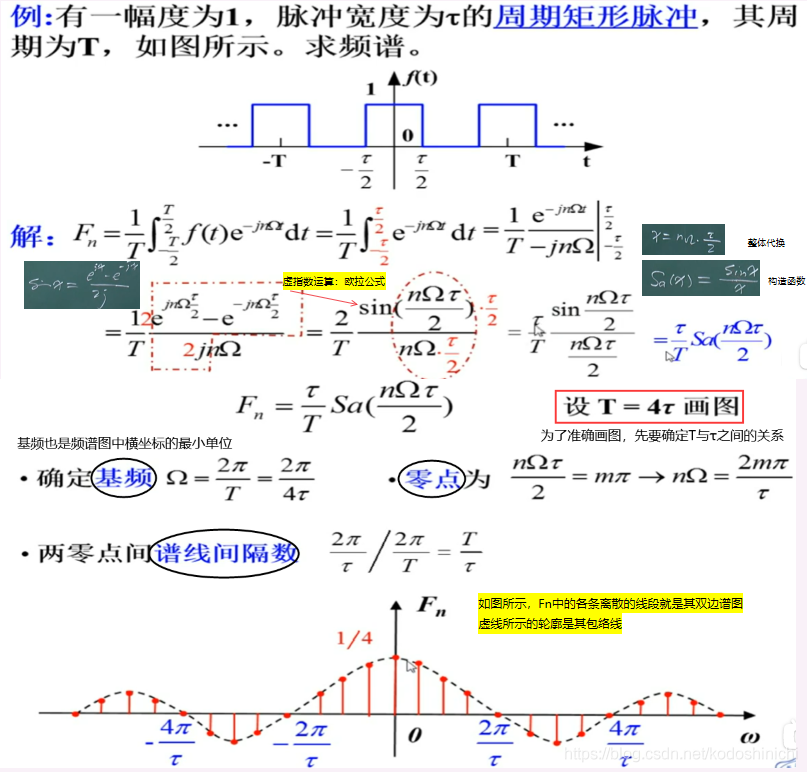
1. 周期信号频谱的特点

• 离散性：以基频Ω为最小间隔的若干离散谱线组成
• 谐波性：谱线值含有基频的整数倍分量
• 收敛性：整体的趋势呈现衰减的趋势
  

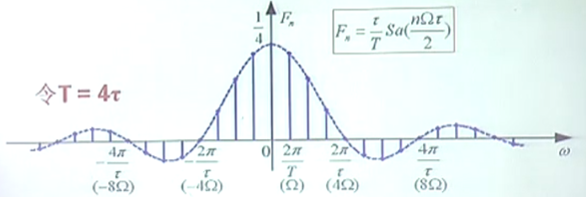
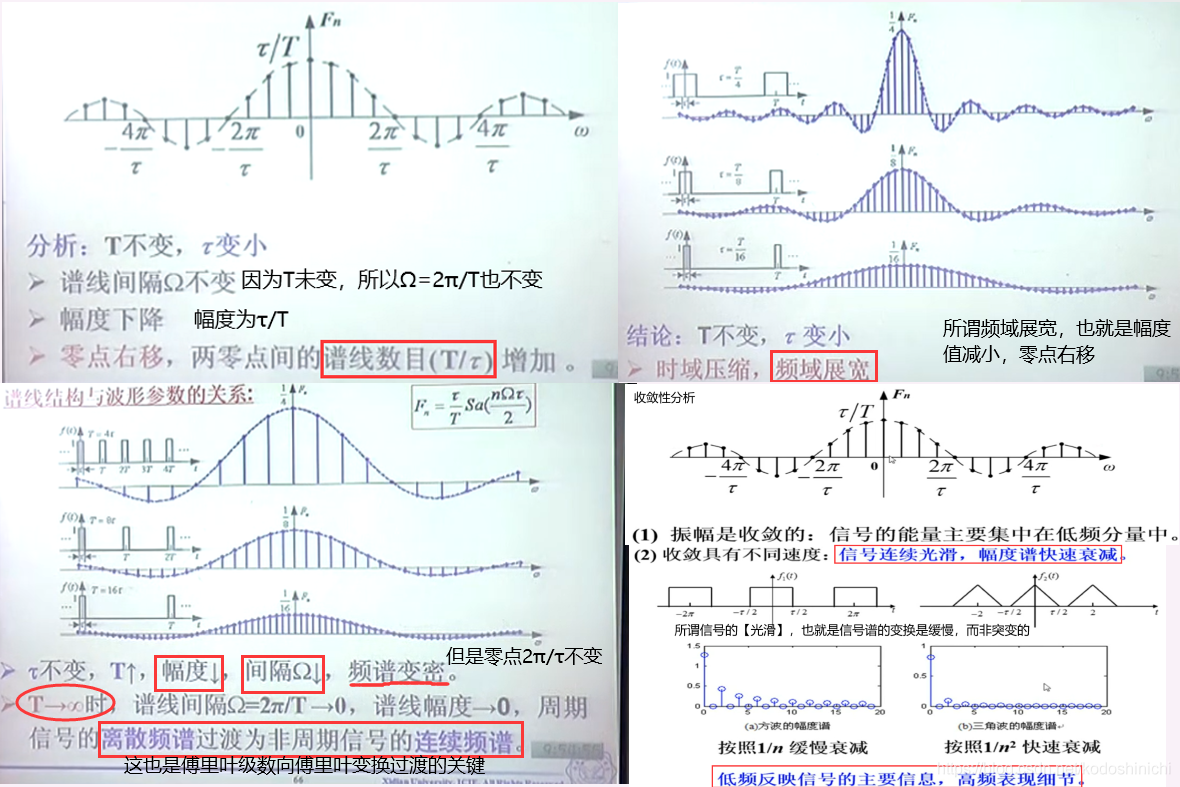
2. 谱线结构与波形参数之间的关系

在上例中，有两个需要关注的谱线参数，分别为信号周期T与脉冲宽度τ；
而对于谱线的结构，我们也主要关注三个量——基波频率Ω、零点位置、以及两个零点之间的谱线数目。

• 当τ发生变化，T不发生变化时——基波频率不变，幅度与τ正相关，零点位置与τ负相关，谱线数目与τ负相关；
• 当T发生变化，τ不发生变化时——基波频率与T负相关，幅度与T负相关，零点位置不变化，谱线数目与T正相关；
• 当T→∞，相当于周期信号变成非周期信号
  

3. 周期信号的功率

（1）功率的求解

（2）频带宽度

非周期信号的信号谱

1. 非周期信号的理解

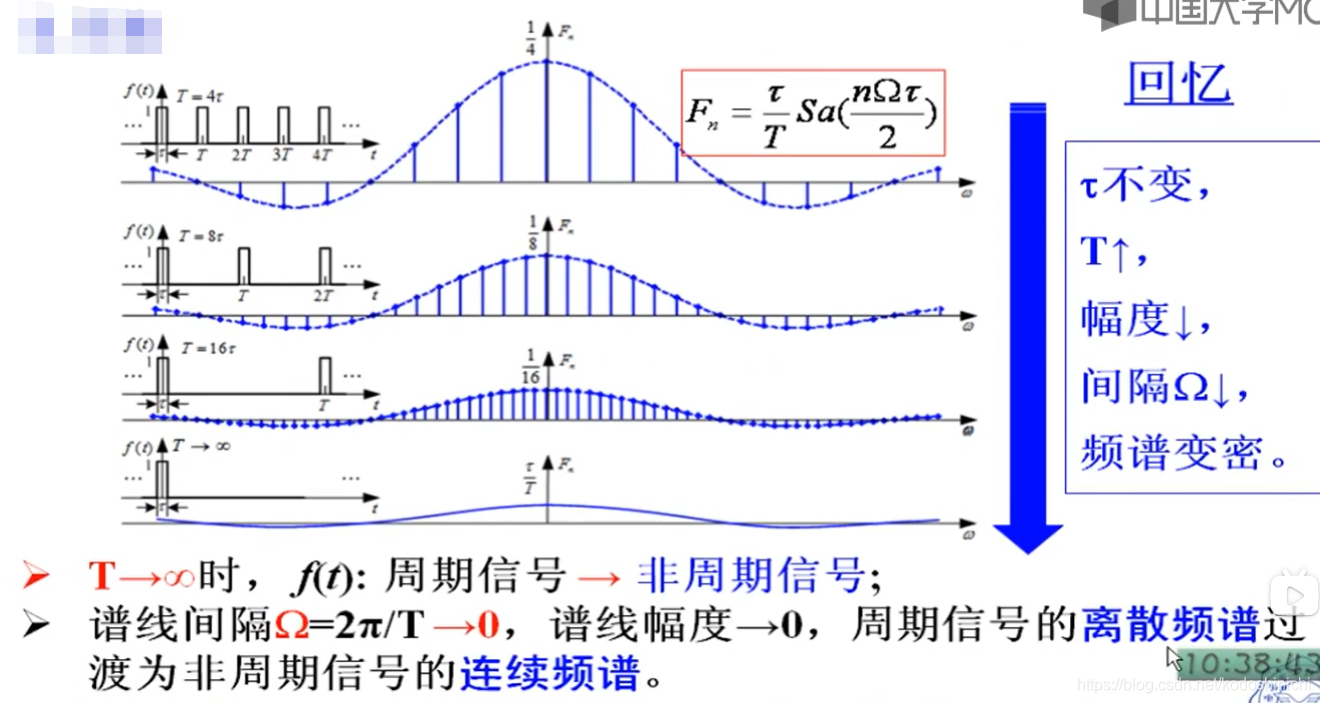
“非周期信号就是周期趋向于无穷大的周期信号”

2. 频谱密度函数

根据上文的讨论，可以知道对于非周期信号而言，其频谱的高度值都是趋向于无穷小的；但是信号在不同频率处的强度依然应该有变化，这个时候，我们需要引出【频谱密度函数】的概念，来比较不同频率信号强度的相对大小。

---

傅里叶变换

在上文中，我们通过讲述周期信号到非周期信号的过渡，引出了频谱密度函数，从而得到了傅里叶变换的形式；
在下文中，我们从数学变换本身的角度，来探讨傅里叶变换的定义、特性与相关结论。

定义与描述

1. 傅里叶变换对

2. 常用函数的傅里叶变换

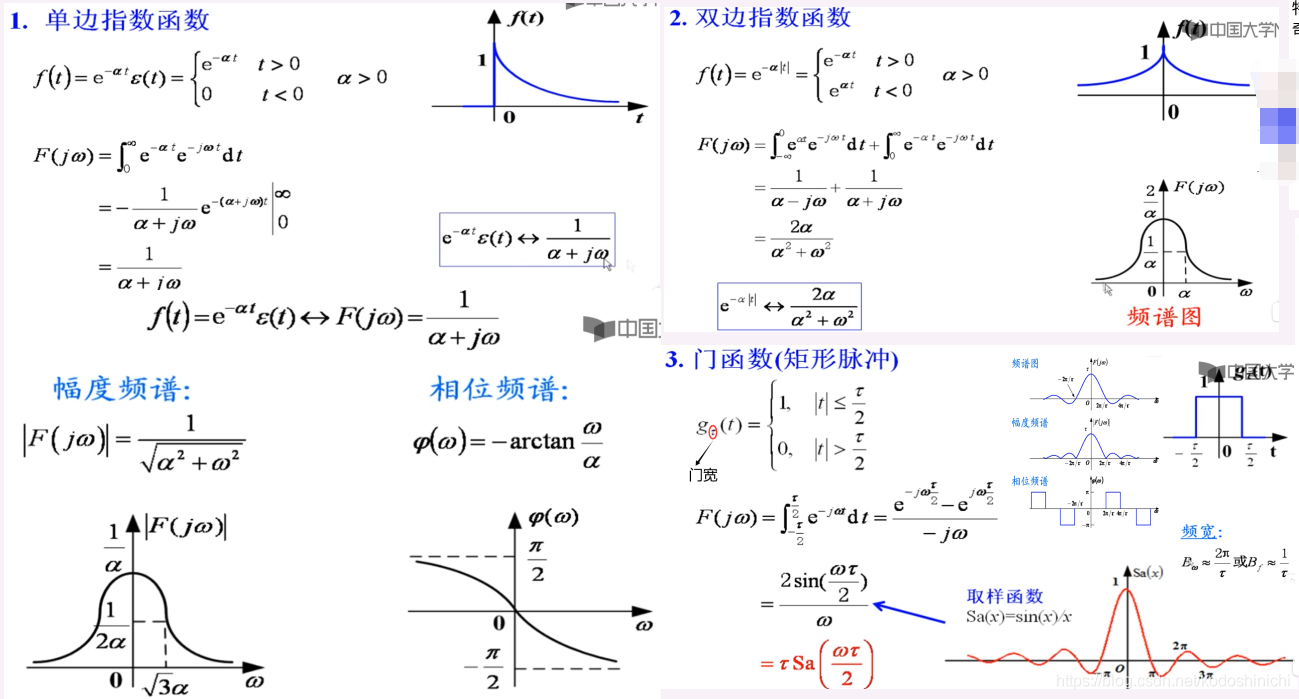
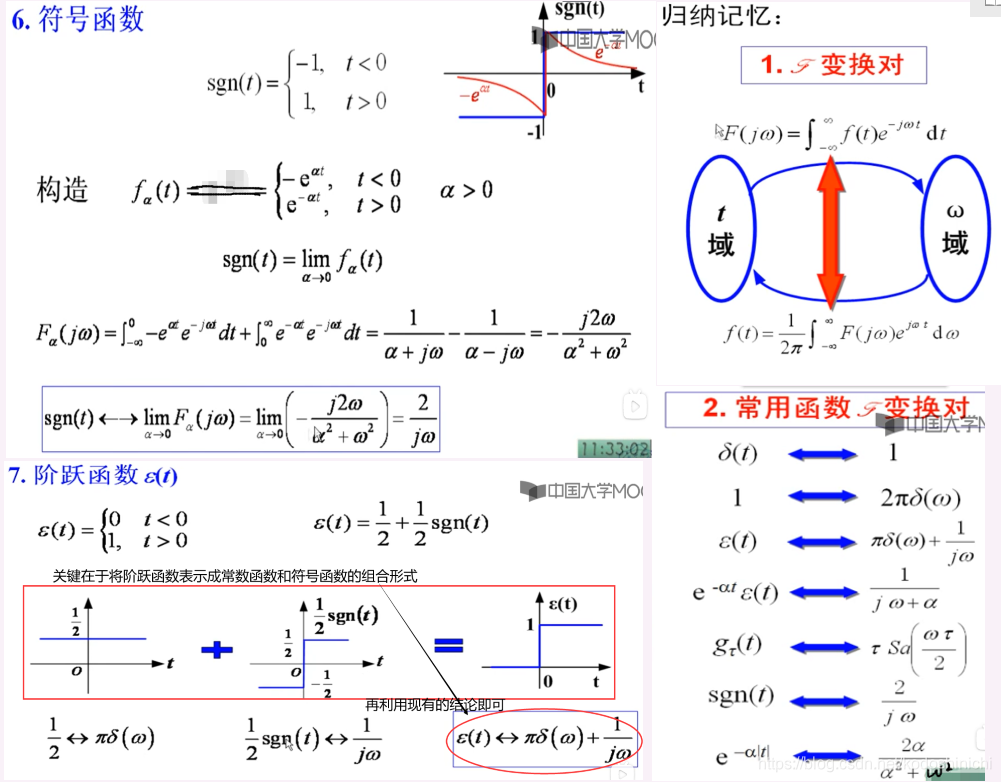
先识记常见到的一些信号的傅里叶变换，后续一些更加复杂的函数就可以转换成基本信号的组合或变换形式，来简化傅里叶变换的求解过程；

而计算常见信号的傅里叶变换，就是直接从定义入手。

性质

下面要讲述的各个性质都是基于上文提到的傅里叶变化对而言的，对于比较复杂的信号傅里叶变换求解问题，常常采用【常见变换结论+性质】的思路；

了解傅里叶变换对的性质，其目的在于——

• 了解时域-频域转换的内在联系
• 利用性质求解复杂信号的变换对
• 了解通信系统中的相关应用

1. 线性性质

2. 奇偶性

当具体地讨论针对不同属性的f(t)，其对应的频谱F(jw)相应有何特点时，根据函数的虚实性、奇偶性会衍生出很多种情况，读者并不需要背下每一种情况。

• 其一，只需要记住R(w)和X(w)的表达式如何推导，以及F(jw)在两种坐标下的表示方式和坐标之间的转化关系；
• 其二，f(t)不论是实函数还是虚函数，其对应的F(jw)都会出现虚实两种情况——
  F(jw)的奇偶性与f(t)的奇偶性保持一致；
  f(t)为实函数和虚函数时，其F(jw)的虚实对应关系恰恰相反。

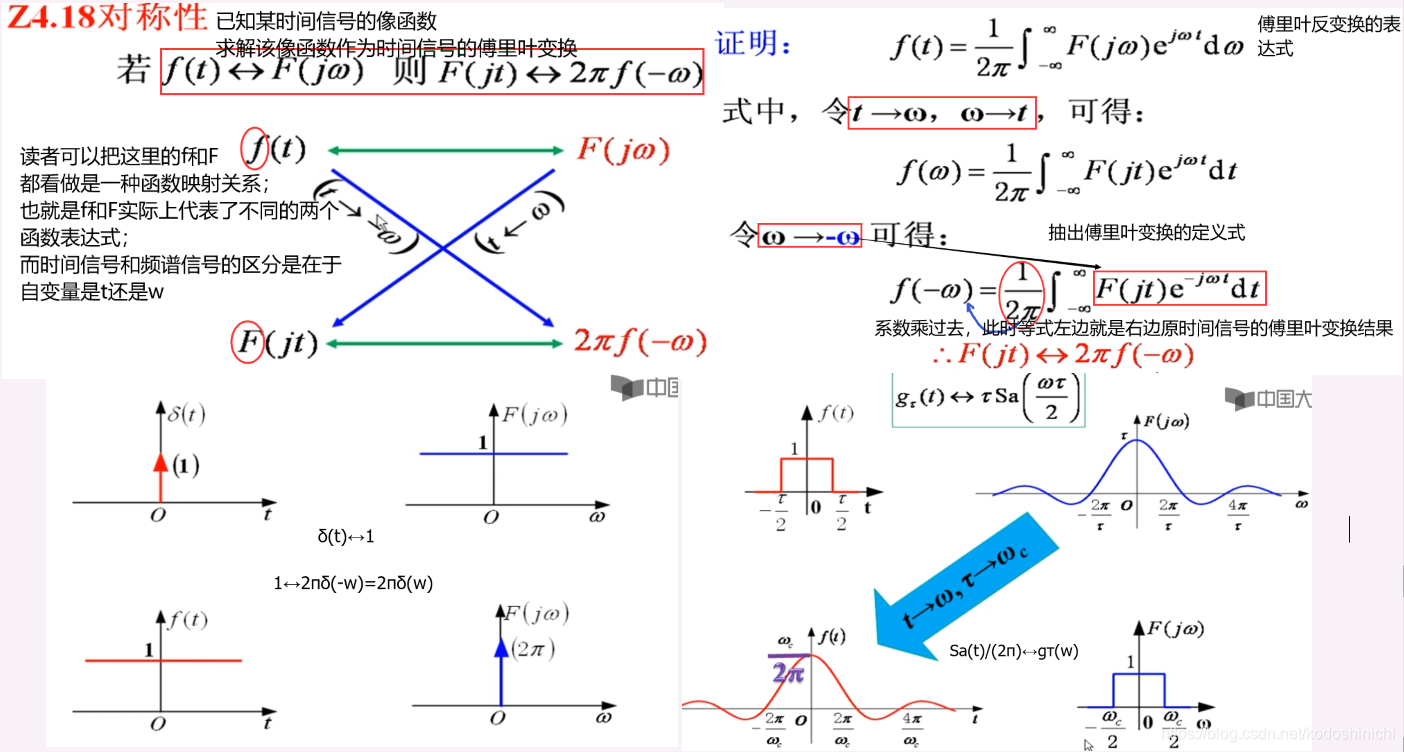
3. 对称性

4. 尺度变化特性

5. 时移特性

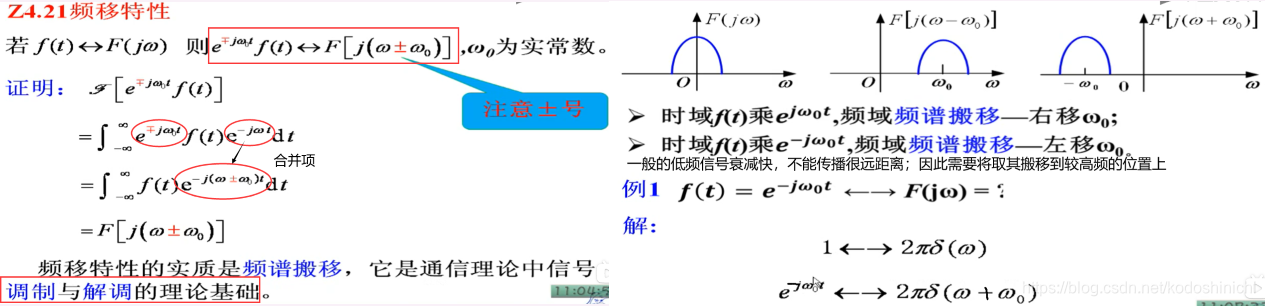
6. 频移特性

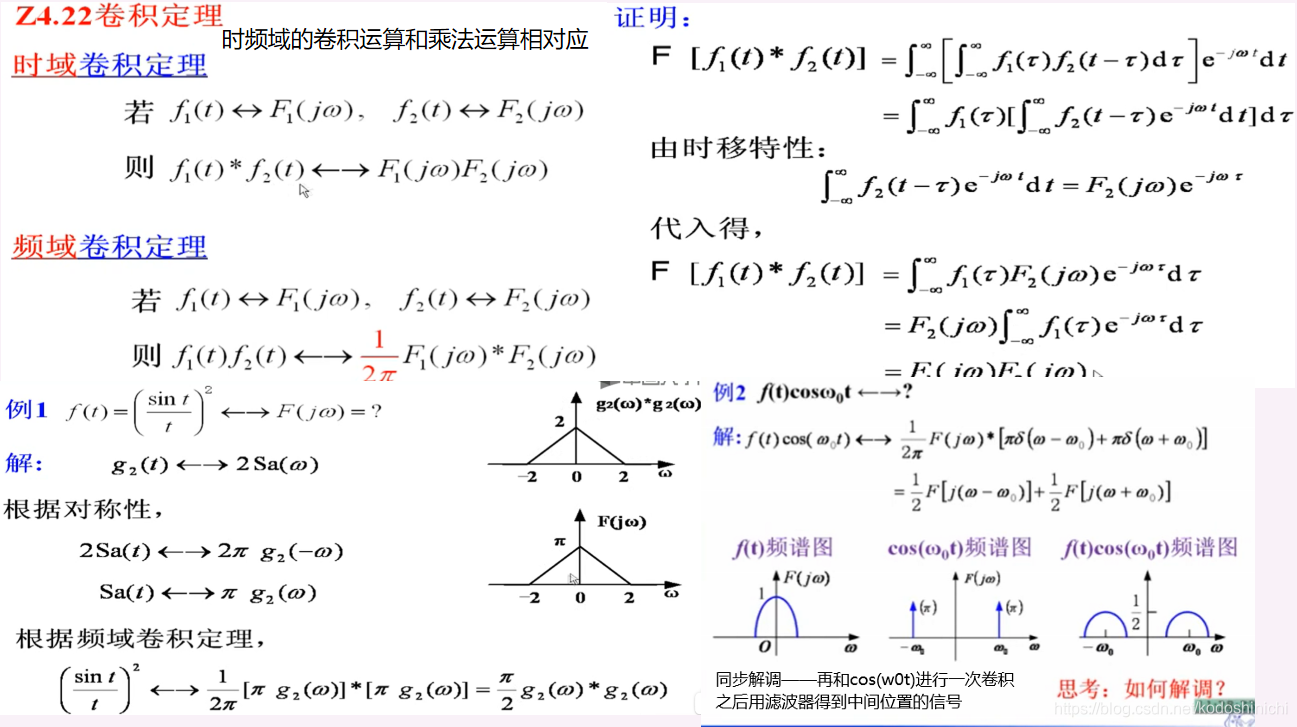
7. 卷积定理

8. 时域微积分特性

9. 频域微积分特性

相关定理