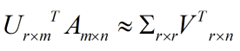遍历保密速率（ergodic secrecy rate）

说遍历容量不十分准确，应该叫各态历经性容量。是相对于中断容量说的。
理解这个概念不太容易的，首先要理解《信息论》中得香农信道容量，然后结合《随机过程》这门课的内容来理解。通常我们所说的香农容量是在确定性信道条件下得到的信道容量，是一个确定值。但实际上，信道状态是一个不断变化的随机过程，应该采用统计意义上的信道容量来描述。有两种统计意义上的描述方式：
1）各态历经信道容量 2）中断信道容量。
其中，各态历经容量是指随机信道在所有衰落状态下的最大信息速率的时间平均，各态历经容量适用于研究时延不敏感业务，如Email，用来确定最大长期平均传输速率。由于各态历经容量要求业务编码帧很长，显然不适用于语音等具有严格时延要求的业务。对于这类业务，编码帧长度只能跨越有限个信道衰落状态，传统的Shannon容量为0。只能定义中断容量，当以此作为传输速率时，信道能以(1-p％)的概率承载。即其中p为允许的中断概率。

香农容量为遍历， 而带中断的容量：即指定中断率下信道能传送的最大恒定传输速率
由于发送端不知信噪比的值，所以只能以一个不依赖瞬时信噪比的固定速率传输 允许以一定概率译错所传输比特，发送端确定一个最小接收信噪比r0，由此确定速率C=Blog(1+r0)。若接收的瞬时信噪比大于或等于r0，则正确译码，否则将出现中断。出现中断的概率Pout=P(r<r0)，正确传输的概率1-Pout，平均正确接收的数据速率(1-Pout)Blog(1+r0)。

闭式解（解析解）和数值解

闭式解

是在特定条件下通过近似计算得出来的一个数值，而解析解为该函数的 解析式 。
解析解(analytical solution)就是一些严格的公式更general，给出任意的自变量就可以求出其因变量，也就是问题的解, 他人可以利用这些公式计算各自的问题.

数值解

就是用数值方法求出解，给出一系列对应的 自变量 和解
数值解(numerical solution)是采用某种计算方法,如有限元的方法, 数值逼近,插值的方法, 得到的解.别人只能利用数值计算的结果, 而不能随意给出自变量并求出计算值.

拉普拉斯变换

拉氏变换是一个线性变换，可将一个有参数实数t（t≥ 0）的函数转换为一个参数为复数s的函数。

傅里叶：各种正弦函数组合的结果——告诉我们某个位置正弦波的强度

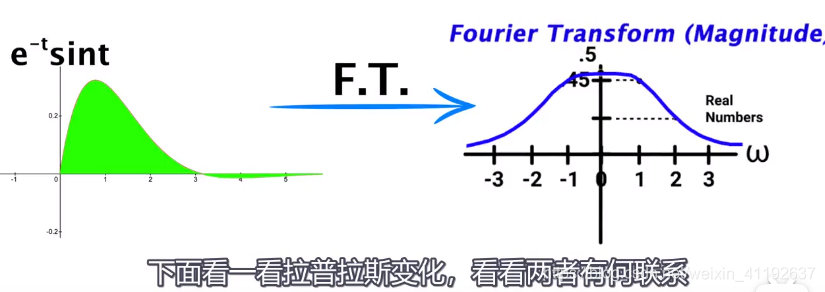
谱分解/正交分解