---

一、数值微积分

1.1 数值计算与符号计算的区别

数值计算：必须先对变量赋值，然后才能参与运算，运算结果是数值
符号计算：无须事先对变量赋值，而将所得到的结果以标准的符号形式来表示
符号计算的特点：

1. 运算对象可以是没有赋值的符号变量
2. 以推理解析的方式进行运算，因此不受计算误差累积所带来的困扰

1.2 符号对象

任何符号对象都必须借助专门的sym或syms定义

syms % 是定义符号变量
sym % 是将字符或者数字转换为字符
sys('a+b') % 就是将a+b转化为符号表达式

任何包含符号对象的表达式、方程也一定是符号对象

1.3 符号常量

当数值常量作为sym（）的输入参量时，就建立了符号常量
虽然看上去是一个数值量，但已经是一个符号对象了

1.4 符号变量

符号变量是内容可变的符号对象
符号变量的命名规则和数值变量的命名规则相同

1.4.1 符号变量的创建

1. 单个符号变量创建函数sym

x = sym('a') % 符号变量x的值为a，默认为复数(flag)
x = sym('value', 'flag') % 符号变量x的值为value，flag为数值域（复数、实数、正数）
real -> 实数
positive -> 正数

1. 多个符号变量创建函数syms

syms x a b real

1.4.2 创建符号矩阵

>> A = sym('[a,b;c,d]')
A =[ a, b]
[ c, d]>> syms a b c d
>> B = [a, b ; c, d]B =[ a, b]
[ c, d]>> B = [a b ; c d]B =[ a, b]
[ c, d]

1.4.3 自由符号变量

解题围绕该变量进行
ax²+bx+c = 0
默认自由符号变量为x

1.5 符号表达式

1. 符号表达式是由符号常量、符号变量、符号函数运算符以及专用函数连接起来的符号对象
2. 符号表达式包括：符号函数与符号方程
3. 区别：符号函数不带等号，符号方程带等号

1.6 符号计算的运算符

关系运算符只有：

== 与 ~=

1.7 符号运算中的函数运算

1. 三角函数和双曲函数
   除atan2外语数值运算相同
2. 指数和对数函数
   没有log2和log10
3. 复数运算
   没有提供相角的命令
4. 矩阵代数命令
   与数值运算相同

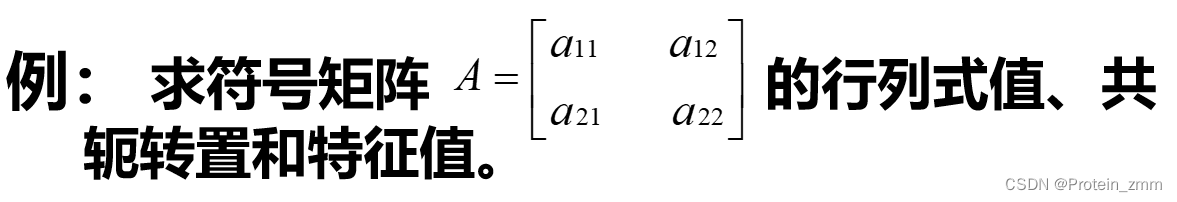
>> syms a11 a12 a21 a22
>> A = [a11 a22 ; a21 a22]A =[ a11, a22]
[ a21, a22]>> det(A) % 计算行列式的值ans =a11*a22 - a21*a22>> A' % 计算转置ans =[ conj(a11), conj(a21)]
[ conj(a22), conj(a22)]>> eig(A) % 计算特征值ans =a11/2 + a22/2 - (a11^2 - 2*a11*a22 + a22^2 + 4*a21*a22)^(1/2)/2a11/2 + a22/2 + (a11^2 - 2*a11*a22 + a22^2 + 4*a21*a22)^(1/2)/2>> 

1.8 符号计算与数值计算的区别

（1）数值计算保留8位有效位数,每一次数值计算有一定的截断误差，重复的多次数值计算就可能会造成很大的累积误差；符号计算不进行数值计算，无截断误差。
（3）符号计算的时间较长，而数值计算速度快。
（4）数值计算中必须先对变量赋值；符号计算无须事先对变量赋值，但必须先定义，计算结果以标准的符号表达式形式给出。

二、符号数字及表达式

2.1 数值数字变符号数字

S = sym(A)
Sc = sym(A, flag)
flag:
有理分数'r'
十进制数'd'
浮点数'f'
估计误差'e'

2.2 符号数字变数值数字

2.2.1 符号数值变数值数字

number = double(number_sys)

2.2.2 符号矩阵转化为数值矩阵

B = eval(A)

2.2.3 符号计算精确度转化函数vpa(x,n)

vpa(x,n)

x是符号或者数值，有效位数是n位（默认是32）

2.3 化简各种表达式simplify

simplify(S)

将S转化为最简短形式

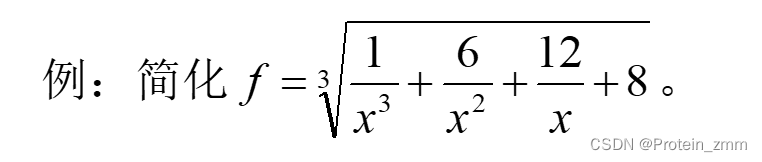
>> syms x;
>> f=(1/x^3+6/x^2+12/x+8)^(1/3);
>> simplify(f)ans =((2*x + 1)^3/x^3)^(1/3)

2.4 符号表达式的置换操作

2.4.1 子表达式置换操作subexpr（自动替换）

[RS,ssub]=subexpr(S,ssub)

从表达式S中自动提取公因子，记为ssub；
并将ssub置换S中的因子因子，重写S为RS

2.4.2 子表达式置换操作subs（人为操作）

R=subs(S,Old,New) 

新符号变量New替代原来符号表达式S中的变量Old
数值代替所有符号变量则结果转化为数值数据。

>> syms x y
>> ss=x-sin(x)-1/sin(x);
>> subs(ss, sin(x), y)ans =x - y - 1/y

多重替换

R=subs(S,{Old1, Old2…},{New1, New2…}) 

三、符号微积分

3.1 符号表达式F的极限limit

limit(F,x,a) % 默认自变量x趋近于a的极限

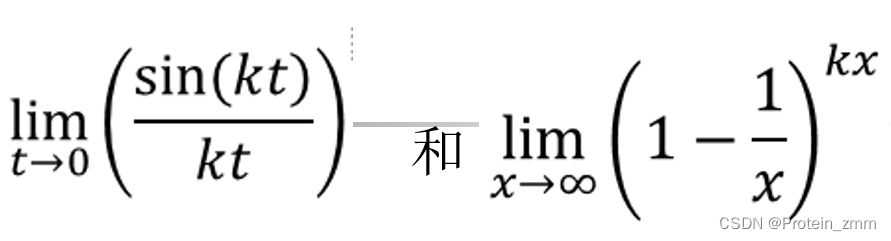
>> syms k t
>> ss = sin(k*t) / (k*t);
>> limit(ss, t, 0)ans =1>> syms k x
>> ss = (1-1/x)^(k*x);
>> limit(ss, x, inf)ans =exp(-k)

3.2 符号表达式F的求导diff

diff(F,v,n) % 自变量v的n阶导

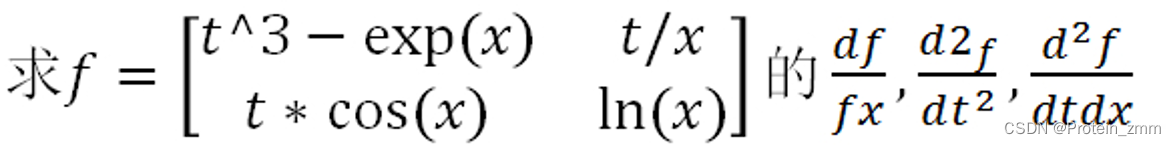
>> syms x t
>> f=[t^3-exp(x),t/x;t*cos(x),log(x)]f =[ t^3 - exp(x),    t/x]
[     t*cos(x), log(x)]>> diff(f,x,1)ans =[   -exp(x), -t/x^2]
[ -t*sin(x),    1/x]>> diff(f,t,2)ans =[ 6*t, 0]
[   0, 0]>> diff(diff(f, t, 1), x, 1)ans =[       0, -1/x^2]
[ -sin(x),      0]

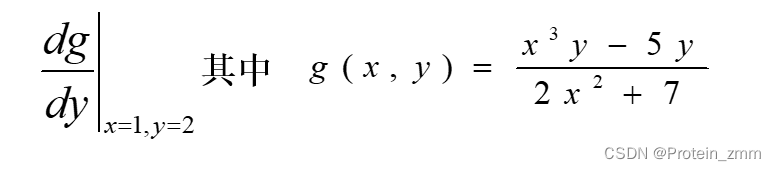
>> syms x y
>> g=(x^3*y-5*y)/(2*x^2+7);
>> gy = diff(g, y, 1);
>> subs(gy, [x, y], [1, 2]) % 用1,2去替换x，yans =-4/9

3.3 符号表达式F的积分int

int(F,v,a,b) % 自变量v从a到b的定积分
int(F,v) % 自变量v的不定积分

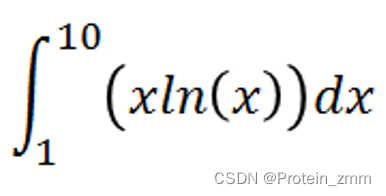
>> syms x
>> int(x*log(x), x, 1, 10)ans =50*log(10) - 99/4

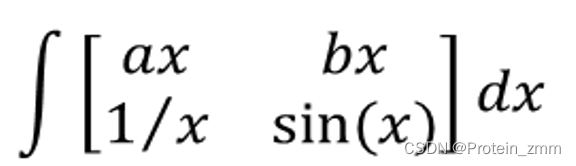
>> syms a b x
>> f = [a*x, b*x; 1/x, sin(x)];
>> int(f, x)ans =[ (a*x^2)/2, (b*x^2)/2]
[    log(x),   -cos(x)]

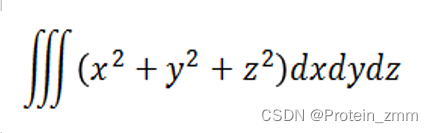
>> syms x y z
>> f = x^2 + y^2 + z^2;
>> int(int(int(f,x),y),z)ans =(x*y*z*(x^2 + y^2 + z^2))/3

3.4 级数求和symsum

symsum(F,v,a,b) % 变量v从a到b的和
symsum(F) % 默认自变量x的区间[0, v-1]求和

>> syms n
>> f = 1 / (2*n-1)f =1/(2*n - 1)>> r = symsum(f, n, 1, 100);
>> double(r) % 将符号数字转化为数值数字ans =3.2843

3.5 泰勒级数taylor

r=taylor(f,v,a,'Order',n) % 表达式f对自变量v在a处的n阶泰勒展开式。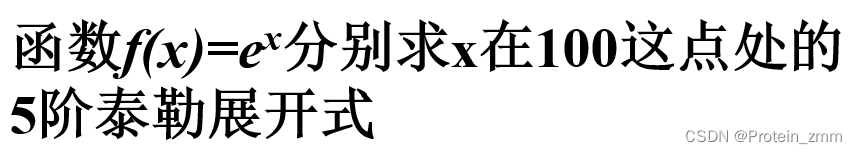

>> syms x
>> taylor(exp(x), x, 100, 'order', 5)ans =exp(100) + exp(100)*(x - 100) + (exp(100)*(x - 100)^2)/2 + (exp(100)*(x - 100)^3)/6 + (exp(100)*(x - 100)^4)/24

四、符号方程求解

4.1 符号方程

字符串型
s=solve(‘eq1’,’eq2’,…,’eqn’,’var1’,’var2’,…,’varn’) 
符号型
s=solve(exp1, exp2,…, expn,var1,var2,…,varn)

‘eq1’,…,’eqn’：字符串表达的方程 ；
exp1,…,expn：符号表达方程 ；
’var1’,…,’varn’：求解变量名, 省略时symvar确定n个变量；
S：方程组的解，是一个架构数组
若字符串表达的方程 eqn 中不含等号，则表示解方程 f=0

 [x,y,z] = solve('s+y+z=1', 'x-y+z=2', '2*x-y-z=1',x,y,z)x =1 - s/2y =-(3*s)/4z =1 - s/4