Abstract
引言
在这篇文章里。我主要介绍一些经典的PID参数整定方法。也会努力查找文献给大家介绍一些参数整定方面的最新研究,这次文章可能会分批次完善,请大家谅解。
从构思到拖更,过了一两月,请大家见谅,这个部分稍微比较复杂,需要大量的文献调研。想坚持给大家写一些真实有用的东西。
这篇文章会逐步完善。
手动调参
不管喜不喜欢,这大概是最直接的方法了吧。😄
一个榔头敲一个钉子,请时刻记住,我们现在要整定的参数,是电机闭环控制的参数。先来说一说电流环,我们从电流环的参数整定开始讲起。这里要事先了解一些参数,我做实验用的电机是24V的,假设现在有负载,工作电流最大为0.5A。而我们的PWM是的比较值为-65535到655535(正反转)。我们知道,0.1A对于我当前的电机而言,是一个很大的输入电流。回到闭环控制上来,我们用误差(测量值-期望值)来控制输出,PID控制器在其中充当了调节器的作用。再回到PID的公式:
Out = Err*Kp + ∑Err*Ki + (Err-Last_Err)*Kd
先假设我们只使用Kp来控制输出,即我们的输出电流是得到的电流误差乘上一个比例因子,实际测量(用手干扰电机,看电流变化)我们可以知道电流变化范围大概在0.01~0.1这个数量级。另一方面,我们的比较值是65536,也就是我们的比例因子如果是1000,我们测量得到的电流误差乘上1000,得到的输出的比较值变化范围大概是10-100,它大概占了65535的0.0015%~0.15%,让我们再做一个假设:PWM占空比与输出电压是线性关系,即65535输出24V电压,那么1输出0.00036V电压。聪明的你应该猜出来了,如果使用1000的比例因子,输出电压大概是0.0036V~0.036V。假设1ms对电流调节一次,那么1000mS内电机上的电流变化是1000*(0.0036~0.036)V = 3.6V~36V,这对电机的影响已经很显著了。如果比例因子是100,那么这个值是0.36V~3.6V,再缩小的话,比例因子是10,变化范围变成了0.036V~0.36V。数量级往上呢?比例因子变成10000,这个值变成:36V-360V。
上面的假设和思考过程已经告诉了我们使用纯比例调节时Kp范围:大概是100-10000这个·数量级(前提是我们测量的电流值是现实意义中的电流值而不是AD转换得到的数字)。
这个引导大家思考的过程只是一个例子。
公式化调参方法
-
PID控制器的齐格勒-尼科尔斯整定
手动调参看完了,可能大家都觉得麻烦,有没有什么公式,知道电机的一些参数,然后直接估计PID的值呢?还真有,请看下面的内容。
选择PID控制器中各个参数值的过程被称作整定。实际应用中,工程师们(也就是在座的各位,嘿嘿)往往依靠经验来整定参数,特别是化工方面的控制,经验调参为主。当然,一个经验丰富的工程师,手动调参当然可以,但是对于我们初学者来说,
往往需要一些能够公式化的东西好“套套子”。下面我介绍一下齐格勒-尼科尔斯整定方法。
注意该方法使用的前提是被控对象的参数可以通过大量实验估计出来。首先,我们的控制系统对于阶跃响应应该满足下图所示的“S型”曲线:

由此,我们可以用下面的传递函数的系统阶跃响应来近似:
这是一个延迟时间为td秒的一阶系统。上式中的各个常数可以通过系统对单位阶跃响应的响应曲线获得。做法如下:在响应曲线的拐点出做切线,切线的斜率为
切线与横轴的焦点为延迟时间
曲线终值为A的值。 我们需要计算出这两个值,后面会用到。
然后,该方法有两种具体的操作:一种叫做1/4衰减法,另外一种叫做极限灵敏度法,有的地方也称为周期震荡法或临界比例度法。接下来一一介绍。
-
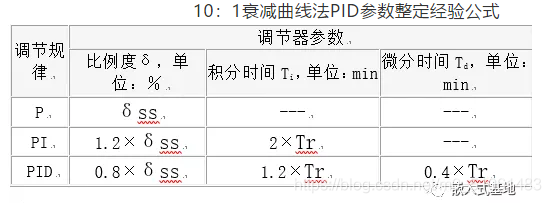
1//4衰减法
该设计方法通过改变控制器参数使闭环控制系统对单位阶跃响应的暂态响应特性衰减接近0.25。这意味着系统阶跃响应经过一个振荡周期后衰减为后来的1/4。
使用方法:
1.设定比例系数,使系统响应的第一个波峰和第二个波峰的比值接近4:1。
2.该控制器参数为:,需要自己转换为Kp,Ki,Kd形式。根据下表来选择参数,R和L的求法往回看。
| 控制器类型 | 最优增益 |
| P | Kp = 1/(RL) |
| PI | Kp = 0.9/(RL) |
| Ti = L/0.3 | |
| PID | Kp = 1.2/(RL) |
| Ti = 2L | |
| Td = 0.5 |
-
极限灵敏度法
这种方法通过改变系统参数,使得系统处于临界振荡状态,然后通过系统振荡响应的幅值和频率来估计参数值,它不是采用的阶跃响应的方法。但是该方只对开环稳定对象适用。
使用方法:
1.设定比例系数,使系统响应变成临界稳定,即系统响应类似于正弦波输出,此时称为极限增益,如下图所示,我们需要测量它的一个周期
,该周期称为极限周期。

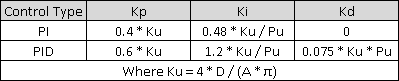
2.同样我们的控制器参数也是,根据下表选择参数计算转为Kp,Ki,Kd值。
| 控制器类型 | 最优增益 |
| P | Kp = 0.5Ku |
| PI | Kp = 0。45Ku |
| Ti = Pu/1.2 | |
| PID | Kp = 1.6Ku |
| Ti =0.5Pu | |
| Td = 0.125Pu |
实际上,我们最终整定参数时,比例增益可以使用上述值得一半,效果会好得多。
现代调参方法
-
基于误差性能指标的整定方法
-
内模整定
Matlab PID整定
Reference
参考文献
【1】SPMSM控制:传统PI电流环参数的整定 - 知乎
【2】PID控制算法精华和参数整定三大招
【3】《Feedback Control of Dynamic Systems》
【4】吴春杨. 有刷直流电机模糊PID自整定方法实验研究[D].哈尔滨工程大学,2016.
【5】Matlab仿真PID控制——衰减曲线法整定参数_FrozenC的博客-CSDN博客_衰减曲线法整定pid参数