目录
一、实验名称
二、实验目的
三、实验原理
四、实验内容及结果
五、实验收获
一、实验名称
加性高斯白噪声信道
二、实验目的
1.掌握matlab语言的基本操作和基本的编程功能;
2.掌握awgn函数和randn函数的用法;
3.了解加性高斯白噪声信道的产生方法,并学会使用awgn函数和randn函数来产生图形。
三、实验原理
1.加性高斯白噪声信道的概述
信号在信道传输的过程中,不可避免地会受到各种干扰,这些干扰统称为“噪声”。加性高斯白噪声(Additive White Gaussian Noise, AWGN)是最常见的一种噪声,它存在于各种传输媒质中,包括有线信道和无线信道。加性高斯白噪声表现为信号围绕平均值的一种随机波动过程。加性高斯白噪声的均值为0,方差是噪声功率的大小。一般情况下,噪声功率越大,信号的波动幅度就越大,接收端接收到的信号的误比特率就越高。在研究通信系统的误码率与信道质量的关系时,一般先研究它在AWGN信道下的性能,然后再把它推广到具有快衰落的复杂情况。
2. MATLAB提供了awgn函数来实现在输入信号中叠加一定强度的高斯白噪声信号,噪声信号的强度由输入参数确定。它主要有以下几种形式。
(1)awgn(x,snr)
函数awgn(x,sm)把加性高斯白噪声叠加到输入信号x中,snr以dB的形式指定噪声的功率。在这种情况下,信号x的功率假设为0dBW,因此,噪声的功率实际上就等于-snr dBW。如果x是复数,那么awgn将添加复数噪声。(2)awgn(x,snr,sigpower)
这种方法与(1)不同的是,假设了输入信号的功率为sigpower。
(3)首先计算输入信号x的功率,然后按照snr添加相应功率的高斯白噪声。
3.randn函数
randn函数也可以用来产生加性高斯白噪声,在第3章中已经用到过该函数。
(1)randn(n)
randn(n)返还一个n行n列的随机矩阵,其中每一行和每一列都服从均值为0、方差为1的正态分布。
(2)randn(m,n)
randn(m.n)返还一个m行n列的随机矩阵,其中每一行和每一列都服从均值为0、方差为1的正态分布。
(3)randn('state',seed)
randn(stateseed)把随机数种子设定为seed,相同的state产生相同的随机数序列。
四、实验内容及结果
编制程序使用awgn函数和randn函数实现对加性高斯白噪声信号进行功率叠加、改变信号功率、计算噪声功率和方差,并对所有结果做一个对比和分析。
(一)实验一:在正弦信号上叠加功率为-20dBW的高斯白噪声。
1.实验代码
%加性高斯白噪声信道-用awgn(x,snr)实现t=0:0.001:10; %产生时间矢量tx=sin(2*pi*t); %生成正弦信号xsnr=20; %设定加性高斯白噪声的功率snry=awgn(x,snr); %在正弦信号上叠加高斯白噪声z=y-x; %计算噪声功率f=var(z); %计算噪声方差subplot(2,2,1); %定义第一个图像plot(t,x,'g-'); %画出原始信号title('正弦信号x'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('x=sin(2Πt)'); %对纵轴进行说明subplot(2,2,2); %定义第二个图像plot(t,y,'r-'); %画出叠加了噪声后的信号title('叠加了高斯白噪声后的正弦信号y'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('y=awgn(x,snr)'); %对纵轴进行说明subplot(2,2,3); %定义第三个图像plot(t,z,'b-'); %画出噪声功率的信号title('噪声功率'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('z=y-x'); %对纵轴进行说明subplot(2,2,4); %定义第四个图像plot(t,f,'k.'); %画出噪声方差的信号title('噪声方差'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('f=var(z)'); %对纵轴进行说明2.实验结果
计算出的噪声功率为ans=0.0100。
说明:程序第2行是产生时间矢量,第3行是生成正弦信号,第4行是设定加性高斯白噪声的功率,第5行是在正弦信号上叠加高斯白噪声,第6~7行是画出原始信号和叠加了噪声后的信号,第9~10行是计算噪声的功率(方差)。
从上图可以看出,叠加了噪声后的信号与原信号相比有了失真,并且计算出的噪声功
率为0.01,而且这个功率是由snr决定的。(二)实验二:现在设实验一中的信号功率为10dBW,snr保持不变,再重新求解。
1.实验代码
%加性高斯白噪声信道-用awgn(x,snr,'measured')实现t=0:0.001:10; %产生时间矢量tx=sin(2*pi*t); %生成正弦信号xsnr=20; %设定加性高斯白噪声的功率snry=awgn(x,snr,'measured'); %在正弦信号上叠加高斯白噪声z=y-x; %计算噪声功率f=var(z); %计算噪声方差subplot(2,2,1); %定义第一个图像plot(t,x,'g-'); %画出原始信号title('正弦信号x'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('x=sin(2Πt)'); %对纵轴进行说明subplot(2,2,2); %定义第二个图像plot(t,y,'r-'); %画出叠加了噪声后的信号title('叠加了高斯白噪声后的正弦信号y'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('y=awgn(x,snr,‘measured’)'); %对纵轴进行说明subplot(2,2,3); %定义第三个图像plot(t,z,'b-'); %画出噪声功率的信号title('噪声功率'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('z=y-x'); %对纵轴进行说明subplot(2,2,4); %定义第四个图像plot(t,f,'m.'); %画出噪声方差的信号title('噪声方差'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('f=var(z)'); %对纵轴进行说明2.实验结果2.实验结果
计算出的噪声功率为0.100。
比较图实验一与实验二的结果可以明显看出,实验二的结果的失真要远大于实验一的结果,这是因为输入信号的功率实际上小于10dBW,因此,虽然snr保持不变,但噪声功率实际上增大了,从计算出的噪声功率上也证明了这一点。
(三)实验三:计算实验一中输入信号的功率,根据snr添加高斯白噪声。
1.实验代码
%加性高斯白噪声信道-用awgn(x,snr,'measured')实现t=0:0.001:10; %产生时间矢量tx=sin(2*pi*t); %生成正弦信号xsnr=20; %设定加性高斯白噪声的功率snry=awgn(x,snr,'measured'); %在正弦信号上叠加高斯白噪声z=y-x; %计算噪声功率f=var(z); %计算噪声方差subplot(2,2,1); %定义第一个图像plot(t,x,'g-'); %画出原始信号title('正弦信号x'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('x=sin(2Πt)'); %对纵轴进行说明subplot(2,2,2); %定义第二个图像plot(t,y,'r-'); %画出叠加了噪声后的信号title('叠加了高斯白噪声后的正弦信号y'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('y=awgn(x,snr,‘measured’)'); %对纵轴进行说明subplot(2,2,3); %定义第三个图像plot(t,z,'b-'); %画出噪声功率的信号title('噪声功率'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('z=y-x'); %对纵轴进行说明subplot(2,2,4); %定义第四个图像plot(t,f,'m.'); %画出噪声方差的信号title('噪声方差'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('f=var(z)'); %对纵轴进行说明2.实验结果

计算出的噪声功率为0.005。
从本实验的结果图可以看出,添加噪声后的信号失真要小于实验一和实验二,这是因为添加的噪声功率根据实际的信号功率计算得到,而实际的信号的功率为0.5,因此,添加的噪声功率为0.005,与计算结果一致,并且要小于实验一和实验二的噪声功率。
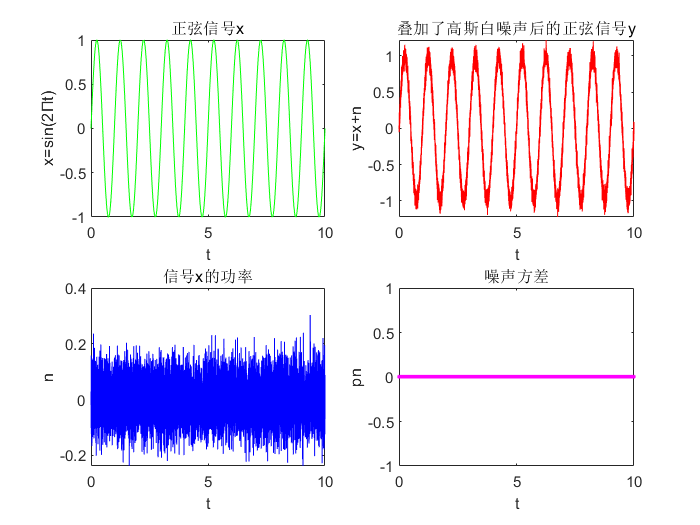
(四)实验四:用randn函数实现实验三。
1.实验代码
%加性高斯白噪声信道-用randn函数实现t=0:0.001:10; %产生时间矢量tx=sin(2*pi*t); %生成正弦信号xsnr=20; %设定加性高斯白噪声的功率snrpx=norm(x).^2/length(x); %计算信号x的功率pn=px./(10.^(snr./10)); %根据snr计算噪声功率n=sqrt(pn)*randn(1,length(x)); %根据噪声功率产生相应的高斯白噪声序列y=x+n; %在信号上叠加高斯白噪声subplot(2,2,1); %定义第一个图像plot(t,x,'g-'); %画出原始信号title('正弦信号x'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('x=sin(2Πt)'); %对纵轴进行说明subplot(2,2,2); %定义第二个图像plot(t,y,'r-'); %画出叠加了噪声后的信号title('叠加了高斯白噪声后的正弦信号y'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('y=x+n'); %对纵轴进行说明subplot(2,2,3); %定义第三个图像plot(t,n,'b-'); %画出噪声功率产生相应的高斯白噪声序列title('信号x的功率'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('n'); %对纵轴进行说明subplot(2,2,4); %定义第四个图像plot(t,pn,'m.'); %画出噪声功率title('噪声方差'); %对图像主题的说明xlabel('t'); %对横轴进行说明ylabel('pn'); %对纵轴进行说明2.实验结果
计算出的噪声功率为0.005。
比较本实验和实验三可以看出,两者的效果是一样的。最后计算出的噪声功率也证明了这一点。
除了randn函数外,MATLAB还提供了wgn函数,也可以用来产生高斯白噪声;此外,rand函数用来产生在[0.1]上服从均匀分布的白噪声,要与randn函数区别开来。它们的用法分别与awgn函数和randn函数类似,我们可以参考MATLAB帮助手册。
五、实验收获
通过本次实验,对awgn函数、randn函数、var函数、norm函数、length函数、sqrt函数有了一定的了解,学会了他们的用法,并对高斯白噪声信号有了一定的认识。
总之,只要积极主动、细心、有耐心,注意理论联系实际、多做多学多问,就会有进步,就会学到更多知识。