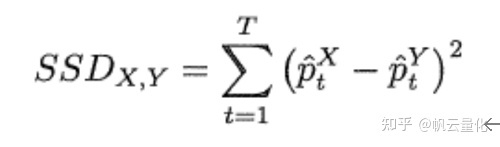点赞、关注再看,养成良好习惯
Life is short, U need Python
初学量化投资实战,[快来点我吧]
配对交易策略实战—最短距离法
基本流程
配对组合 --> 计算价差 --> 决策标准 --> 确定头寸 --> 平仓获利
一、股票对的选取
- 读取数据
import pandas as pdsh = pd.read_csv('sh50_stock_data.csv',index_col='Trddt') # 读取上证板块收盘价数据
- 数据预处理
# 将stock转换成时间序列类型
sh.index = pd.to_datetime(sh.index)
# 定义配对形成期
formStart = '2014-01-01'
formEnd = '2015-01-01'
# 形成期数据
sh_form = sh[formStart:formEnd]
sh_form.head()
| 600000 | 600010 | 600015 | 600016 | 600018 | 600028 | 600030 | 600036 | 600048 | 600050 | ... | 601688 | 601766 | 601800 | 601818 | 601857 | 601901 | 601985 | 601988 | 601989 | 601998 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Trddt | |||||||||||||||||||||
| 2014-01-02 | 8.307 | 2.360 | 6.371 | 6.183 | 5.031 | 4.117 | 12.288 | 9.719 | 5.156 | 3.146 | ... | 8.534 | 4.869 | 3.781 | 2.383 | 7.245 | 5.91 | - | 2.333 | 5.617 | 3.634 |
| 2014-01-03 | 8.138 | 2.594 | 6.187 | 6.087 | 4.906 | 4.043 | 11.937 | 9.520 | 5.112 | 3.088 | ... | 8.293 | 4.791 | 3.725 | 2.356 | 7.217 | 5.91 | - | 2.289 | 5.517 | 3.578 |
| 2014-01-06 | 8.182 | 2.439 | 6.041 | 5.911 | 4.581 | 4.136 | 11.937 | 9.475 | 4.822 | 3.000 | ... | 8.438 | 4.606 | 3.63 | 2.32 | 7.339 | 5.91 | - | 2.262 | 5.198 | 3.521 |
| 2014-01-07 | 8.138 | 2.380 | 6.018 | 5.847 | 4.945 | 4.062 | 11.751 | 9.529 | 4.778 | 3.010 | ... | 8.331 | 4.538 | 3.659 | 2.32 | 7.311 | 5.91 | - | 2.253 | 5.148 | 3.512 |
| 2014-01-08 | 8.191 | 2.295 | 6.149 | 5.863 | 4.706 | 4.052 | 11.791 | 9.629 | 4.734 | 2.971 | ... | 8.36 | 4.441 | 3.64 | 2.32 | 7.217 | 5.91 | - | 2.244 | 5.138 | 3.521 |
5 rows × 50 columns
结论:发现有空缺值(标记为‘-’)。
sh_form = sh_form.drop(['600958','601211','601985'], axis=1) # 删除空缺值
sh_form = sh_form.astype(float) # 转换为浮点值
# 提取中国银行(601988)A和浦发银行(600000)B股票的调整后的收盘价格数据
P_zhonghang_f = sh_form['601988']
P_pufa_f = sh_form['600000']
# 合并数据形成DataFrame数据
pair_form = pd.concat([P_zhonghang_f,P_pufa_f],axis =1,join='outer')
- 数据可视化
# 股票对价格历史走势图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] plt.figure(figsize=(10,4))
ax = plt.subplot()ax.plot(pair_form['601988'], label='中国银行')
ax.plot(pair_form['600000'], label='浦发银行')
plt.title('图1 中国银行 vs 浦发银行(收盘价)',fontsize=15)
ax.set_xlabel('日期', fontsize=14)
ax.set_ylabel('收盘价', fontsize=14)
ax.legend()plt.show()
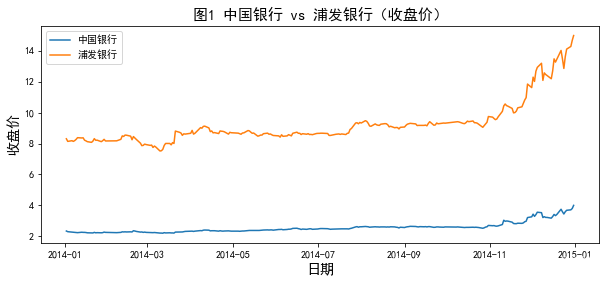
# 计算 A、B 收益率
return_zhonghang = (P_zhonghang_f - P_zhonghang_f.shift(1)) / P_zhonghang_f.shift(1)[1:]
return_pufa = (P_pufa_f - P_pufa_f.shift(1)) /P_pufa_f.shift(1)[1:]
# 股票对价格历史走势图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei']
import matplotlib
matplotlib.rcParams['axes.unicode_minus']=False # 负号显示问题plt.figure(figsize=(10,4))
ax = plt.subplot()ax.plot(return_zhonghang, label='中国银行')
ax.plot(return_pufa, label='浦发银行')
plt.title('图2 中国银行 vs 浦发银行(收益率)',fontsize=15)
ax.set_xlabel('日期', fontsize=14)
ax.set_ylabel('收益率', fontsize=14)
ax.legend()plt.show()
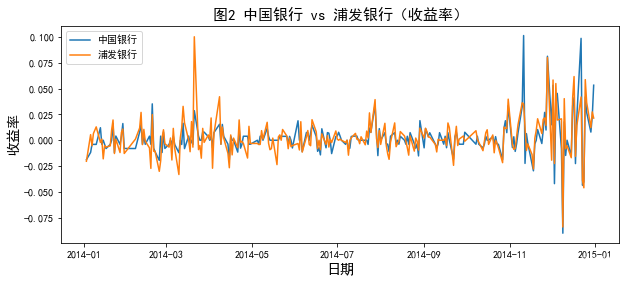
# 计算 A、B 累计收益率
cum_return_zhonghang = (1 + return_zhonghang).cumprod()
cum_return_pufa = (1 + return_pufa).cumprod()
# 股票对累计收益率历史走势图
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] plt.figure(figsize=(10,4))
ax = plt.subplot()ax.plot(cum_return_zhonghang, label='中国银行')
ax.plot(cum_return_pufa, label='浦发银行')
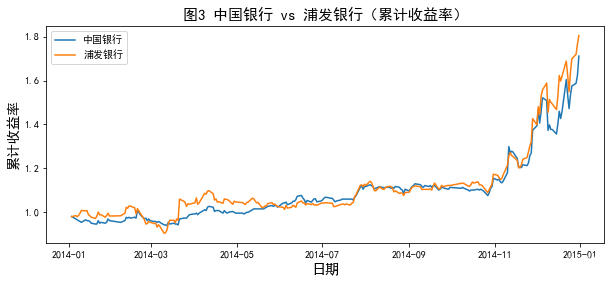
plt.title('图3 中国银行 vs 浦发银行(累计收益率)',fontsize=15)
ax.set_xlabel('日期', fontsize=14)
ax.set_ylabel('累计收益率', fontsize=14)
ax.legend()plt.show()
- 构造最小距离函数–SSD()
## 构造SSD距离函数(累计收益率偏差)
import numpy as npdef SSD(priceX,priceY): returnX = (priceX - priceX.shift(1)) / priceX.shift(1)[1:] # 计算 X 收益率returnY = (priceY - priceY.shift(1)) / priceY.shift(1)[1:] # 计算 Y 收益率standardX = (returnX + 1).cumprod() # 累计求和‘.cumprod()’,即 X,Y 的累计收益率standardY = (returnY + 1).cumprod()SSD = np.sum((standardX - standardY) ** 2) # 计算累计收益率偏差return(SSD)
# 求中国银行和浦发银行价格距离
dis = SSD(P_zhonghang_f,P_pufa_f)
dis
0.47481704588389073
结论:
将上证50板块的50只股票两两配对(共计1225对),形成期(Formation Period)为245天,则 X X X、 Y Y Y股票的价格距离为:
S S D X , Y = ∑ t = 1 245 ( p ^ t X − p ^ t Y ) 2 SSD_{X, Y}=\sum_{t=1}^{245}\left(\hat{p}_{t}^{X}-\hat{p}_{t}^{Y}\right)^{2} SSDX,Y=t=1∑245(p^tX−p^tY)2
以此类推,可以计算出1225个SSD值,将这些值由小到大进行排序,然后从中选出前5组作为配对交易策略的5个股票对。
- 计算上证50板块两两配对股票(1225 --》1081对)之间的距离
lst = list(sh_form.columns)
d = dict()
for i in range(len(lst)):for j in range(i+1,len(lst)):P_zhonghang_f = sh_form[lst[i]]P_pufa_f = sh_form[lst[j]]dis = SSD(P_zhonghang_f,P_pufa_f)d[lst[i]+'-'+lst[j]] = dis
# 按照‘值’排序,并挑出前5个最小距离股票对
d_sort = sorted(d.items(),key=lambda x:x[1])
d_sort[:5]
[('600015-601166', 0.24566159437495438),('601288-601398', 0.246846282979896),('600050-601288', 0.27890721330378976),('601166-601288', 0.2920160356208131),('601398-601857', 0.3299872459845748)]
二、配对交易策略的制定
运用最小距离法可以挑选出股票对,计算形成期(Formation Period)内标准化的价格序列差 p ^ t X − p ^ t Y \hat{p}_t^X - \hat{p}_t^Y p^tX−p^tY 的平均值 μ \mu μ 和标准差 σ \sigma σ。然后,选定交易期(Trading Period )进行交易。
Gatev等学者运用最小距离法选出股票对,设定交易信号触发点为 μ ± 2 σ \mu \pm 2\sigma μ±2σ,交易期的适用期限为6个月。当交易期超过6个月以后,重新设定形成期和选取股票对。此处,由于浦发银行与中国银行同为银行业股票,且银行业股票股价比较稳定,因此我们设定交易期内价差超过 μ + 1.2 σ \mu + 1.2\sigma μ+1.2σ 或者 μ − 1.2 σ \mu - 1.2\sigma μ−1.2σ 时,将触发交易信号进行交易。
当交易期的标准化价差又回复到均值 μ \mu μ 附近时,反向操作平仓,从而赚取价差收益。
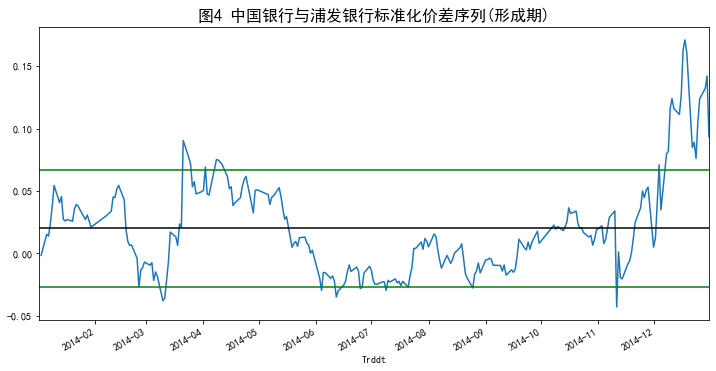
- (1)在形成期中计算浦发银行与中国银行股票标准化价格序列差
SSD-pair,并求出价差的平均值meanSSD-pair和标准差sdSSD-pair,并设定开仓、平仓条件(如图4所示)。
# 中国银行标准化价格
standard_zhonghang = (1 + return_zhonghang).cumprod()
# 浦发银行标准化价格
standard_pufa = (1 + return_pufa).cumprod()
# 求中国银行A与浦发银行B标准化价格序列的价差
SSD_pair = standard_pufa - standard_zhonghang
############ (1.1)计算形成期标准化价格差序列的均值和方差 ############
meanSSD_pair = np.mean(SSD_pair)
sdSSD_pair = np.std(SSD_pair)
############ (1.2)设置交易期交易信号触发点:mu +- 1.2sigma ############
thresholdUp = meanSSD_pair + 1.2 * sdSSD_pair
thresholdDown = meanSSD_pair - 1.2 * sdSSD_pair
# 可视化
plt.figure(figsize=(12,6))SSD_pair.plot()plt.title('图4 中国银行与浦发银行标准化价差序列(形成期)',loc='center',fontsize=16) plt.axhline(y=meanSSD_pair,color='black')
plt.axhline(y=thresholdUp,color='green')
plt.axhline(y=thresholdDown,color='green') plt.show()
- (2)设定交易期(Trading Period )时间,选取交易期数据,寻找配对交易开仓和平仓位点。当价差上穿 μ + 1.2 σ \mu + 1.2\sigma μ+1.2σ 线时,反向开仓,当价差线回复到均线附近(可以给出阈值进行度量)时,进行平仓。当价差线下穿 μ − 1.2 σ \mu - 1.2\sigma μ−1.2σ 线时正向开仓,当价差线再次回复到均线附近时平仓。
################### 设定交易期时间,选取交易期数据,寻找配对交易开仓和平仓点位(2.1) ###################
tradStart = '2015-01-01'
tradEnd = '2015-06-30'
P_zhonghang_t = sh.loc[tradStart:tradEnd, '601988']
P_pufa_t = sh.loc[tradStart:tradEnd, '600000']
# 定义价差函数
def spreadCal(x,y):retx = (x-x.shift(1)) / x.shift(1)[1:]rety = (y-y.shift(1)) / y.shift(1)[1:]standardX = (1+retx).cumprod()standardY = (1+rety).cumprod()spread = standardX-standardYreturn(spread)
# 计算标准价差
TradSpread = spreadCal(P_pufa_t,P_zhonghang_t).dropna()
# 可视化
plt.figure(figsize=(12,6))TradSpread.plot()plt.title('图5 中国银行与浦发银行股票价差序列(交易期)',loc='center',fontsize=16)plt.axhline(y=meanSSD_pair, color='black')
plt.axhline(y=thresholdUp, color='green')
plt.axhline(y=thresholdDown, color='green') plt.show()
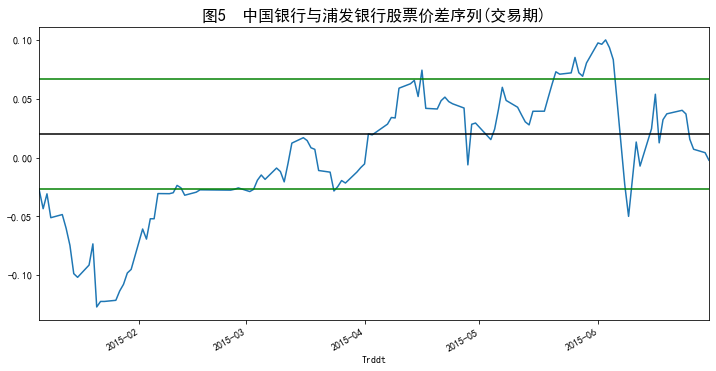
结论:如图5所示,价差序列多在1.2倍标准差范围内,从2015年1月1日至2015年6月30日,价差序列向上突破1.2倍标准差线3次,向下突破1.2倍标准差线3次,共有6次开仓机会,且价差序列比较稳定,开仓后均有平仓机会。
注:(1)均值附近平仓的度量: μ ± 0.2 σ \mu \pm 0.2\sigma μ±0.2σ;(2)控制风险平仓的度量: μ ± 2.0 σ \mu \pm 2.0\sigma μ±2.0σ。
三、构建PairTrading类
Python是一种面向对象的语言,我们可以构建各种各样的类来完成我们所需要的任务。对于上文中进行配对的代码,我们可以将其编写为一个类。这样,在以后需要的时候,就可以随时调用该类,而不需要再重新编写上面的那些代码。
import pandas as pd
import numpy as np from arch.unitroot import ADF
import statsmodels.api as sm
# 构建类
class PairTrading:def SSD(self,priceX,priceY):returnX = (priceX - priceX.shift(1)) / priceX.shift(1)[1:]returnY = (priceY - priceY.shift(1)) / priceY.shift(1)[1:]standardX = (returnX + 1).cumprod()standardY = (returnY + 1).cumprod()SSD = np.sum((standardY - standardX)**2)return(SSD)def SSD_Spread(self,priceX,priceY):priceX = np.log(priceX)priceY = np.log(priceY)retx = priceX.diff()[1:]rety = priceY.diff()[1:]standardX = (1 + retx).cumprod()standardY = (1 + rety).cumprod()spread = standardY - standardXreturn(spread)def SSD_Cal_Bound(self,priceX,priceY,width=1.5):spread = self.SSD_Spread(priceX,priceY) mu = np.mean(spread)sd = np.std(spread)UpperBound = mu + width * sdLowerBound = mu - width * sdreturn(UpperBound,LowerBound)
- 现在调用上述构建的类PairTrading,来快速计算中国银行与浦发银行的最小距离、价差序列以及交易期价差的阈值。
# 读入数据
sh = pd.read_csv('sh50_stock_data.csv',index_col='Trddt')
sh.index = pd.to_datetime(sh.index)
# 选取标的
price_zhonghang = sh['601988']
price_pufa = sh['600000']
# 形成期价格
price_zhonghang_form = price_zhonghang[formStart:formEnd]
price_pufa_form = price_pufa[formStart:formEnd]# 交易期价格
price_zhonghang_trade = price_zhonghang[tradStart:tradEnd]
price_pufa_trade = price_pufa[tradStart:tradEnd]
# 类的实例化
pt = PairTrading() # 调用类PairTrading()
# 计算SSD
SSD = pt.SSD(price_zhonghang_form,price_pufa_form)
SSD
0.47481704588389073
# 形成期:SSDspread(价差序列)
SSDspread = pt.SSD_Spread(price_zhonghang_form,price_pufa_form)
# 根据形成期协整配对后价差序列得到的阈值1(开仓)
bound_1 = pt.SSD_Cal_Bound(price_zhonghang,price_pufa,width=1.2)
bound_1
(0.07135801363557201, -0.1252480116392951)
# 根据形成期协整配对后价差序列得到的阈值2(平仓)
bound_2 = pt.SSD_Cal_Bound(price_zhonghang,price_pufa,width=0.2)
bound_2
(-0.010561163562289283, -0.04332883444143381)
# 根据形成期协整配对后价差序列得到的阈值3(止损)
bound_3 = pt.SSD_Cal_Bound(price_zhonghang,price_pufa,width=2.0)
bound_3
(0.13689335539386108, -0.19078335339758415)
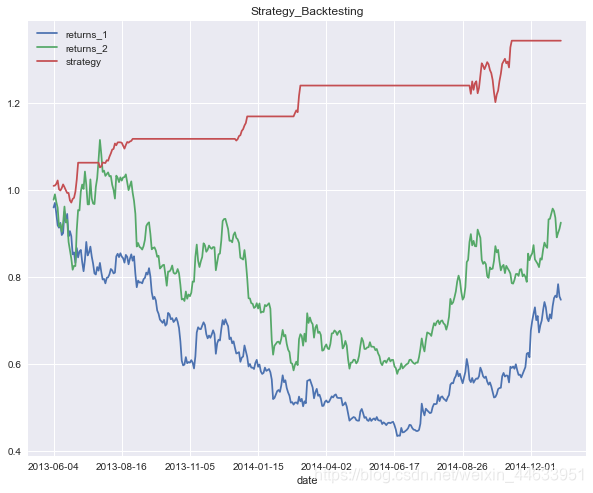
四、配对交易策略的回测(实测)
接下来,运用中国银行和浦发银行股票的交易数据自行设计配对交易策略,这一次将2014年1月1日到2014年12月31日作为配对形成期,以及将2015年1月
1日到2015年6月30日作为交易期。用Python实现配对交易策略大致有如下4个步骤。
- (1) 在形成期内,计算中国银行和浦发银行两只股票价差序列的平均值( μ \mu μ)和标准差( σ \sigma σ)。
- (2) 在交易期内,设定 μ \mu μ ± \pm ± 1.5 σ 1.5\sigma 1.5σ 为开仓阈值、 μ ± 0.2 σ \mu \pm 0.2\sigma μ±0.2σ 为平仓阈值,将 μ ± 2.5 σ \mu \pm 2.5\sigma μ±2.5σ 为止损阈值,具体交易规则如下:
- 当价差上穿 μ + 1.5 σ \mu + 1.5\sigma μ+1.5σ 时,做空配对股票,反向建仓(即卖出浦发银行,买入中国银行,二者资金比值为 β \beta β);
- 当价差下穿 μ + 0.2 σ \mu + 0.2\sigma μ+0.2σ 时,反向平仓;
- 当价差下穿 μ − 1.5 σ \mu - 1.5\sigma μ−1.5σ 时,做多配对股票,正向建仓(即买入浦发银行,卖出中国银行,二者资金比值为 β \beta β);
- 当价差上穿 μ − 0.2 σ \mu - 0.2\sigma μ−0.2σ 时,正向平仓;
- 当价差突破 μ ± 2.5 σ \mu \pm 2.5\sigma μ±2.5σ 时,及时止损。
- (3) 配对交易策略绩效评价
接下来用Python编写代码,对浦发银行和中国银行股票进行从头到尾的配对交易策略实测。
- (1) 获取数据,在形成期内,计算中国银行和浦发银行两只股票价差序列的平均值( μ \mu μ)和标准差( σ \sigma σ)。
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif'] = ['SimHei'] from arch.unitroot import ADF
import statsmodels.api as sm
# 读取数据
sh = pd.read_csv('sh50_stock_data.csv',index_col='Trddt')
sh.index = pd.to_datetime(sh.index)
# 形成期:提取数据
P_zhonghang = sh['601988']
P_pufa = sh['600000']price_zhonghang_form = P_zhonghang[formStart:formEnd]
price_pufa_form = P_pufa[formStart:formEnd]
# 类的实例化
pt = PairTrading() # 调用类PairTrading()# 形成期:SSDspread(价差序列)
SSD_spread_form = pt.SSD_Spread(price_zhonghang_form,price_pufa_form)
# 计算均值、方差
mu = np.mean(SSD_spread_form)
sd = np.std(SSD_spread_form)
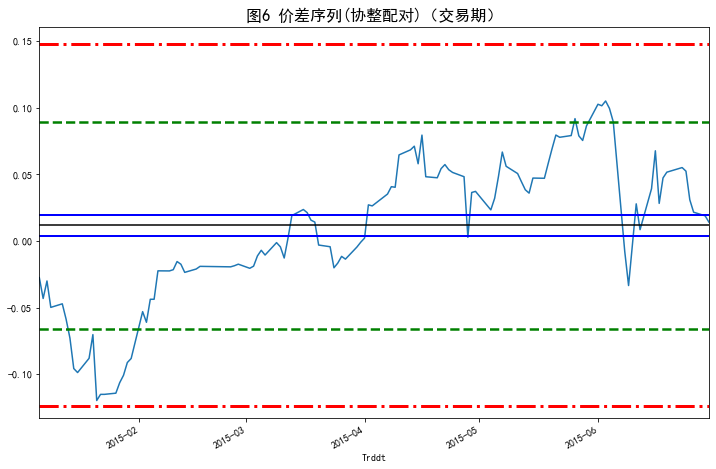
- (2) 选取交易期价格数据,构造开仓平仓区间(如图6所示)。
# 提取交易期数据
price_zhonghang_trade = P_zhonghang[tradeStart:tradEnd]
price_pufa_trade = P_pufa[tradeStart:tradEnd]
# 交易期:SSDspread(价差序列)
SSD_spread_trade = pt.SSD_Spread(price_zhonghang_trade,price_pufa_trade)
# 绘制价格区间图
plt.figure(figsize=(12,8))SSD_spread_trade.plot()plt.title('图6 价差序列(协整配对)(交易期)',loc='center', fontsize=16)plt.axhline(y=mu,color='black')
plt.axhline(y=mu+0.2*sd,color='blue',ls='-',lw=2)
plt.axhline(y=mu-0.2*sd,color='blue',ls='-',lw=2)
plt.axhline(y=mu+2.0*sd,color='green',ls='--',lw=2.5)
plt.axhline(y=mu-2.0*sd,color='green',ls='--',lw=2.5)
plt.axhline(y=mu+3.5*sd,color='red',ls='-.',lw=3)
plt.axhline(y=mu-3.5*sd,color='red',ls='-.',lw=3) plt.show()
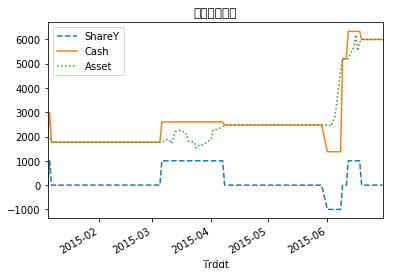
- (4) 根据开仓平仓点制定交易策略,并模拟交易账户(如图7所示)。
# 设置信号触发点
level = (float('-inf'),mu-3.5*sd,mu-2.0*sd,mu-0.2*sd,mu+0.2*sd,mu+2.0*sd,mu+3.5*sd,float('inf'))
prcLevel = pd.cut(SSD_spread_trade,level,labels=False) - 3 #剪切函数pd.cut()
- 构造交易信号函数(以上述levels为例)
# 构造交易信号函数
def TradeSig(prcLevel):n = len(prcLevel)signal = np.zeros(n)for i in range(1,n):if prcLevel[i-1] == 1 and prcLevel[i] == 2: #价差从1区上穿2区,反向建仓signal[i] = -2elif prcLevel[i-1] == 1 and prcLevel[i] == 0: #价差从1区下穿0区,平仓signal[i] = 2elif prcLevel[i-1] == 2 and prcLevel[i] == 3: #价差从2区上穿3区,即突破3区,平仓signal[i] = 3elif prcLevel[i-1] == -1 and prcLevel[i] == -2: #价差从-1区下穿-2区,正向建仓signal[i] = 1elif prcLevel[i-1] == -1 and prcLevel[i] == 0: #价差从-1区上穿0区,平仓signal[i] = -1elif prcLevel[i-1] == -2 and prcLevel[i] == -3: #价差从-2区下穿-3区,即突破-3区,平仓signal[i] = -3return(signal)
signal = TradeSig(prcLevel)
# 设置买卖条件(信号)
position = [signal[0]]
ns = len(signal)for i in range(1,ns):position.append(position[-1])if signal[i] == 1:position[i] = 1elif signal[i] == -2:position[i] = -1elif signal[i] == -1 and position[i-1] == 1:position[i] = 0elif signal[i] == 2 and position[i-1] == -1:position[i] = 0elif signal[i] == 3:position[i] = 0elif signal[i] == -3:position[i]=0
# 计算交易信号
position = pd.Series(position, index=SSD_spread_trade.index)
# 构造交易模拟函数
def TradeSim(priceX,priceY,position):n = len(position)size = 1000beta = 1 # 确定交易头寸:等权重;delta对冲;资金比例shareY = size * positionshareX = [(-beta) * shareY[0] * priceY[0] / priceX[0]]cash = [2000] # 1000股浦发大概15000元左右,10%保障金大概1500元!所以,取2000元初始金!!for i in range(1,n):shareX.append(shareX[i-1])cash.append(cash[i-1])if position[i-1] == 0 and position[i] == 1:shareX[i] = (-beta) * shareY[i] * priceY[i] / priceX[i]cash[i] = cash[i-1] - (shareY[i] * priceY[i] + shareX[i] * priceX[i])elif position[i-1] == 0 and position[i ]== -1:shareX[i] = (-beta) * shareY[i] * priceY[i] / priceX[i]cash[i] = cash[i-1] - (shareY[i] * priceY[i] + shareX[i] * priceX[i])elif position[i-1] == 1 and position[i] == 0:shareX[i] = 0cash[i] = cash[i-1] + (shareY[i-1] * priceY[i] + shareX[i-1] * priceX[i])elif position[i-1] == -1 and position[i] == 0:shareX[i] = 0cash[i] = cash[i-1] + (shareY[i-1] * priceY[i] + shareX[i-1] * priceX[i])cash = pd.Series(cash,index=position.index)shareY = pd.Series(shareY,index=position.index)shareX = pd.Series(shareX,index=position.index)asset = cash + shareY * priceY + shareX * priceXaccount = pd.DataFrame({'Position':position,'ShareY':shareY,'ShareX':shareX,'Cash':cash,'Asset':asset})return(account)
account = TradeSim(price_zhonghang_trade,price_pufa_trade,position)
account.iloc[:, [1,2,3,4]].plot(style=['--','--','-',':'], color=['red','blue','yellow','green'],figsize=(16,8))plt.title('图7 配对交易账户',loc='center', fontsize=16) plt.show()
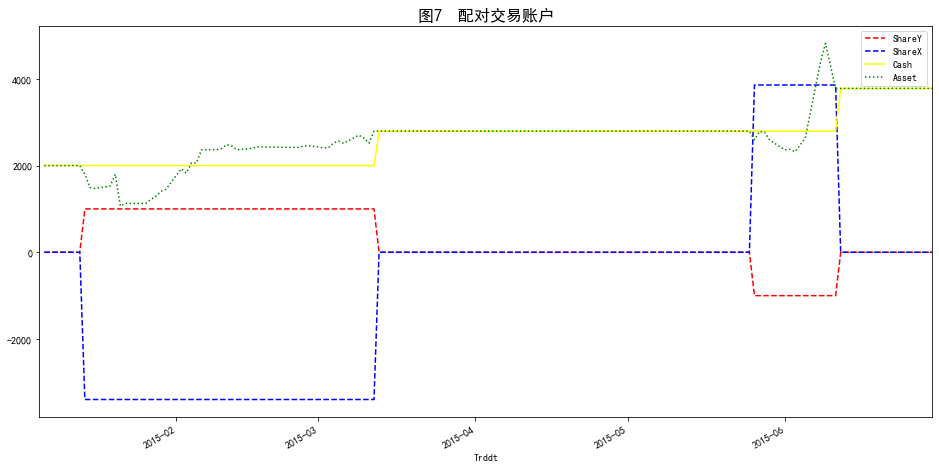
- ShareX、ShareY单位:股数(正代表买入,负代表卖出)
- Cash、Asset单位:元
参考资料:
- 蔡立耑. 量化投资以Python为工具[M]. 北京:电子工业出版社,2017.
数据下载
- 请在留言区留下您的邮箱(其实任何其他标的的数据都可以替代)!
- 写作不易,切勿白剽
- 博友们的点赞和关注就是对博主坚持写作的最大鼓励
- 持续更新,未完待续…