目录
一、概念
二、操作说明
1.树与图的深度优先遍历
2.树的DFS序
3.树的深度
4.树的重心
5.图的连通块划分
三、例题实践
1.树的重心例题实战
a.题目描述
b.解题思路
c.代码实现
一、概念
树与图的深度优先遍历:深度优先遍历,就是在每一个点x上面对多条分支时,任选一条边走下去,执行递归,直至回溯到点x后,再考虑其他的边。
树的DFS序:在对树进行深度优先遍历时,对于每一个节点,在刚进入递归后以及即将回溯前各记录一次该点的编号,最后产生的长度为2N的节点序列就被称为树的DFS序。
树的深度:树中的各个节点的深度是一种自顶向下的统计信息,大小为由节点到到根节点的距离。
树的重心:在删除一个节点后,一棵树可能会产生多个子树,其中能使产生子树的最大值最小的节点,就被称为整棵树的重心。
图的连通块:若在无向图的一个子图中,任意两个节点之间都存在一条路径(可相互到达),且该子图是不能再扩张的,则称该子图为无向图的一个连通块。
注:树与图最常见的存储方式就是使用一个邻接表保存它们的边集
二、操作说明
1.树与图的深度优先遍历
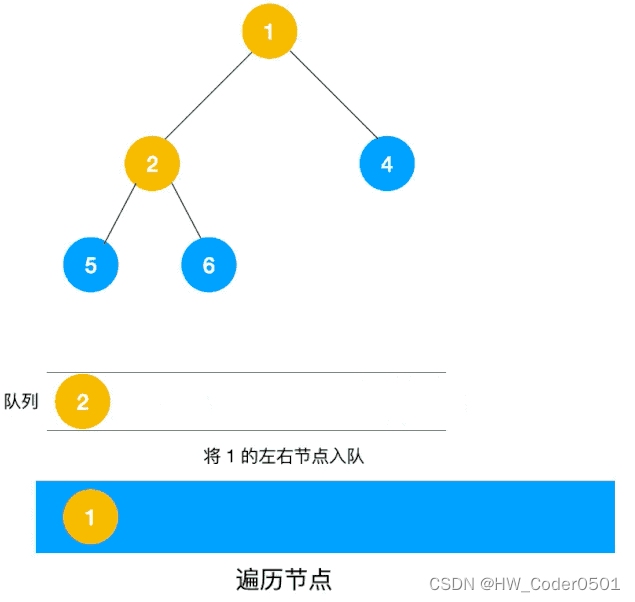
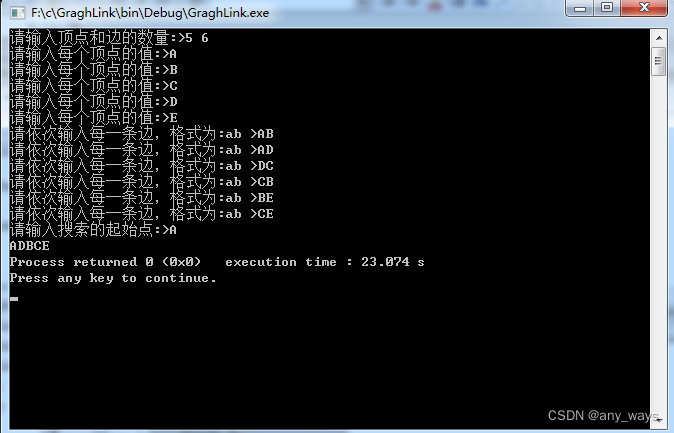
遍历形式如图1所示
int h[N],e[M],ne[M],idx; ///邻接表结构
bool st[N];void dfs(int u){st[u]=true; ///标记已遍历过的点for(int i=h[u];i!=-1;i=ne[i]){ ///遍历与点u相连的点int j=e[i]; ///将与点u相连的点存入jif(!st[j]) dfs(j); ///若点j未被遍历过,则对与点j相连的点进行搜索}}2.树的DFS序
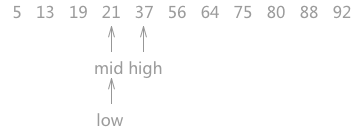
DFS序的特点是:每个节点的编号在序列中恰好出现两次。设这两次出现的位置为L[x]和R[x],那么闭区间[L[x],R[x]]就是以x为根的子树的DFS序。样例如图2
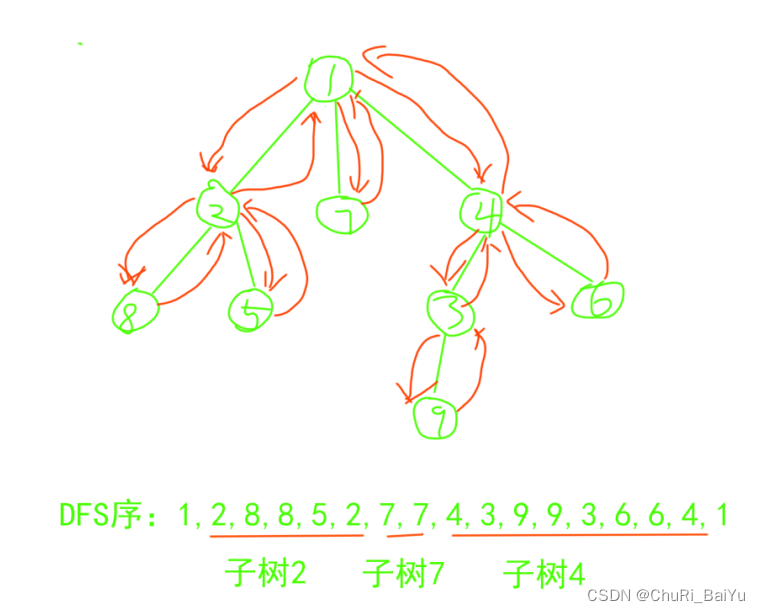
void dfs(int u){a[++m]=u; ///a数组存储DFS序st[u]=true;for(int i=h[u];i!=-1;i=ne[i]){int j=e[i];if(!st[j]) dfs(j);}a[++m]=u;
}3.树的深度
树的根节点深度为0。若结点u的深度为d[u],则它的子节点j深度为d[j]=d[u]+1。样例如图3所示。
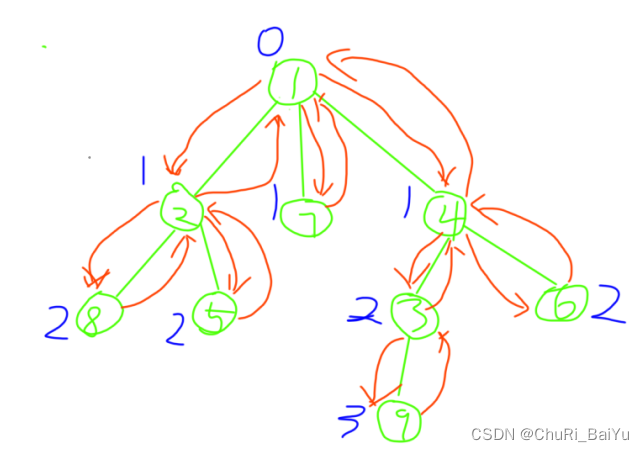
void dfs(int u){st[u]=true;for(int i=h[u];i!=-1;i=ne[i]){int j=e[i];if(!st[j]) {d[j]=d[u]+1; ///子节点的深度等于父节点加1dfs(j);}}
}4.树的重心
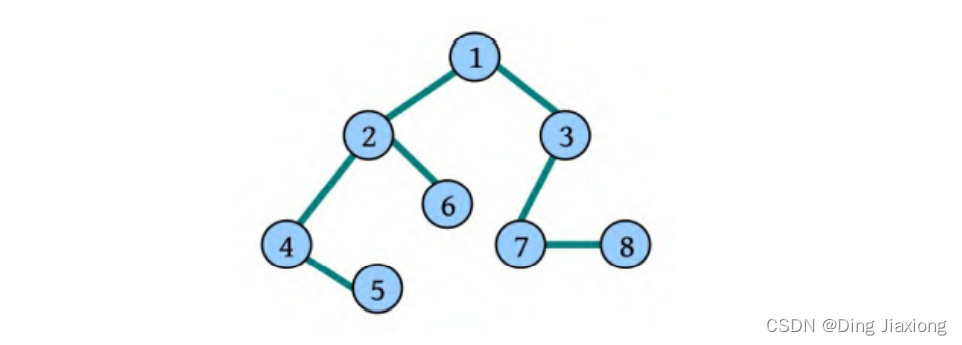
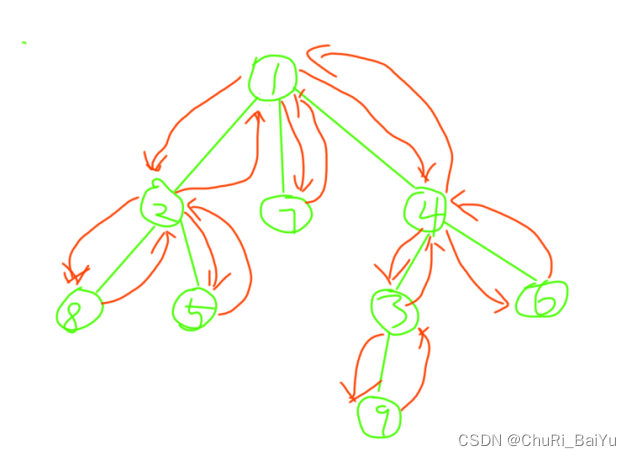
以图4为例,删除节点4。以节点4为根的子树其大小为4,删去节点4后可产生三个子树,其中以节点4为根的子树中产生了两个子树3,6,其大小为2,1。第三个子树不由以4为根的子树部分组成,而是由除以4为根的子树外的其他部分组成,其大小为整棵树大小减去以4为根的子树的大小。
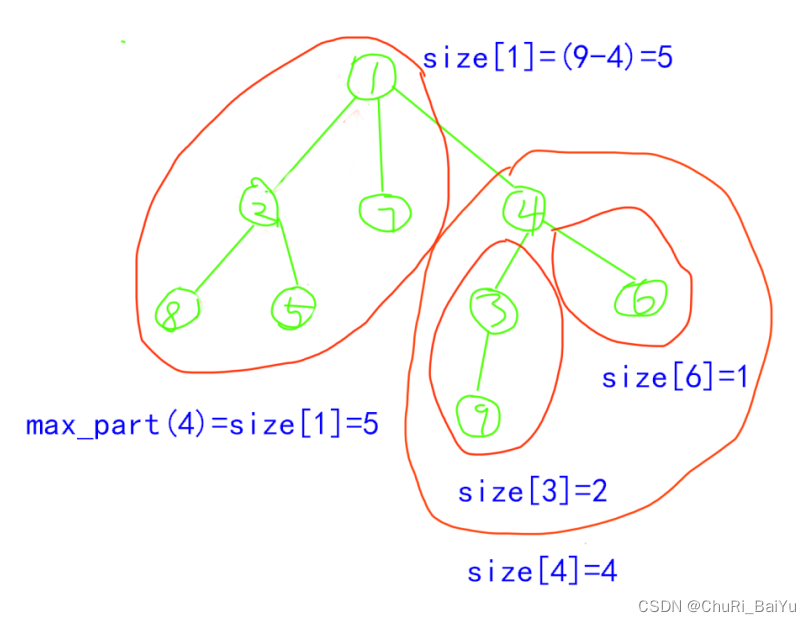
void dfs(int u){st[u]=true;size[u]=1; ///以u为根的子树初始时含有子树的根节点,其大小为1int max_part=0; ///存储在去除节点u后,产生的子树的最大值for(int i=h[u];i!=-1;i=ne[i]){int j=e[i];if(!st[j]) {dfs(j);size[u]+=size[j]; ///将子树u的其余部分加入到子树中///记录去除节点u后产生的子树中的最大值(以u根节点的子树中的一部分形成的子树)max_part=max(max_part,size[j]); }}///非以u根节点的子树中的一部分形成的子树,也需要比较记录max_part=max(max_part,n-size[u]);
///判断删除当前节点产生的最大子树是否比已记录的删去节点后产生的子树最大值中的最小值更小if(max_part<ans){ ans=max_part; ///将记录的最小值改为删去当前节点产生的子树最大值pos=u; ///记录该结点}
}5.图的连通块划分
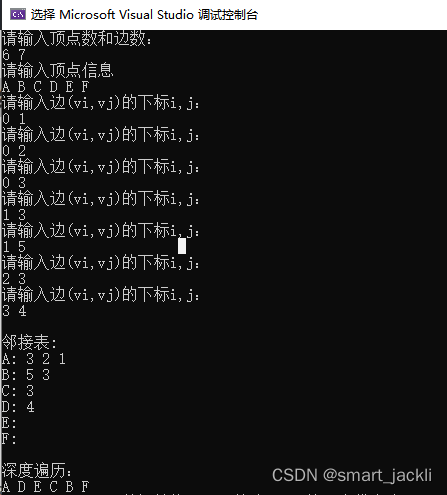
划分方法,将图的每一个没有被遍历过的点都遍历一次,将每一个遍历到的点所连通的点都记为同一个连通块。以图5为例。
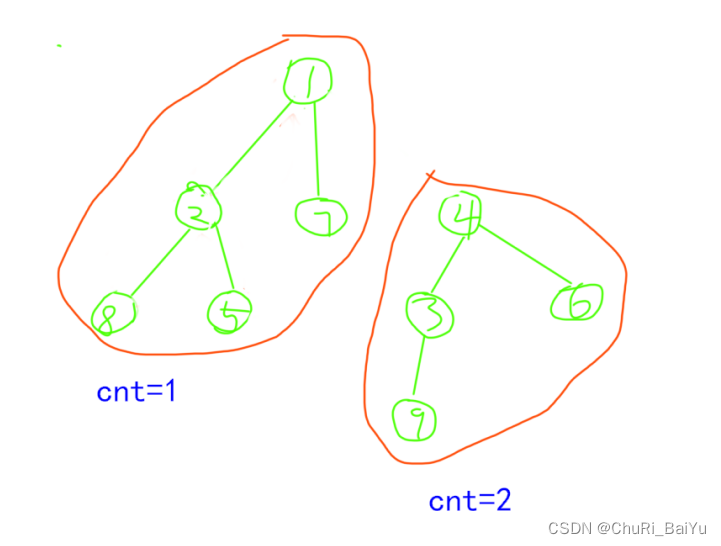
void dfs(int u){st[u]=true;v[u]=cnt; ///标记该点属于第cnt个连通块for(int i=h[u];i!=-1;i=ne[i]){int j=e[i];if(!st[j]) {dfs(j);}}
}
for(int i=1;i<=n;i++){if(!st[i]){cnt++; ///连通块个数dfs(i);}
}三、例题实践
1.树的重心例题实战
a.题目描述
给定一颗树,树中包含 n 个结点(编号 1∼n)和 n−1 条无向边。
请你找到树的重心,并输出将重心删除后,剩余各个连通块中点数的最大值。
重心定义:重心是指树中的一个结点,如果将这个点删除后,剩余各个连通块中点数的最大值最小,那么这个节点被称为树的重心。
输入格式
第一行包含整数 n,表示树的结点数。
接下来 n−1 行,每行包含两个整数 a 和 b,表示点 a 和点 b 之间存在一条边。
输出格式
输出一个整数 m,表示将重心删除后,剩余各个连通块中点数的最大值。
数据范围
1≤n≤1e5
输入样例
9
1 2
1 7
1 4
2 8
2 5
4 3
3 9
4 6
输出样例:
4
b.解题思路
思路:按题目要求操作
c.代码实现
#include<iostream>
#include<cstring>using namespace std;const int N=1e5+10,M=2*N;int ans=N;
int h[N],e[M],ne[M],idx;
bool st[N];
int n;void add(int a,int b){e[idx]=b;ne[idx]=h[a];h[a]=idx++;
}int dfs(int u){st[u]=true; ///标记已遍历过的点int size_u=1;///以u为根的子树初始时含有子树的根节点,其大小为1int max_part=0; ///存储在去除节点u后,产生的子树的最大值for(int i=h[u];i!=-1;i=ne[i]){///遍历与点u相连的点int j=e[i]; ///将与点u相连的点存入jif(!st[j]) {///若点j未被遍历过,则对与点j相连的点进行搜索int size_j=dfs(j);///记录去除节点u后产生的子树中的最大值(以u根节点的子树中的一部分形成的子树)max_part=max(max_part,size_j);size_u+=size_j;///将子树u的其余部分加入到子树中}}///非以u根节点的子树中的一部分形成的子树,也需要比较记录max_part=max(max_part,n-size_u);///与已记录的删去节点后产生的子树最大值中的最小值比较,取最小值ans=min(ans,max_part);return size_u;
}int main(){memset(h,-1,sizeof h); ///初始表头scanf("%d",&n);for(int i=0;i<n-1;i++) {int a,b;scanf("%d%d",&a,&b);add(a,b),add(b,a); ///添加双向边到图中}dfs(1);cout <<ans <<endl;return 0;
}