算法总结-深度优先遍历和广度优先遍历

article/2025/9/20 7:00:04

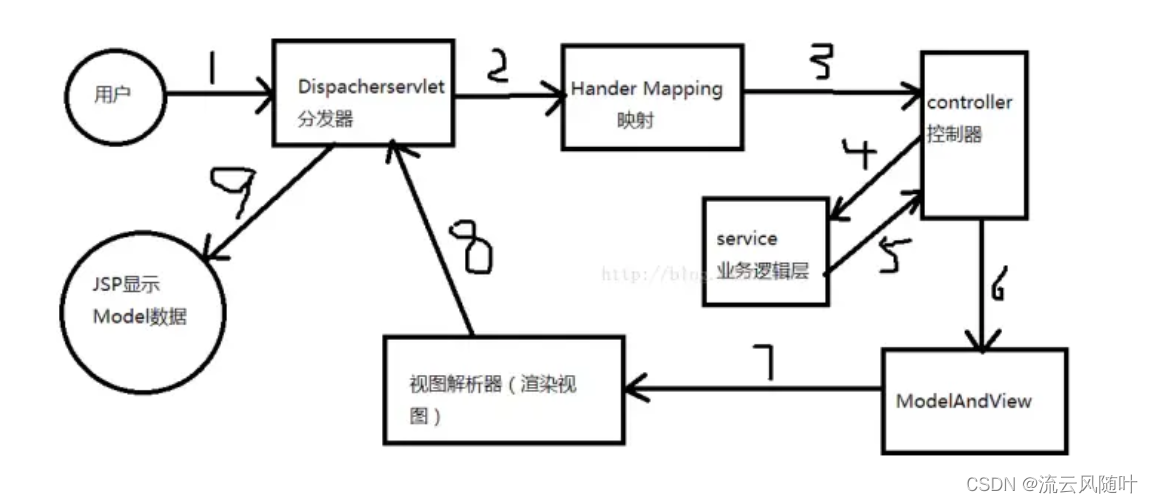
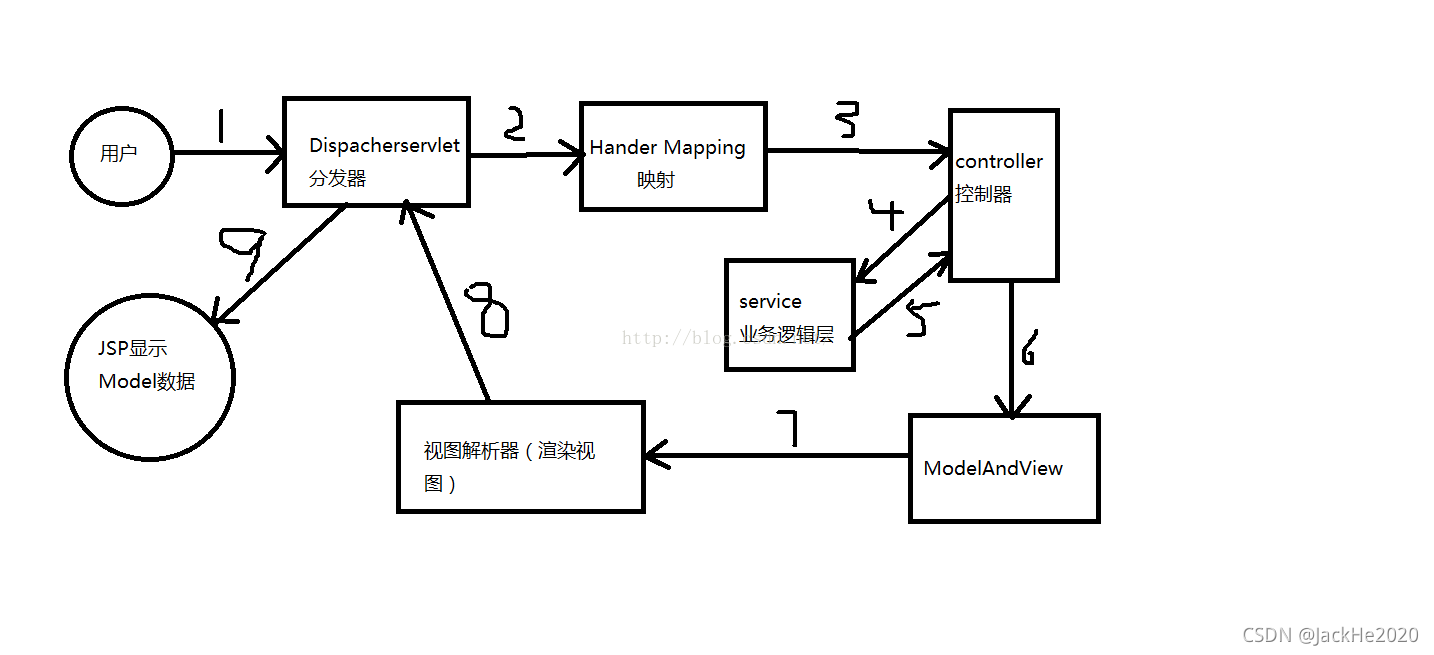
深度优先遍历(Depth First Search，简称DFS) 与广度优先遍历(Breath First Search，简称BFS)是图论中两种非常重要的算法，生产上广泛用于拓扑排序，寻路(走迷宫)，搜索引擎，爬虫等。

一、深度优先遍历
深度优先遍历的思路是从图的一个未访问的顶点V开始，沿着一条路一直走到底，然后从这条路尽头的节点回退到上一个节点，再从另一条路开始走到底，不断递归重复此过程…直到所有的顶点都遍历完成。它的特点说通俗了就是不撞南墙不回头，走完了一条路，再换一条路继续走。
树是图的一种特例（联通无环的图就是树），接下来我们来看树用深度优先遍历该怎么遍历。
1、深度优先遍历过程
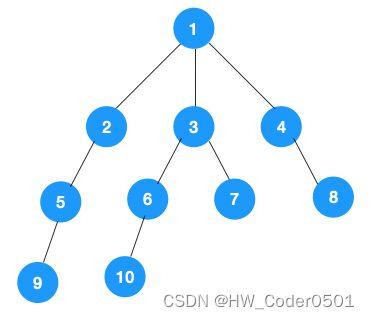
在这里插入图片描述
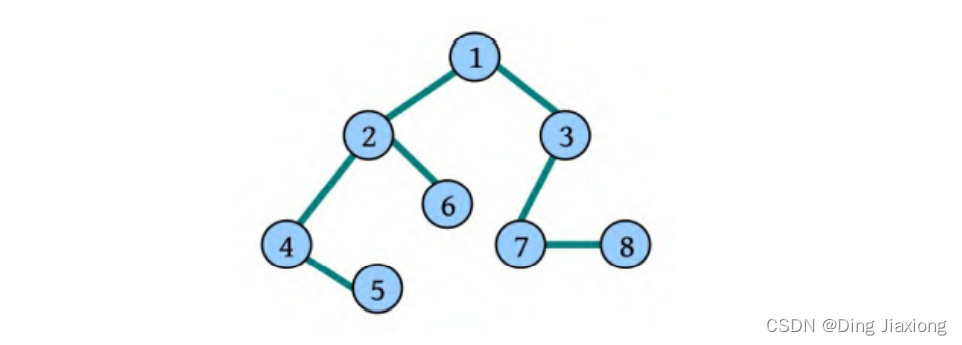
（1）、我们从根节点1开始深度优先遍历，它相邻的节点有2、3、4，依先遍历节点2，再遍历2的右边节点5，再遍历9，至此便无可遍历的节点。

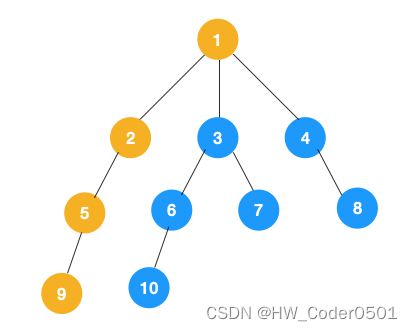
（2）、上图中一条路径已经遍历到底，此时从叶子节点9回退到上一节点5，，看下节点 5 是否还有除 9 以外的节点，没有继续回退到 2，2 也没有除 5 以外的节点，回退到 1，1 有除 2 以外的节点 3，所以从节点 3 开始进行深度优先遍历，如下：
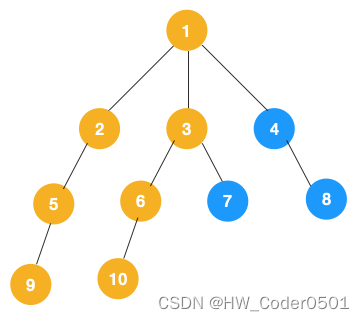
在这里插入图片描述
（3）、同理从 10 开始往上回溯到 6, 6 没有除 10 以外的子节点，再往上回溯，发现3有除 6 以外的子节点 7，所以此时会遍历 7。

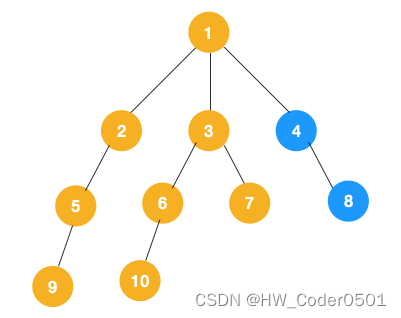
（4）、从 7 往上回溯到 3， 1，发现 1 还有节点 4 未遍历，所以此时沿着 4， 8 进行遍历，这样就完成了整个遍历过程。
完整的节点的遍历顺序如下(节点上的的蓝色数字代表)：
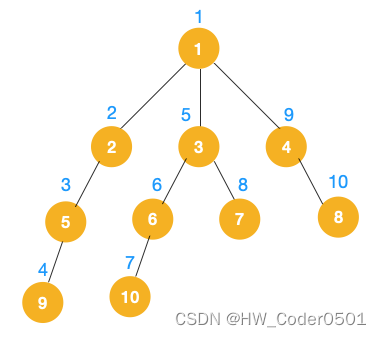
在这里插入图片描述
相信大家看到以上的遍历不难发现这就是树的前序遍历，实际上不管是前序遍历，还是中序遍历，亦或是后序遍历，都属于深度优先遍历。

那么深度优先遍历该怎么实现呢，有递归和非递归两种表现形式，接下来我们以二叉树为例来看下如何分别用递归和非递归来实现深度优先遍历。
2、深度优先遍历实现
（1）、递归
递归实现比较简单，由于是前序遍历，所以我们依次遍历当前节点，左节点，右节点即可，对于左右节点来说，依次遍历它们的左右节点即可，依此不断递归下去，直到叶节点(递归终止条件)，代码如下：

public class Solution { private static class Node { public int value;  // 节点值public Node left;  // 左节点  public Node right;  // 右节点public Node(int value, Node left, Node right) { this.value = value; this.left = left; this.right = right; } } public static void dfs(Node treeNode) { if (treeNode == null) { return; } process(treeNode);  // 遍历节点dfs(treeNode.left);  // 遍历左节点dfs(treeNode.right);  // 遍历右节点} 
}

递归的表达性很好，也很容易理解，不过如果层级过深，很容易导致栈溢出。所以我们重点看下非递归实现。
（2）、非递归
仔细观察深度优先遍历的特点，对二叉树来说，由于是先序遍历(先遍历当前节点，再遍历左节点，再遍历右节点)，所以我们有如下思路：

对于每个节点来说，先遍历当前节点，然后把右节点压栈，再压左节点(这样弹栈的时候会先拿到左节点遍历，符合深度优先遍历要求)。
弹栈，拿到栈顶的节点，如果节点不为空，重复步骤 1，如果为空，结束遍历。
我们以以下二叉树为例来看下如何用栈来实现 DFS。
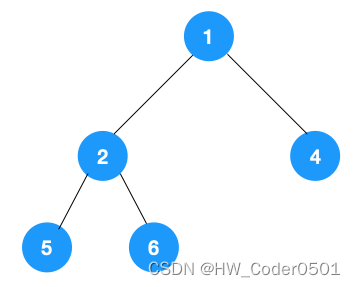
在这里插入图片描述

（a）先将根节点1压入栈中
在这里插入图片描述

（b）根节点弹出栈，把右节点和左节点依次压入栈中
在这里插入图片描述

（c）将节点2的右节点和左节点依次依次压入栈中
在这里插入图片描述

（d）按照5、6、4的顺序将节点弹出栈
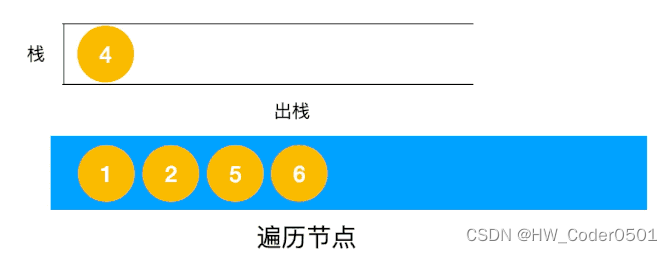
在这里插入图片描述

使用栈来将要遍历的节点压栈，然后出栈后检查此节点是否还有未遍历的节点，有的话压栈，没有的话不断回溯(出栈)，有了思路，不难写出如下用栈实现的二叉树的深度优先遍历代码：

/** * 使用栈来实现 dfs * @param root */ 
public static void dfsWithStack(Node root) { if (root == null) { return; } Stack<Node> stack = new Stack<>(); // 先把根节点压栈 stack.push(root); while (!stack.isEmpty()) { Node treeNode = stack.pop(); // 遍历节点 process(treeNode) // 先压右节点 if (treeNode.right != null) { stack.push(treeNode.right); } // 再压左节点 if (treeNode.left != null) { stack.push(treeNode.left); } } 
}

二、深度优先遍历
广度优先遍历，指的是从图的一个未遍历的节点出发，先遍历这个节点的相邻节点，再依次遍历每个相邻节点的相邻节点。

上面所述树的广度优先遍历动图如下，每个节点的值即为它们的遍历顺序。所以广度优先遍历也叫层序遍历，先遍历第一层(节点 1)，再遍历第二层(节点 2，3，4)，第三层(5，6，7，8)，第四层(9，10)。
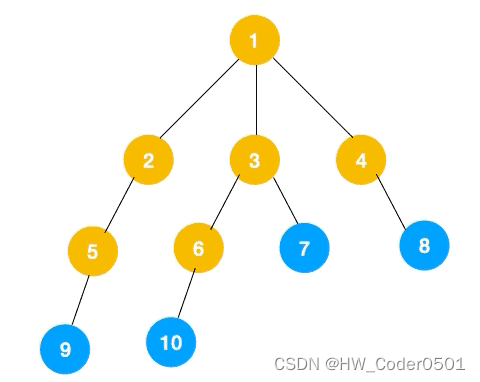
在这里插入图片描述

深度优先遍历用的是栈，而广度优先遍历要用队列来实现，我们以下图二叉树为例来看看如何用队列来实现广度优先遍历。
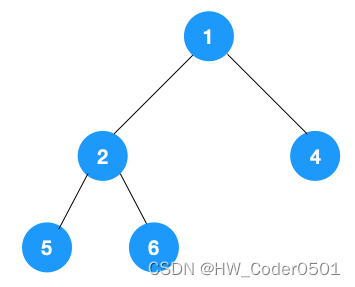
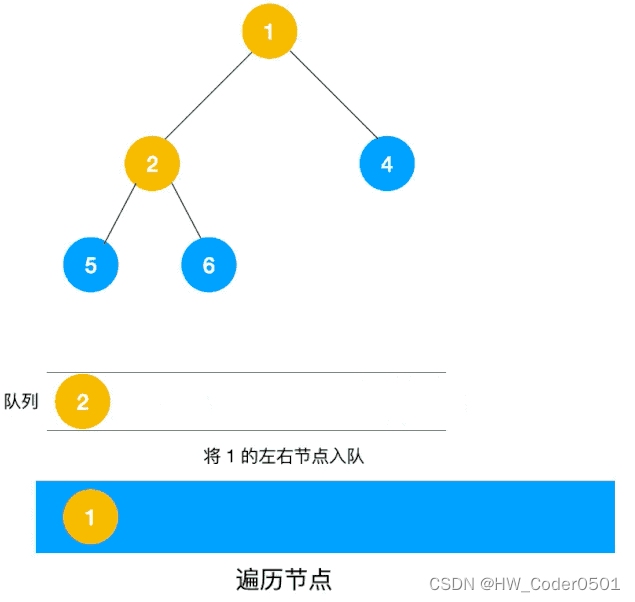
在这里插入图片描述

代码实现如下：

/** * 使用队列实现 bfs * @param root */ 
private static void bfs(Node root) { if (root == null) { return; } Queue<Node> stack = new LinkedList<>(); stack.add(root); while (!stack.isEmpty()) { Node node = stack.poll(); System.out.println("value = " + node.value); Node left = node.left; if (left != null) { stack.add(left); } Node right = node.right; if (right != null) { stack.add(right); } } 
}