图的深度优先遍历和广度优先遍历

本文参考自《大话数据结构》

文章目录

- 定义
- 图的存储结构
- - 邻接矩阵
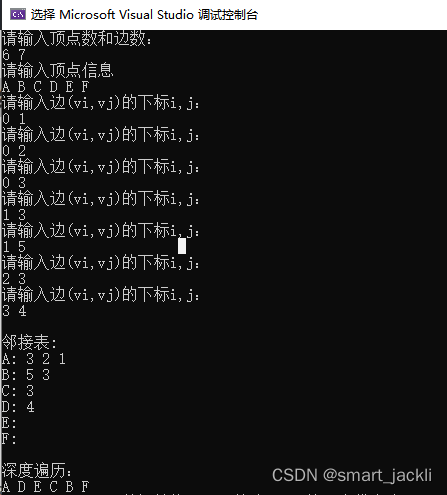
  - 邻接表
- 图的遍历
- - 深度优先遍历
  - - 邻接矩阵代码
    - 邻接表代码
  - 广度优先遍历
  - - 邻接矩阵
    - 邻接表
- 最小生成树
- 最短路径算法

定义

图(Graph) 是由顶点的有穷非空集合和顶点之间边的集合组成，通常表示为G(V，E)，其中，G表示一个图，V是图G中顶点的集合，E是图G中边的集合 。

图按照有无方向分为无向图 和有向图 。无向图由顶点和边构成，有向图由顶点和弧构成。弧有弧尾和弧头之分。
图按照边或弧的多少分稀疏图 和稠密图 。如果任意两个顶点之间都存在边叫完全图，有向的叫有向完全图。若无重复的边或顶点到自身的边则叫简单图。
图中顶点之间有邻接点、依附的概念。无向图顶点的边数叫做度，有向图顶点分为入度和出度。图上的边或弧上带权则称为网。
图中顶点间存在路径，两顶点存在路径则说明是连通的，如果路径最终回到起始点则称为环，当中不重复叫简单路径。若任意两顶点都是连通的，则图就是连通图 ，有向则称强连通图。图中有子图，若子图极大连通则就是连通分量，有向的则称强连通分量。
无向图中连通且n个顶点n-1条边叫生成树 。有向图中一顶点入度为 0其余顶点入度为1的叫有向树。一个有向图由若干棵有向树构成生成森林。

图的存储结构

邻接矩阵

图的邻接矩阵(Adjacency Matrix) 存储方式是用两个数组来表示图。一个一维数组存储图中顶点信息，一个二维数组(称为邻接矩阵)存储图中的边或弧的信息。

typedef char VertexType;//顶点类型
typedef int EdgeType;//边的权值类型
#define MAXVEX 100//最大顶点数
#define INFINITY 65535//用65535表示∞
typedef struct {VertexType vexs[MAXVEX];//顶点表EdgeType arc[MAXVEX][MAXVEX];//邻接矩阵int numVertexes, numEdges;//图中当前的顶点数和边数
}MGraph;

邻接表

邻接矩阵是不错的一种图存储结构，但是我们也发现，对于边数相对顶点较少的图，这种结构是存在对存储空间的极大浪费的。

因此我们考虑另外-种存储结构方式。回忆我们在线性表时谈到，顺序存储结构就存在预先分配内存可能造成存储空间浪费的问题，于是引出了链式存储的结构。同样的，我们也可以考虑对边或弧使用链式存储的方式来避免空间浪费的问题。

再回忆我们在树中谈存储结构时，讲到了一种孩子表示法，将结点存入数组，并对结点的孩子进行链式存储，不管有多少孩子，也不会存在空间浪费问题。这个思路同样适用于图的存储。我们把这种数组与链表相结合的存储方法称为邻接表(Adjacency List)。

邻接表的处理办法是这样的：

图中顶点用一个一维数组存储，当然，顶点也可以用单链表来存储，不过数组可以较容易地读取顶点信息，更加方便。另外，对于顶点数组中，每个数据元素还需要存储指向第一一个邻接点的指针，以便于查找该顶点的边信息。
图中每个顶点Vi的所有邻接点构成一个线性表，由于邻接点的个数不定，所以用单链表存储，无向图称为顶点v1的边表，有向图则称为顶点VI作为弧尾的出边表。

图片来源：《大话数据结构》
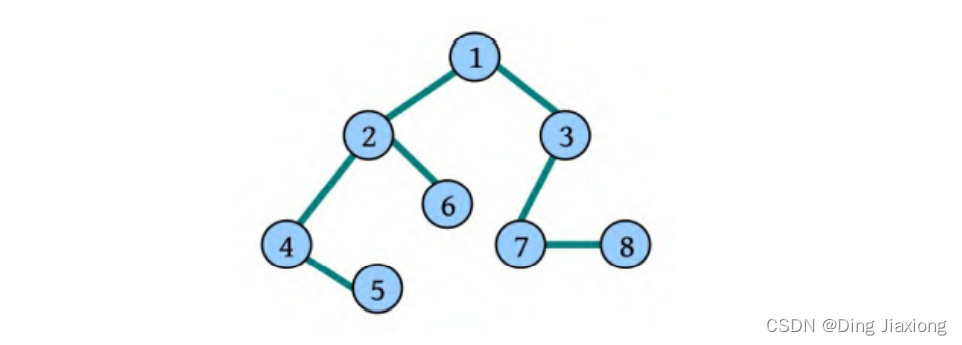
若是有向图，邻接表结构是类似的，比如图7-4-7 中第一幅图的邻接表就是第二幅图。但要注意的是有向图由于有方向，我们是以顶点为弧尾来存储边表的，这样很容易就可以得到每个顶点的出度。但也有时为了便于确定顶点的入度或以顶点为弧头的弧，我们可以建立一个有向图的逆邻接表，即对每个顶点Vi都建立一个链接为v为弧头的表。
图片来源：《大话数据结构》
对于带权值的网图，可以在边表结点定义中再增加一一个 weight的数据域，存储权对于带权值的网图，可以在边表结点定义中再增加一一个 weight的数据域，存储权值信息即可，如图7-4-8所示。
在这里插入图片描述

typedef struct EdgeNode {//边表节点int adjvex;//邻接点域，存储该顶点对应的下标EdgeType weight;//用于存储权值，对于非网图可以不需要struct EdgeNode* next;//指向下一个邻接点
}EdgeNode;typedef struct VertexNode {//顶点表节点VertexType data;//顶点域，存储顶点信息EdgeNode* firstedge;//边表头指针
}VertexNode, AdjList[MAXVEX];typedef struct {AdjList adjList;int numVertexes, numEdges;//图中当前的顶点数和边数
}GraphAdjList;

图的遍历

从图中某一顶点出发访遍图中其余顶点，且使每一个顶点仅被访问一次，这一过程就叫做图的遍历(Traversing Graph)。

深度优先遍历

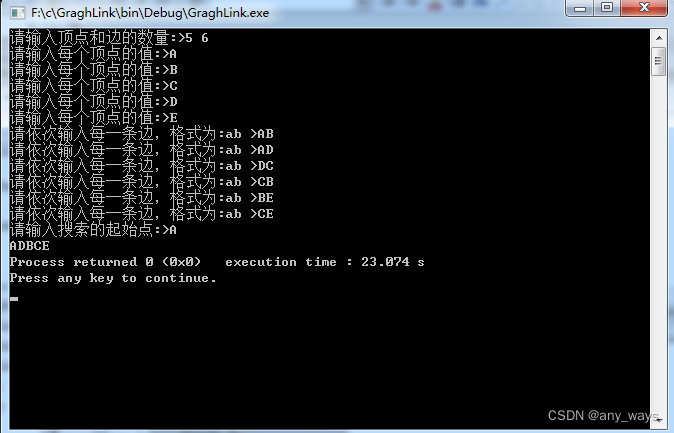
深度优先遍历(Depth, First Search),也有称为深度优先搜索，简称为DFS。

它就是。它从图中某个顶点v出发，访问此顶点，然后从v的未被访问的邻接点出发深度优先遍历图，直至图中所有和v有路径相通的顶点都被访问到。事实上，我们这里讲到的是连通图，对于非连通图，只需要对它的连通分量分别进行深度优先遍历，即在先前一个顶点进行一次深度优先遍历后，若图中尚有顶点未被访问，则另选图中一个未曾被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

邻接矩阵代码

#define TRUE 1
#define FALSE 0
#define MAXVEX 100//最大顶点数typedef int Boolean;
typedef char VertexType;//顶点类型
typedef int EdgeType;//边的权值类型typedef struct {VertexType vexs[MAXVEX];//顶点表EdgeType arc[MAXVEX][MAXVEX];//邻接矩阵int numVertexes, numEdges;//图中当前的顶点数和边数
}MGraph;Boolean visited[MAXVEX];
//邻接矩阵的深度优先递归算法
void DFS(MGraph G, int i) {int j;visited[i] = TRUE;cout << G.vexs[i] << " ";for (j = 0; j < G.numVertexes; j++) {//若两点连通且未被访问过if (G.arc[i][j] == 1 && !visited[j])DFS(G, j);}
}//邻接矩阵的深度遍历操作
void DFSTraverse(MGraph G) {int i;for (i = 0; i < G.numVertexes; i++)visited[i] = FALSE;//初始化顶点状态，所有顶点都是未访问过的状态for (i = 0; i < G.numVertexes; i++)if (!visited[i])//对未访问过的顶点调用DFS，若是连通图，只会执行一次DFS(G, i);
}

邻接表代码

typedef struct EdgeNode {//边表节点int adjvex;//邻接点域，存储该顶点对应的下标EdgeType weight;//用于存储权值，对于非网图可以不需要struct EdgeNode* next;//指向下一个邻接点
}EdgeNode;typedef struct VertexNode {//顶点表节点VertexType data;//顶点域，存储顶点信息EdgeNode* firstedge;//边表头指针
}VertexNode, AdjList[MAXVEX];typedef struct {AdjList adjList;int numVertexes, numEdges;//图中当前的顶点数和边数
}GraphAdjList;void DFS(GraphAdjList GL, int i) {EdgeNode* p;visited[i] = TRUE;cout << GL.adjList[i].data << ' ';p = GL.adjList[i].firstedge;while (p) {if (!visited[p->adjvex])DFS(GL, p->adjvex);//对未访问的邻接顶点递归调用p = p->next;}
}void DFSTraverse(GraphAdjList GL) {int i;for (i = 0; i < GL.numVertexes; i++)visited[i] = FALSE;//初始化所有未访问节点for (i = 0; i < GL.numVertexes; i++)if (!visited[i])//对所有未访问顶点调用DFS，若是连通图，则只会调用一次DFS(GL, i);
}

对比两个不同存储结构的深度优先遍历算法，对于n个顶点e条边的图来说，邻接矩阵由于是二维数组，要查找每个顶点的邻接点需要访问矩阵中的所有元素，因此都需要O（n²）的时间。而邻接表做存储结构时，找邻接点所需的时间取决于顶点和边的数量，所以是O（n+e）。显然对于点多边少的稀疏图来说，邻接表结构使得算法在时间效率上大大提高。

广度优先遍历

广度优先遍历(Breadth _First _Search)，又称为广度优先搜索，简称BFS。
如果说图的深度优先遍历类似树的前序遍历，那么图的广度优先遍历就类似于树的层序遍历。

邻接矩阵

//#define TRUE 1
//#define FALSE 0
//
//typedef int Boolean;
//typedef char VertexType;//顶点类型
//typedef int EdgeType;//边的权值类型
//#define MAXVEX 100//最大顶点数
//#define INFINITY 65535//用65535表示∞
//#define MAXSIZE 20
//#define OK 1
//#define ERROR 0
//
//typedef int QElemType;//数据类型
//typedef int Status;//函数类型
//
//typedef struct Queue {
//	QElemType data[MAXSIZE];
//	int front;//头指针
//	int rear;//尾指针，若队列不空，指向队列尾部元素的下一个位置
//}SqQueue;
//
初始化一个空队列Q
//Status InitQueue(SqQueue* Q) {
//	Q->front = 0;
//	Q->rear = 0;
//	return OK;
//}
//
循环队列的入队操作
若队列未满，则插入元素e为Q新的队尾元素
//Status EnQueue(SqQueue* Q, QElemType e) {
//	if ((Q->rear + 1) % MAXSIZE == Q->front)return ERROR;//队列满了，新元素爬开
//	Q->data[Q->rear] = e;//将元素e赋值给队尾
//	Q->rear = (Q->rear + 1) % MAXSIZE;//rear指针向后移动一位，若到最后则转到数组头部
//	return OK;
//}
//
//Status QueueEmpty(SqQueue Q) {
//	if (Q.rear == Q.front)return TRUE;
//	else return FALSE;
//}
//
循环队列的出队操作
若队列不空，则删除Q中队头元素，用e返回其值
//Status DeQueue(SqQueue* Q, QElemType* e) {
//	if (Q->front == Q->rear)return ERROR;//队伍是空的，憨批
//	*e = Q->data[Q->front];//将队头元素赋值给e
//	Q->front = (Q->front + 1) % MAXSIZE;//front指针向后移动一位，若到最后则转到数组头部
//	return OK;
//}
//
//typedef struct {
//	VertexType vexs[MAXVEX];//顶点表
//	EdgeType arc[MAXVEX][MAXVEX];//邻接矩阵
//	int numVertexes, numEdges;//图中当前的顶点数和边数
//}MGraph;
//
//Boolean visited[MAXVEX];
void BFSTraverse(MGraph G) {int i, j;Queue Q;for (i = 0; i < G.numVertexes; i++)visited[i] = FALSE;InitQueue(&Q);//初始化一个辅助用的队列for (i = 0; i < G.numVertexes; i++) {//对每一个顶点做循环if (!visited[i]) {//若是当前顶点未访问过visited[i] = TRUE;//设置为访问过cout << G.vexs[i] << ' ';EnQueue(&Q, i);//将此顶点入队while (!QueueEmpty(Q)) {//若当前队列不空DeQueue(&Q, &i);//将队中元素出列，赋值给ifor (j = 0; j < G.numVertexes; j++){//判断其他顶点与当前顶点存在边且未访问过if (G.arc[i][j] == 1 && !visited[j]) {//将找到的此顶点标记为已访问visited[j] = TRUE;cout << G.vexs[j] << ' ';EnQueue(&Q, j);//将找到的此顶点入队}}}}}
}

邻接表

懒得写了，先欠着
对比图的深度优先遍历与广度优先遍历算法，你会发现，它们在时间复杂度上是一样的，不同之处仅仅在于对顶点访问的顺序不同。可见两者在全图遍历上是没有优劣之分的，只是视不同的情况选择不同的算法。

最小生成树

最小生成树很简单，两种方法：

在图中依次拿出使得现有生成子图无环的权值最小的边即可
在图中依次去掉可以成环的权值最大的边即可

最短路径算法

dijkstra算法参考这里：https://blog.csdn.net/qq_35644234/article/details/60870719
Floyd算法参考这里：https://blog.csdn.net/ljhandlwt/article/details/52096932
https://blog.csdn.net/jeffleo/article/details/53349825