1.先序序列为a,b,c,d 的不同二叉树的个数是 （14） 。

• 13

• 14

• 15

• 16

• f（n）=c(n  2n)/n+1

2.在构建哈弗曼树时，要使树的带权路径长度最小，只需要遵循一个原则，那就是：权重越大的结点离树根越近。

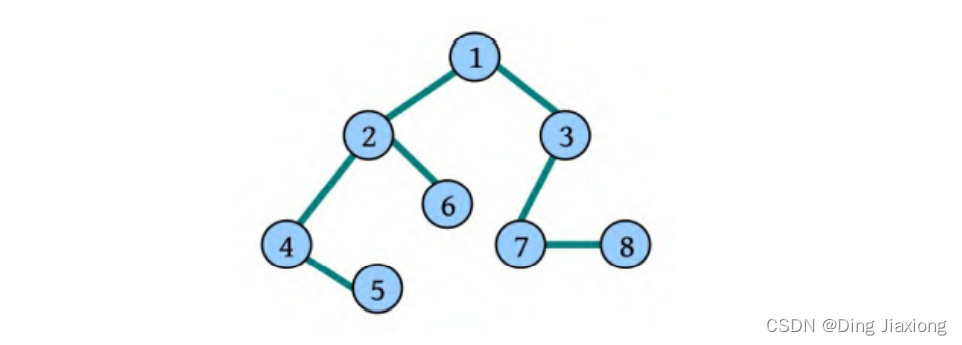
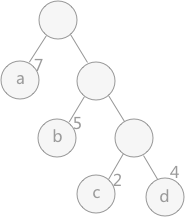
树的带权路径长度为树中所有叶子结点的带权路径长度之和。通常记作 “WPL” 。例如图 1 中所示的这颗树的带权路径长度为：

WPL = 7 * 1 + 5 * 2 + 2 * 3 + 4 * 3

 

 3.

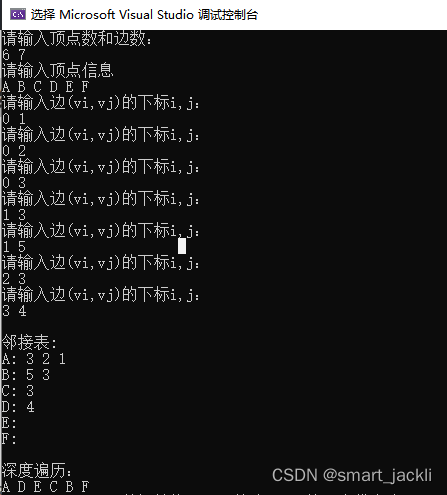
深度优先遍历序列为：2 1 5 6 3 4 7 8
若从3出发的深度优先遍历序列为：3 4 7 6 2 1 5 8
若从3出发的深度优先遍历序列为：1 2 6 3 4 7 8 5

 

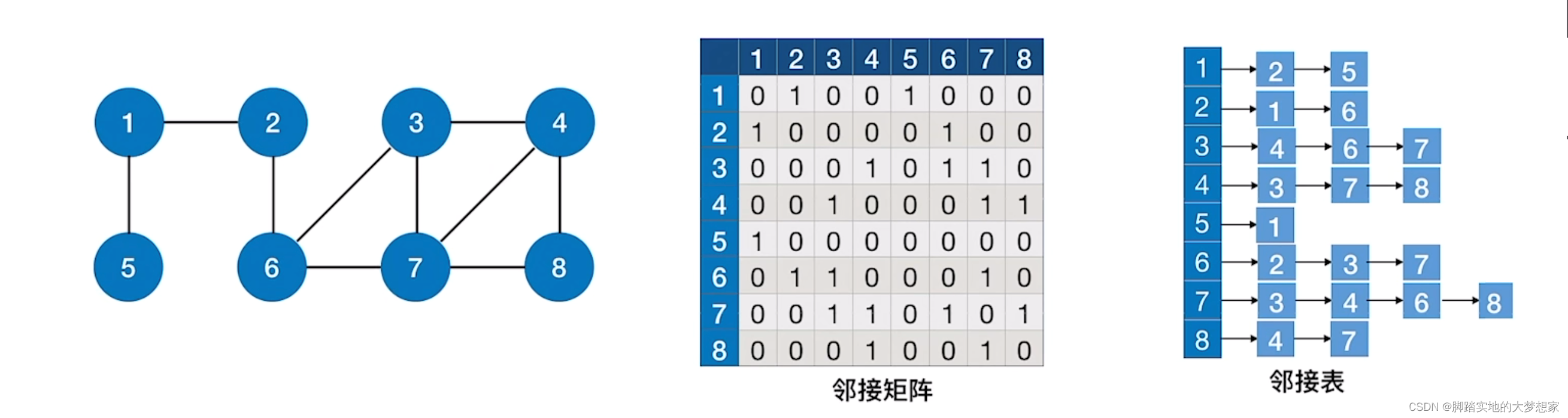
深度优先时间复杂度
深度优先的时间复杂度主要也是消耗在了对顶点的访问以及探索顶点有多少条边。

邻接矩阵
如果采用临界矩阵的存储方法，所消耗的时间复杂度为：
访问V个顶点需要O(V)的时间；
查找每个顶点的邻接点都需要O(V)的时间，总共需要O(V2)的时间；
所以时间复杂度为：O(V)+O(V2)
根据大O表示法，最终的时间复杂度为 O(V2)

邻接表
如果采用邻接表的存储方法，所消耗的时间复杂度为：
访问V个顶点需要O(V)的时间；
查找每个顶点的邻接点共需要两倍的边的总数的时间，即O(2E)的时间；
所以时间复杂度为：O(V)+O(2E)
根据大O表示法，最终的时间复杂度为 O(V)+O(E)

 4.

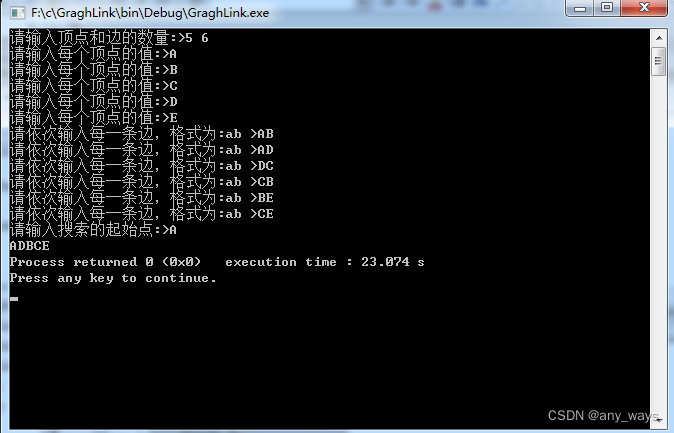
克鲁斯卡尔算法介绍. 克鲁斯卡尔 (Kruskal)算法，是用来求加权连通图的最小生成树的算法。. 基本思想：按照权值从小到大的顺序选择n-1条边，并保证这n-1条边不构成回路。. 具体做法：首先构造一个只含n个顶点的森林，然后依权值从小到大从连通网中选择边加入到森林中，并使森林中不产生回路，直至森林变成一棵树为止。.

 5.

Kruskal算法是一种贪心算法，我们将图中的每个edge按照权重大小进行排序，每次从边集中取出权重最小且两个顶点都不在同一个集合的边加入生成树中！注意：如果这两个顶点都在同一集合内，说明已经通过其他边相连，因此如果将这个边添加到生成树中，那么就会形成环！这样反复做，直到所有的节点都连接成功！

 

 6.

Prim算法（普里姆算法）

Prim算法是另一种贪心算法，和Kuskral算法的贪心策略不同，Kuskral算法主要对边进行操作，而Prim算法则是对节点进行操作，每次遍历添加一个点，这时候我们就不需要使用并查集了。具体步骤为：

 

 7.

KMP 算法（Knuth-Morris-Pratt 算法）是一个著名的字符串匹配算法，效率很高，但是确实有点复杂。

 

暴力的字符串匹配算法很容易写，看一下它的运行逻辑：

// 暴力匹配（伪码）
int search(String pat, String txt) {int M = pat.length;int N = txt.length;for (int i = 0; i <= N - M; i++) {int j;for (j = 0; j < M; j++) {if (pat[j] != txt[i+j])break;}// pat 全都匹配了if (j == M) return i;}// txt 中不存在 pat 子串return -1;
}

 8.折半查找

折半查找算法

对静态查找表{5,13,19,21,37,56,64,75,80,88,92}采用折半查找算法查找关键字为 21 的过程为：
 

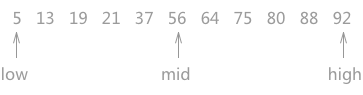
图 1 折半查找的过程（a）

如上图 1 所示，指针 low 和 high 分别指向查找表的第一个关键字和最后一个关键字，指针 mid 指向处于 low 和 high 指针中间位置的关键字。在查找的过程中每次都同 mid 指向的关键字进行比较，由于整个表中的数据是有序的，因此在比较之后就可以知道要查找的关键字的大致位置。

例如在查找关键字 21 时，首先同 56 作比较，由于21 < 56，而且这个查找表是按照升序进行排序的，所以可以判定如果静态查找表中有 21 这个关键字，就一定存在于 low 和 mid 指向的区域中间。

因此，再次遍历时需要更新 high 指针和 mid 指针的位置，令 high 指针移动到 mid 指针的左侧一个位置上，同时令 mid 重新指向 low 指针和 high 指针的中间位置。如图 2 所示：
 

图 2 折半查找的过程（b）
 

同样，用 21 同 mid 指针指向的 19 作比较，19 < 21，所以可以判定 21 如果存在，肯定处于 mid 和 high 指向的区域中。所以令 low 指向 mid 右侧一个位置上，同时更新 mid 的位置。
 

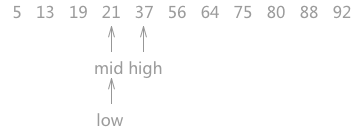
图 3 折半查找的过程（3）

当第三次做判断时，发现 mid 就是关键字 21 ，查找结束。

1. //折半查找算法
2. int Search_Bin(SSTable *ST,keyType key){
3. int low=1;//初始状态 low 指针指向第一个关键字
4. int high=ST->length;//high 指向最后一个关键字
5. int mid;
6. while (low<=high) {
7. mid=(low+high)/2;//int 本身为整形，所以，mid 每次为取整的整数
8. if (ST->elem[mid].key==key)//如果 mid 指向的同要查找的相等，返回 mid 所指向的位置
9. {
10. return mid;
11. }else if(ST->elem[mid].key>key)//如果mid指向的关键字较大，则更新 high 指针的位置
12. {
13. high=mid-1;
14. }
15. //反之，则更新 low 指针的位置
16. else{
17. low=mid+1;
18. }
19. }
20. return 0;
21. }