图的遍历（深度优先搜索）

1、深度优先搜索遍历过程

图的深度优先搜索(Depth First Search)，和树的先序遍历比较类似。

它的思想：假设初始状态是图中所有顶点均未被访问，则从某个顶点v出发，首先访问该顶点，然后依次从它的各个未被访问的邻接点出发深度优先搜索遍历图，直至图中所有和v有路径相通的顶点都被访问到。若此时尚有其他顶点未被访问到，则另选一个未被访问的顶点作起始点，重复上述过程，直至图中所有顶点都被访问到为止。

显然，深度优先搜索是一个递归的过程

深度优先遍历特点是，选定一个出发点后进行遍历，能前进则前进，若不能前进，回退一步再前进，或再回退一步后继续前进。依此重复，直到所有与选定点相通的所有顶点都被遍历。

2、示例

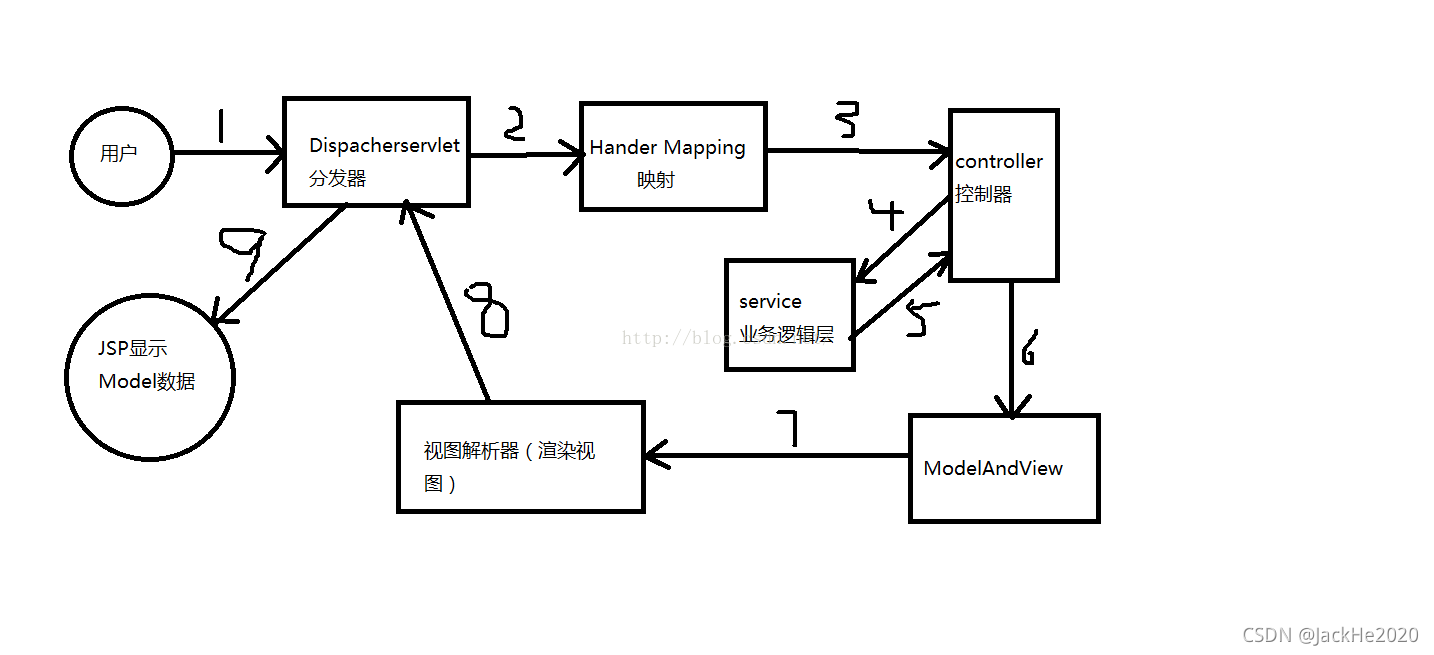
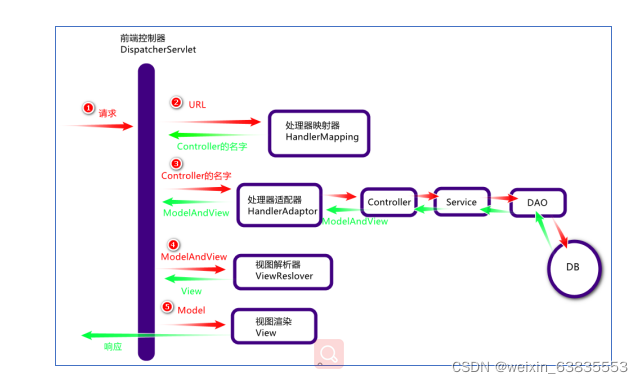
对图7-25连通无向图采用深度优先搜索遍历可得到顶点访问序列：v0,v1,v3,v7,v4,v8,v2,v5,v6

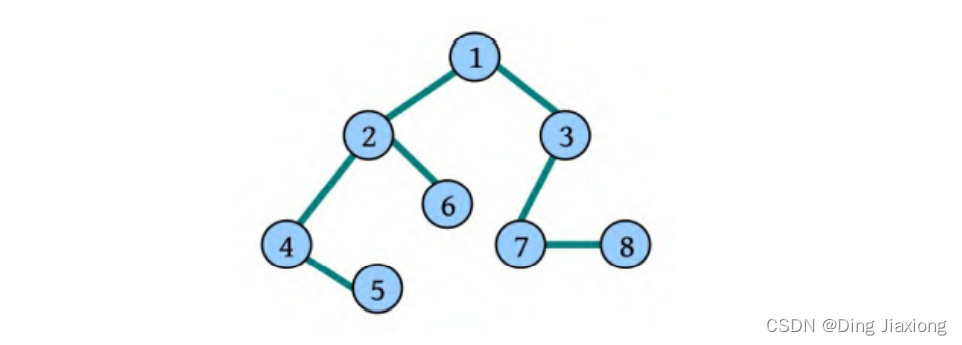
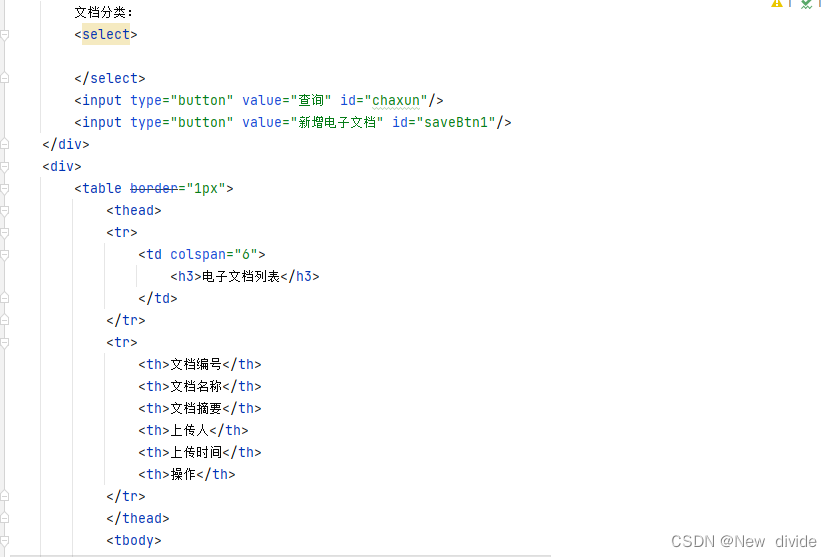
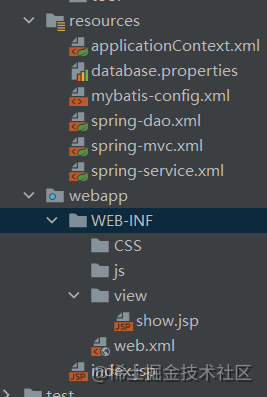
对图7-26连通无向图采用深度优先搜索遍历可得到顶点访问序列：v0,v1,v3,v2,v4,v5,v6,v7

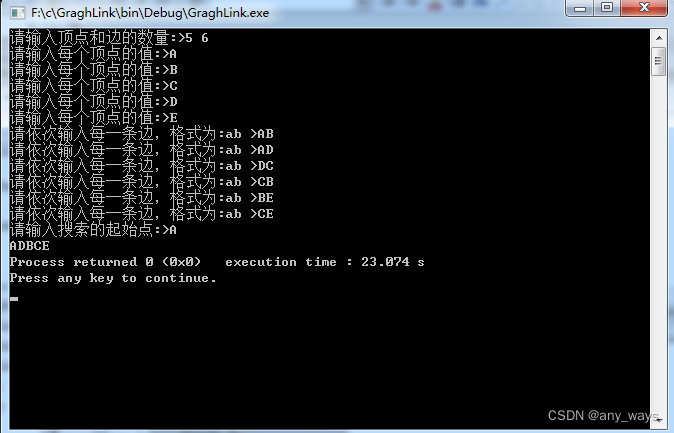
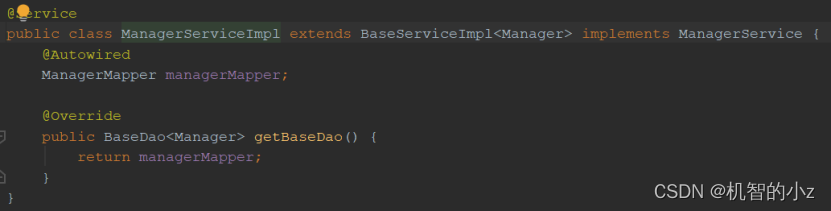
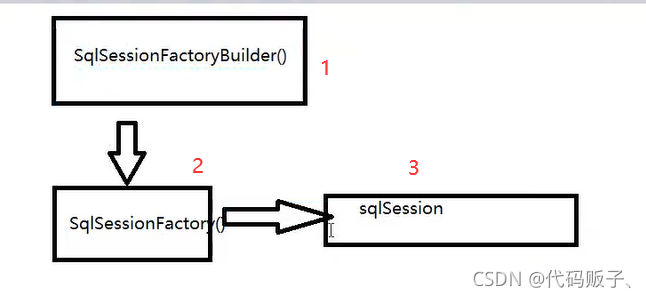
对图7-27连通无向图采用深度优先搜索遍历可得到顶点访问序列:v0,v1,v4,v3,v2或v2,v3,v0,v1,v4或v2,v1,v0,v4,v3

3、连通图的深度优先遍历

给定一图G=<V,E>，用visited[i]表示顶点i的访问情况，初值设为0，表示所有顶点未被访问过，当顶点被访问过时置1。则初始情况下所有的visited[i]都为0。假设从顶点V0开始遍历，则下一个遍历的顶点是V0的第一个邻接点Vi，接着遍历Vi的第一个邻接点Vj，……直到所有的顶点都被访过。

4、代码

无向图，邻接矩阵存储：

对图7-25深度优先遍历：

#include <iostream>
using namespace std;
#define INFINITY  65535 /* 表示权值的无穷*/
typedef int EdgeType;//边上的权值类型
typedef int VertexType;//顶点类型
const int MaxSize=100;
int visited[MaxSize];//全局标识数组class MGraph//邻接矩阵类
{public:MGraph(){vertexNum=0;edgeNum=0;}MGraph(VertexType a[],int n);//构造函数，初始化具有n个顶点的零图void CreateMGraph1(MGraph *Gp);//建立无向图的邻接矩阵void DFS(int v);//从v出发深度优先遍历的递归函数void DFS1(int v);//从v出发深度优先遍历的非递归函数public:int vertexNum,edgeNum;//顶点数和边数EdgeType adj[MaxSize][MaxSize];//邻接矩阵VertexType vertex[MaxSize];//顶点表
};
//构造函数，初始化具有n个顶点的零图
MGraph::MGraph(VertexType a[],int n)
{vertexNum=n;edgeNum=0;for(int i=0;i<n;i++) vertex[i]=a[i];for(int i=0;i<n;i++)for(int j=0;j<n;j++)adj[i][j]=0;
}//建立无向图的邻接矩阵表示
void MGraph::CreateMGraph1(MGraph *Gp)
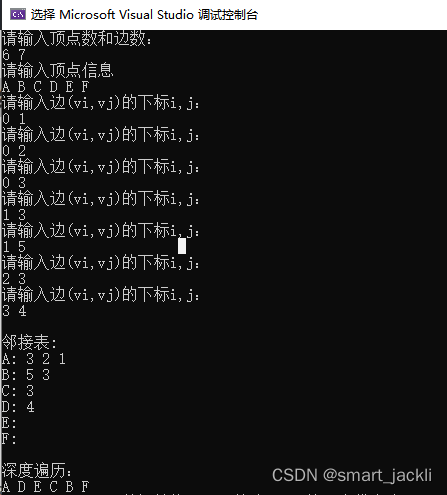
{int i, j, k;cout << "请输入顶点数和边数（空格分隔）：" << endl;cin >> Gp->vertexNum >> Gp->edgeNum;cout << "请输入顶点信息（空格分隔）：" << endl;for (i = 0; i < Gp->vertexNum; i++)cin >> Gp->vertex[i];for (i = 0; i < Gp->vertexNum; i++){for (j = 0; j < Gp->vertexNum; j++)Gp->adj[i][j] = 0;}for (k = 0; k < Gp->edgeNum; k++){cout << "请输入边（vi, vj)的上标i，下标j（空格分隔）:" << endl;cin >> i >> j;Gp->adj[i][j] = 1;Gp->adj[j][i] = 1;// 因为是无向图，矩阵对称}
}//从v出发深度优先遍历的递归函数
void MGraph::DFS(int v)
{int n=vertexNum;//顶点数目if(v<0||v>=n) throw "位置出错";cout<<vertex[v]<<" ";//输出顶点vvisited[v]=1;//被访问过for(int j=0;j<n;j++)if(visited[j]==0&&adj[v][j]==1)//没被访问过且存在边(v,j)DFS(j);
}
//从v出发深度优先遍历的非递归函数
void MGraph::DFS1(int v)
{int S[MaxSize],n=vertexNum,top=-1,j;if(v<0||v>=n) throw "位置出错";cout<<vertex[v]<<" ";//输出顶点vvisited[v]=1;//被访问过S[++top]=v;//顶点v进栈while(top!=-1){v=S[top];//栈顶元素出栈for(j=0;j<n;j++){if(visited[j]==0&&adj[v][j]==1)//没被访问过且存在边(v,j){cout<<vertex[j]<<" ";visited[j]=1;S[++top]=j;break;}}if(j==n) top--;}
}
int main()
{MGraph grph;grph.CreateMGraph1(&grph);for(int i=0;i<MaxSize;i++)visited[i]=0;for(int i=0;i<grph.vertexNum;i++){for(int j=0;j<grph.vertexNum;j++){cout<<grph.adj[i][j]<<" ";}cout<<endl;}cout<<"递归深度优先遍历结果："<<endl;grph.DFS(0);for(int i=0;i<MaxSize;i++)visited[i]=0;cout<<endl<<"非递归深度优先遍历结果："<<endl;grph.DFS1(0);return 0;
}

无向图，邻接表存储：

图7-25：

#include <iostream>
using namespace std;
#define INFINITY  65535 /* 表示权值的无穷*/
typedef int EdgeType;//边上的权值类型
typedef int VertexType;//顶点类型
const int MaxSize=100;
int visited[MaxSize];//全局标识数组
//无向图邻接表。边表结点结构
struct EdgeNode
{int adjvex;//邻接点域EdgeNode *next;//指向下一个边结点的指针
};
//无向图邻接表。表头结点结构
struct VexNode
{VertexType vertex;//顶点EdgeNode *firstedge;//边表的头指针
};
//邻接表类
class ALGraph
{public:ALGraph()//无参构造函数{vertexNum=0;edgeNum=0;for(int i=0;i<MaxSize;i++)adjlist[i].firstedge=NULL;}ALGraph(VertexType a[],int n);//有参构造函数void createGraph(int start, int end);//创建图,采取前插法void DFSL(int v);//从v出发深度优先遍历可达顶点递归函数void DFSL1(int v);//从v出发深度优先遍历可达顶点的非递归函数void displayGraph(int nodeNum);//打印void CountComp(ALGraph g);//求连通分量数，判断图的连通性private:VexNode adjlist[MaxSize];//存放顶点表的数组int vertexNum,edgeNum;//图的顶点数和边数
};
//有参构造函数。构造顶点表
ALGraph::ALGraph(VertexType a[],int n)
{vertexNum=n;edgeNum=0;for(int i=0;i<vertexNum;i++){adjlist[i].vertex=a[i];adjlist[i].firstedge=NULL;}
}
//创建图,采取前插法
void ALGraph::createGraph(int start, int end)
{//边(start,end)//adjlist[start].vertex=start;//表头结点中的顶点EdgeNode *p=new EdgeNode;//边结点p->adjvex=end;//邻接点//p->weight=weight;p->next=adjlist[start].firstedge;//前插法插入边结点padjlist[start].firstedge=p;
}
//打印存储的图
void ALGraph::displayGraph(int nodeNum)
{int i,j;EdgeNode *p;for(i=0;i<nodeNum;i++){p=adjlist[i].firstedge;while(p){cout<<'('<<adjlist[i].vertex<<','<<p->adjvex<<')'<<endl;p=p->next;}}
}
//从v出发深度优先遍历可达顶点递归函数
void ALGraph::DFSL(int v)
{int n=vertexNum;int j;EdgeNode *p;if(v>=n||v<0) throw "位置出错";cout<<adjlist[v].vertex<<" ";visited[v]=1;p=adjlist[v].firstedge;while(p){j=p->adjvex;//顶点if(visited[j]==0) DFSL(j);p=p->next;}
}
//从v出发深度优先遍历可达顶点的非递归函数
void ALGraph::DFSL1(int v)
{int S[MaxSize],top=-1,j,n=vertexNum;EdgeNode *p;if(v>=n||v<0) throw "位置出错";cout<<adjlist[v].vertex<<" ";visited[v]=1;S[++top]=v;//v进栈while(top!=-1){v=S[top];//栈顶元素出栈p=adjlist[v].firstedge;while(p){j=p->adjvex;//顶点if(visited[j]==1) p=p->next;else{cout<<adjlist[j].vertex<<" ";visited[j]=1;S[++top]=j;//v进栈p=adjlist[j].firstedge;}}if(j=vertexNum) top--;}
}
//求连通分量数，判断图的连通性
void ALGraph::CountComp(ALGraph g)
{int count=0;int n=g.vertexNum;for(int v=0;v<n;v++){if(visited[v]==0){count++;g.DFSL(v);}}if(count==1) cout<<endl<<"改图是连通的！"<<endl;else cout<<endl<<"改图不连通，连通分量数为："<<count<<endl;
}
int main()
{int a[9]={0,1,2,3,4,5,6,7,8};ALGraph gr=ALGraph(a,9);//初始化表头gr.createGraph(0,2);gr.createGraph(0,1);gr.createGraph(1,4);gr.createGraph(1,3);gr.createGraph(2,6);gr.createGraph(2,5);gr.createGraph(5,6);gr.createGraph(3,7);gr.createGraph(4,7);gr.createGraph(7,8);gr.displayGraph(9);for(int i=0;i<MaxSize;i++)visited[i]=0;gr.DFSL1(0);//gr.CountComp(gr);return 0;
}