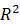TCP是什么?
TCP(Transmission Control Protocol 传输控制协议)是一种面向连接(连接导向)的、可靠的、 基于IP的传输层协议。TCP在IP报文的协议号是6。TCP是一个超级麻烦的协议,而它又是互联网的基础,也是每个程序员必备的基本功。首先来看看OSI的七层模型:
我们需要知道TCP工作在网络OSI的七层模型中的第四层——Transport层,IP在第三层——Network层,ARP 在第二层——Data Link层;在第二层上的数据,我们把它叫Frame,在第三层上的数据叫Packet,第四层的数 据叫Segment。 同时,我们需要简单的知道,数据从应用层发下来,会在每一层都会加上头部信息,进行 封装,然后再发送到数据接收端。这个基本的流程你需要知道,就是每个数据都会经过数据的封装和解封 装的过程。 在OSI七层模型中,每一层的作用和对应的协议如下:
TCP是一个协议,那这个协议是如何定义的,它的数据格式是什么样子的呢?要进行更深层次的剖析,就 需要了解,甚至是熟记TCP协议中每个字段的含义。哦,来吧。
上面就是TCP协议头部的格式,由于它太重要了,是理解其它内容的基础,下面就将每个字段的信息都详 细的说明一下。
Source Port和Destination Port:分别占用16位,表示源端口号和目的端口号;用于区别主机中的不同进程, 而IP地址是用来区分不同的主机的,源端口号和目的端口号配合上IP首部中的源IP地址和目的IP地址就能唯一 的确定一个TCP连接;
Sequence Number:用来标识从TCP发端向TCP收端发送的数据字节流,它表示在这个报文段中的的第一个数据 字节在数据流中的序号;主要用来解决网络报乱序的问题;
Acknowledgment Number:32位确认序列号包含发送确认的一端所期望收到的下一个序号,因此,确认序号应 当是上次已成功收到数据字节序号加1。不过,只有当标志位中的ACK标志(下面介绍)为1时该确认序列号的字 段才有效。主要用来解决不丢包的问题;
Offset:给出首部中32 bit字的数目,需要这个值是因为任选字段的长度是可变的。这个字段占4bit(最多能 表示15个32bit的的字,即4*15=60个字节的首部长度),因此TCP最多有60字节的首部。然而,没有任选字段, 正常的长度是20字节;
TCP Flags:TCP首部中有6个标志比特,它们中的多个可同时被设置为1,主要是用于操控TCP的状态机的,依次 为URG,ACK,PSH,RST,SYN,FIN。每个标志位的意思如下:
URG:此标志表示TCP包的紧急指针域(后面马上就要说到)有效,用来保证TCP连接不被中断,并且督促 中间层设备要尽快处理这些数据;
ACK:此标志表示应答域有效,就是说前面所说的TCP应答号将会包含在TCP数据包中;有两个取值:0和1, 为1的时候表示应答域有效,反之为0;
PSH:这个标志位表示Push操作。所谓Push操作就是指在数据包到达接收端以后,立即传送给应用程序, 而不是在缓冲区中排队;
RST:这个标志表示连接复位请求。用来复位那些产生错误的连接,也被用来拒绝错误和非法的数据包;
SYN:表示同步序号,用来建立连接。SYN标志位和ACK标志位搭配使用,当连接请求的时候,SYN=1, ACK=0;连接被响应的时候,SYN=1,ACK=1;这个标志的数据包经常被用来进行端口扫描。扫描者发送 一个只有SYN的数据包,如果对方主机响应了一个数据包回来 ,就表明这台主机存在这个端口;但是由于这 种扫描方式只是进行TCP三次握手的第一次握手,因此这种扫描的成功表示被扫描的机器不很安全,一台安全 的主机将会强制要求一个连接严格的进行TCP的三次握手;
FIN: 表示发送端已经达到数据末尾,也就是说双方的数据传送完成,没有数据可以传送了,发送FIN标志 位的TCP数据包后,连接将被断开。这个标志的数据包也经常被用于进行端口扫描。
Window:窗口大小,也就是有名的滑动窗口,用来进行流量控制;这是一个复杂的问题,这篇博文中并不会进行 总结的;
好了,基本知识都已经准备好了,开始下一段的征程吧。
三次握手又是什么?
TCP是面向连接的,无论哪一方向另一方发送数据之前,都必须先在双方之间建立一条连接。在TCP/IP协议中,TCP 协议提供可靠的连接服务,连接是通过三次握手进行初始化的。三次握手的目的是同步连接双方的序列号和确认号 并交换 TCP窗口大小信息。这就是面试中经常会被问到的TCP三次握手。只是了解TCP三次握手的 概念,对你获得一份工作是没有任何帮助的,你需要去了解TCP三次握手中的一些细节。先来看图说话。
多么清晰的一张图。
1.第一次握手:建立连接。客户端发送连接请求报文段,将SYN位置为1,Sequence Number为x;然后,客户端进入SYN_SEND状态,等待服务器的确认;
2.第二次握手:服务器收到SYN报文段。服务器收到客户端的SYN报文段,需要对这个SYN报文段进行确认,设置Acknowledgment Number为x+1(Sequence Number+1);同时,自己自己还要发送SYN请求信息,将SYN位置为1,Sequence Number为y;服务器端将上述所有信息放到一个报文段(即SYN+ACK报文段)中,一并发送给客户端,此时服务器进入SYN_RECV状态;
3.第三次握手:客户端收到服务器的SYN+ACK报文段。然后将Acknowledgment Number设置为y+1,向服务器发送ACK报文段,这个报文段发送完毕以后,客户端和服务器端都进入ESTABLISHED状态,完成TCP三次握手。
完成了三次握手,客户端和服务器端就可以开始传送数据。以上就是TCP三次握手的总体介绍。
那四次分手呢?
当客户端和服务器通过三次握手建立了TCP连接以后,当数据传送完毕,肯定是要断开TCP连接的啊。那对于TCP的断开连接,这里就有了神秘的“四次分手”。
1.第一次分手:主机1(可以使客户端,也可以是服务器端),设置Sequence Number和Acknowledgment Number,向主机2发送一个FIN报文段;此时,主机1进入FIN_WAIT_1状态;这表示主机1没有数据要发送给主机2了;
2.第二次分手:主机2收到了主机1发送的FIN报文段,向主机1回一个ACK报文段,Acknowledgment Number为Sequence Number加1;主机1进入FIN_WAIT_2状态;主机2告诉主机1,我也没有数据要发送了,可以进行关闭连接了;
3.第三次分手:主机2向主机1发送FIN报文段,请求关闭连接,同时主机2进入CLOSE_WAIT状态;
4.第四次分手:主机1收到主机2发送的FIN报文段,向主机2发送ACK报文段,然后主机1进入TIME_WAIT状态;主机2收到主机1的ACK报文段以后,就关闭连接;此时,主机1等待2MSL后依然没有收到回复,则证明Server端已正常关闭,那好,主机1也可以关闭连接了。
至此,TCP的四次分手就这么愉快的完成了。当你看到这里,你的脑子里会有很多的疑问,很多的不懂,感觉很凌乱;没事,我们继续总结。
为什么要三次握手?
既然总结了TCP的三次握手,那为什么非要三次呢?怎么觉得两次就可以完成了。那TCP为什么非要进行三次连接呢?在谢希仁的《计算机网络》中是这样说的:
为了防止已失效的连接请求报文段突然又传送到了服务端,因而产生错误。
在书中同时举了一个例子,如下:
"已失效的连接请求报文段”的产生在这样一种情况下:client发出的第一个连接请求报文段并没有丢失,而是在某个网络结点长时间的滞留了,以致延误到连接释放以后的某个时间才到达server。本来这是一个早已失效的报文段。但server收到此失效的连接请求报文段后,就误认为是client再次发出的一个新的连接请求。于是就向client发出确认报文段,同意建立连接。假设不采用“三次握手”,那么只要server发出确认,新的连接就建立了。由于现在client并没有发出建立连接的请求,因此不会理睬server的确认,也不会向server发送数据。但server却以为新的运输连接已经建立,并一直等待client发来数据。这样,server的很多资源就白白浪费掉了。采用“三次握手”的办法可以防止上述现象发生。例如刚才那种情况,client不会向server的确认发出确认。server由于收不到确认,就知道client并没有要求建立连接。"
这就很明白了,防止了服务器端的一直等待而浪费资源。
为什么要四次分手?
那四次分手又是为何呢?TCP协议是一种面向连接的、可靠的、基于字节流的运输层通信协议。TCP是全双工 模式,这就意味着,当主机1发出FIN报文段时,只是表示主机1已经没有数据要发送了,主机1告诉主机2, 它的数据已经全部发送完毕了;但是,这个时候主机1还是可以接受来自主机2的数据;当主机2返回ACK报文 段时,表示它已经知道主机1没有数据发送了,但是主机2还是可以发送数据到主机1的;当主机2也发送了FIN 报文段时,这个时候就表示主机2也没有数据要发送了,就会告诉主机1,我也没有数据要发送了,之后彼此 就会愉快的中断这次TCP连接。如果要正确的理解四次分手的原理,就需要了解四次分手过程中的状态变化。
FIN_WAIT_1: 这个状态要好好解释一下,其实FIN_WAIT_1和FIN_WAIT_2状态的真正含义都是表示等 待对方的FIN报文。而这两种状态的区别是:FIN_WAIT_1状态实际上是当SOCKET在ESTABLISHED状态时, 它想主动关闭连接,向对方发送了FIN报文,此时该SOCKET即进入到FIN_WAIT_1状态。而当对方回应ACK报 文后,则进入到FIN_WAIT_2状态,当然在实际的正常情况下,无论对方何种情况下,都应该马上回应ACK 报文,所以FIN_WAIT_1状态一般是比较难见到的,而FIN_WAIT_2状态还有时常常可以用netstat看到。 (主动方)
FIN_WAIT_2:上面已经详细解释了这种状态,实际上FIN_WAIT_2状态下的SOCKET,表示半连接,也即 有一方要求close连接,但另外还告诉对方,我暂时还有点数据需要传送给你(ACK信息),稍后再关闭连接。 (主动方)
CLOSE_WAIT:这种状态的含义其实是表示在等待关闭。怎么理解呢?当对方close一个SOCKET后发送FIN 报文给自己,你系统毫无疑问地会回应一个ACK报文给对方,此时则进入到CLOSE_WAIT状态。接下来呢,实 际上你真正需要考虑的事情是察看你是否还有数据发送给对方,如果没有的话,那么你也就可以 close这个 SOCKET,发送FIN报文给对方,也即关闭连接。所以你在CLOSE_WAIT状态下,需要完成的事情是等待你去关 闭连接。(被动方)
LAST_ACK: 这个状态还是比较容易好理解的,它是被动关闭一方在发送FIN报文后,最后等待对方的ACK报 文。当收到ACK报文后,也即可以进入到CLOSED可用状态了。(被动方)
TIME_WAIT: 表示收到了对方的FIN报文,并发送出了ACK报文,就等2MSL后即可回到CLOSED可用状态了。 如果FINWAIT1状态下,收到了对方同时带FIN标志和ACK标志的报文时,可以直接进入到TIME_WAIT状态,而无 须经过FIN_WAIT_2状态。(主动方)
CLOSED: 表示连接中断。






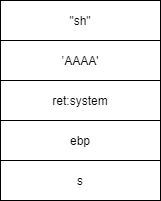

![【PWN · ret2libc】[2021 鹤城杯]babyof](https://img-blog.csdnimg.cn/6c95d5c7027a44daade842236b7345c9.png)