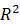在前面的文章里，已经带大伙了解了概率论的概率事件类型，以及针对某些事件的发生概率，以及针对全部场景的某事件的发生概率等基本知识。不过对于统计学专业来说，或者实际应用来说，接触最多的还是离散型和连续型概率，以及分析其概率密度与分布函数。所以说这里的内容可以算是概率论真正的支撑核心和基石。
无论你做数据分析，还是说人工智能方向，这是你应该打好的基础中的基础。

离散型及连续型概率模型的基本定义

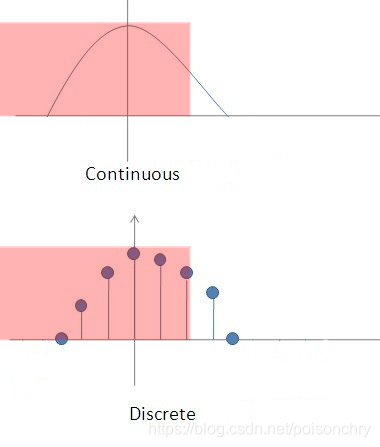
在研究生阶段，或者说在实际的工作阶段，经常可以看到关于连续和离散的讨论。我这里不想过多的讨论这个问题，只是简单的说一下，离散型，就相对于散数列，而连续型本质上是运动变化的连续描述。所以把数学上经常见到的两种不同类型的数据做到一张图表上，就是下面这个样子。

这是一张连续信号和离散信号的表达方式。对于概率来说，由于不存在 $<0$ 的情况，所以其各自的函数图就表现为：

那么根据概率的一般规律或者说属性，那就是针对定义域上的全部事件概率之和为1。那么对于离散型我们就可以知道，

F { X ≤ x r i g h t m o s t } = P 1 + P 2 + P 3 + ⋯ + P n = 1 F\left \{ X \leq x_{rightmost} \right \} = P_1 + P_2 + P_3 + \cdots + P_n = 1 F{X≤xrightmost​}=P1​+P2​+P3​+⋯+Pn​=1

即，把每个点的事件概率连续相加；而连续型，则是对函数图像求积分

$$F(x)={\int }_a^{b}f(x)dx=1$$

那么，一般在讨论到概率分布函数，即概率累计函数$F(X)$ 的时候，我们在上面那个概率分布图画一个向左侧覆盖的框。

框里所覆盖的部分，就是对样本事件概率的加和，即：

$$F(X)=\sum _{x_k\le x}{P}_k$$

所以，从以上不难得出，如果样本覆盖覆盖范围，$F(X<x_0)$ ，即$F(X)$取值范围不包括概率事件最左侧的样本概率，那么得出的累计概率(即分布函数)为0。

所以很容易求证出以下两条性质：

• $F(-\infty )=0$
• $F(+\infty )=1$

什么是概率模型的概率密度与概率分布函数

我个人不太喜欢从教科书的定义出发去理解概率密度与概率分布函数。既然它们的函数意义与微积分一样，那么不如直接从微积分的定义出发去理解函数的概率密度与概率分布更为方便。

通常提到概率密度，一般针对连续型的概率。我这里单刀直入，从概率分布函数（概率累加函数）的演算性质，它所对应的就是定积分概念里的求函数面积的过程。因此，从定积分的概念出发，很容易把概率的密度函数，和概率的分布函数统一到定积分里的导函数 $f(x)$ 与原函数 $F(X)$这一概念里。

当然，对于连续型：

$$F(X)={\int }_a^{b}f(x)dx$$

• $F(X)$ 是定积分里的原函数，也是概率里的分布函数
• $f(x)$ 是定积分里的导函数，也是概率里的概率密度函数

这样，我们把概念统一在一起后，对于理解离散型、连续型概率模型的概率密度与概率分布函数就显然简单太多了，因为我们可以把很多在定积分里，甚至不定积分里适用的工具全都拿到连续概率里，对我们来说无非求“面积/斜率”，显然这里用微积分工具明显更容易理解。

积分换元法与概率中的换元计算

直接看公式不是很容易理解，所以我也不是很理解国内的教科书为什么总喜欢跳过重要的基础知识点。这个，是连续型概率的重要知识点。所以我这里补充一些积分换元法的知识点，从而能让你从更为直观的角度理解概率论中连续型概率的换元运算背后的数学逻辑。

首先从链式法则出发，当一个函数是复合函数 $(g\circ f)(x)$ 对它的求导，等于：

$$F(X{)}^{\prime }=(g\circ f{)}^{\prime }(x)=g^{\prime }(f(x))f^{\prime }(x)$$

所以针对复合函数的积分，也可以根据导数的链式法则进行扩展，于是有：

$${\int }_a^{b}F(X{)}^{\prime }dX={\int }_{\alpha }^{\beta }{g}^{\prime }(f(t))f^{\prime }(t)dt$$

只不过需要注意，就是积分项 $dX$ 换到了 $dt$，所以导致了积分区域也会跟着一起发生改变。接着，然后我们换一种写法，令$F^{\prime }(X)=f(x)$, $f(t)=\phi (t)$，于是得到了第二类积分换元法，

$${\int }_a^{b}f(x)dx={\int }_{\alpha }^{\beta }f[\phi (t)]{\phi }^{\prime }(t)dt$$

这里并不难，难得是对数学符号的理解，你如果反应慢，建议多花点时间看一看，自己手动推导一遍看看。至于关键的 $\alpha$ $\beta$，应该取什么值的问题，这里用到的就是反函数的概念了，即：

$$\phi (\alpha )=a\to \alpha ={\phi }^{-1}(a)$$
$$\phi (\beta )=b\to \beta ={\phi }^{-1}(b)$$

然后，你再对比一下概率论里提到这部分的章节，是不是就理解了该死的概率换元公式，到底怎么得来的了吧。

$$f_Y(y)=f_X(h(y))|h^{\prime }(y)|$$

除了取绝对，其他简直一模一样。所以，你应该记住这里的概念，之后遇到类似的题目时，这些概念会成为我们解题的重要手段。

然后，跟其他章节里一样，我们来做点习题吧。

一些相关例题

1. 离散型随机变量、分布函数

盒中有6个球，其中4个白球，2个黑球，从中任取2个球，求：

• （1）抽到白球数X的分布律
• （2）随机变量X的分布函数

解（1）
所谓分布律，是指每一种样本的概率集合（Distribution），所以先分析白球的样本，X取值范围可以是：0，1，2
P { X = 0 } = C 4 0 C 2 2 C 6 2 = 1 15 P \left \{ X = 0 \right \} = \frac{C_4^0 C_2^2}{C_6^2} = \frac{1}{15} P{X=0}=C62​C40​C22​​=151​
P { X = 1 } = C 4 1 C 2 1 C 6 2 = 8 15 P \left \{ X = 1 \right \} = \frac{C_4^1 C_2^1}{C_6^2} = \frac{8}{15} P{X=1}=C62​C41​C21​​=158​
P { X = 2 } = C 4 2 C 2 0 C 6 2 = 6 15 P \left \{ X = 2 \right \} = \frac{C_4^2 C_2^0}{C_6^2} = \frac{6}{15} P{X=2}=C62​C42​C20​​=156​

然后绘制样本概率表

X	0	1	2
P	1/15	8/15	6/15

解（2）
根据上题中的样本概率表，我们可以得出概率累加函数（或者说分布函数）

即：

$$F(X)=\{\begin{array}{cc}0& x<0\\ 1/15& 0\le x<1\\ 9/15& 1\le x<2\\ 1& 2\le x\end{array}$$

这里的x并非取值范围。而是x处于坐标轴上什么位置，向左$\sum$的计算。即：

2. 离散型随机变量函数的分布

设随机变量X的分布律如下：

X	-1	0	1	2
P	0.4	0.3	0.2	0.1

• （1）$U=X-1$ 的分布律
• （2）$W=X^2$ 的分布律

解：

首先计算新分布函数的分布律，根据题目给出的公式，我们有：

P	0.4	0.3	0.2	0.1
X	-1	0	1	2
U	-2	-1	0	1
W	1	0	1	4

所以，我们可以根据上表，分别做出（1）和（2）的分布律

解（1）

U	-2	-1	0	1
P	0.4	0.3	0.2	0.1

解（2）

W	1	0	1	4
P	0.4	0.3	0.2	0.1

这里要稍微调整一下，于是有了：

W	0	1	4
P	0.3	0.6	0.1

3. 连续型的概率密度、分布函数

设连续型随机变量X的概率密度函数为 $f(x)=\{\begin{array}{cc}a+x^2& 0\le x<1\\ 0& else\end{array}$ 求
(1). 常数 a
(2). P { X > = 0.5 } P \left \{ X >= 0.5 \right \} P{X>=0.5}
(3). 分布函数F(X)

解（1）

从概率密度函数的定义出发，我们有：

$$\int f(x)dx=1\to {\int }_{else}f(x)dx+{\int }_0^1(a+x^2)dx=1$$

根据密度函数f(x)给出的条件，可以知道上式可以简化为：

$${\int }_0^1(a+x^2)dx=1$$

然后根据导积分的运算规则，获得原函数为：

$${\int }_0^1(a+x^2)dx={(ax+\frac{1}{3}{x}^3)|}_0^1=1$$

代入上限和下限后，可以得到

$$a+\frac{1}{3}=1\to a=\frac{2}{3}$$

解（2）
由于上面已经得到了 a=2/3，所以可以得到概率密度函数为：

$$f(x)=\{\begin{array}{cc}\frac{2}{3}+x^2& 0\le x<1\\ 0& else\end{array}$$

P { X > = 0.5 } P \left \{ X >= 0.5 \right \} P{X>=0.5} 即求解对于连续型概率，样本大于等于0.5后出现的事件概率，即对概率密度函数求积的过程。于是有：

P { X > = 0.5 } = ∫ 0.5 + ∞ f ( x ) d x = ∫ 0.5 1 f ( x ) d x + ∫ 1 ∞ f ( x ) d x P \left \{ X >= 0.5 \right \} = \int_{0.5}^{+\infty} f(x) dx = \int_{0.5}^{1} f(x) dx + \int_1^{\infty} f(x) dx P{X>=0.5}=∫0.5+∞​f(x)dx=∫0.51​f(x)dx+∫1∞​f(x)dx

根据题干给出的条件，可以知道 ${\int }_1^{\infty }f(x)dx=0$，所以问题简化为：

P { X > = 0.5 } = ∫ 0.5 1 f ( x ) d x = ∫ 0.5 1 [ 2 3 + x 2 ] d x P \left \{ X >= 0.5 \right \} = \int_{0.5}^{1} f(x) dx =\int_{0.5}^{1} [\frac{2}{3} + x^2]dx P{X>=0.5}=∫0.51​f(x)dx=∫0.51​[32​+x2]dx

然后根据导积分的运算规则，获得：

P { X > = 0.5 } = ( 2 3 x + 1 3 x 3 ) ∣ 0.5 1 = 5 8 P \left \{ X >= 0.5 \right \} = \left. (\frac{2}{3}x + \frac{1}{3} x^3) \right |_{0.5}^{1} = \frac{5}{8} P{X>=0.5}=(32​x+31​x3)∣∣∣∣​0.51​=85​

解（3）

我们根据以上各题，可以轻易的得到分布函数F(X)为

$$F(X)=\{\begin{array}{cc}0& x<0\\ \frac{2}{3}x+\frac{1}{3}{x}^3& 0\le x<1\\ 1& 1\le x\end{array}$$

需要记住的是 F(X) 与 f(x) 是导数和原函数的关系。

4. 连续型随机变量函数的分布

设随机变量X的概率密度为 $f(x)=\{\begin{array}{cc}x/8& 0<x<4\\ 0& else\end{array}$ 求Y = 2X + 8的概率密度。

解

f(x) 是关于X的概率密度函数，所以要先得到关于X的分布函数，再更新Y的分布函数，然后对Y求导可以得到Y的密度函数，于是遵从这个思想，我们可以做如下解题过程。

（1）：先从X的密度函数出发，得到关于X的分布函数

$$F_x(X)=\{\begin{array}{cc}\frac{x^2}{16}& 0<x<4\\ 0& else\end{array}$$

（2）：从关于Y的分布函数出发，得到关于X的分布函数替代式： X = (Y - 8) / 2 然后带入到上面的公式去：

$$F_y(Y)=\{\begin{array}{cc}(\frac{Y-8}{2}{)}^2/16& 0<(\frac{Y-8}{2})/16<4\\ 0& else\end{array}$$

（3）：对上式化简一下：

$$F_y(Y)=\{\begin{array}{cc}(\frac{Y-8}{2}{)}^2/16& 8<Y<16\\ 0& else\end{array}$$

（4）：对上式求导后，可以得到关于Y的概率密度函数。另外，由于$F_y(Y)$是复合函数，所以使用链式法则：

$$[(\frac{Y-8}{2}{)}^2/16{]}^{\prime }=\frac{2}{16}(\frac{Y-8}{2})\frac{1}{2}=\frac{Y-8}{32}$$

于是，

$$f_y(Y)=\{\begin{array}{cc}\frac{Y-8}{32}& 8<Y<16\\ 0& else\end{array}$$

这里你可以尝试使用一下公式法进行替代，不过我个人比较推荐从定义入手，毕竟这样不容易错。