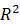提示:写完文章后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
- 欧拉常数
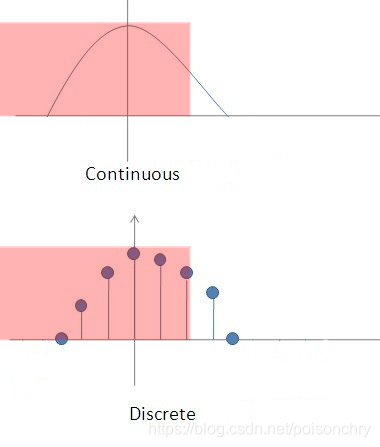
- 连续型随机变数与概率密度函数
- 正态分布
- 标准正态分步
- 检验
- t检验
- t假设
在我们将离散型数据的数值放大到无限,也就是讨论所谓的极限时,
欧拉常数

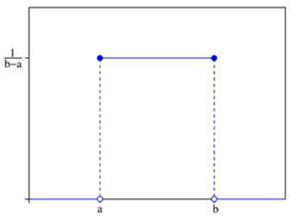
连续型随机变数与概率密度函数

均值及方差:

正态分布
“呈现带有误差现象的数据大多可用正态分布来表示”。
标准正态分步


推测统计
推测统计分为两个重要模块,一是通过研究样本对母集团做出概率预测的“推算”;二是针对已知数据的差值,找出产生差值原因的“检验”。

上面求出的“71.804kg~72.196kg”的范围在统计学上被称作95%的置信区间(是指由样本统计量所构造的总体参数的估计区间。
检验
统计学中的检验是一种合理判断数据是否存在异常的手段。
用统计学研究事物时,(一般来说)有95%概率发生的事件被视为“发生概率较大”的事件,而除此之外的事件被视为“异常”。
39分钟的时间在所测算的时间范围内,不算是异常情况。也就是说,“X=39”这一数据,包含在“μ=30”与数据整合后的数据范围内。
t检验

顺便说一句,有名的t检验是利用了t分布(由于在实际工作中,标准差(σ)是未知的,常用S作为σ的估算值,为了与μ变换区别,称为t变换,统计量t值的分布称为t分布。——编者注)进行的检验。而呈正态分布的母集团中抽出的数据样本呈标准正态分布(当数据量在数百甚至数千以上时,t分布与标准正态分布几乎一致)就十分接近于t分布。
t假设
T检验的适用条件为样本分布符合正态分布。
T检验的应用条件:
当样本例数较小时,要求样本取自正态总体;
做两样本均数比较时,还要求两样本的总体方差相
等。
单侧检验与双侧检验
• 在进行t检验时,如果其目的在于检验两个总体均数是否相等,即为双侧检验。 例如检验某种新降压药与常用降压药效力是否相同?就是说,新药效力可能比旧药好,也可能比旧药差,或者力相同,都有可能。
• 如果我们已知新药效力不可能低于旧药效力,例如磺胺药+磺胺增效剂从理论上推知其效果不可能低于单用磺胺药,这时,无效假设为H0:μ1=μ2, 备择假设为H1: μ1>μ2 , 统计上称为单侧检验
常以样本的标准差代替总体的标准差进行计算。
,如果你知道总体方差,统计量就服从正态分布,如果不知道总体方差,那个统计量就服从 [公式] 分布。