Hypothesis Testing
- 1.中心极限定理Central Limit Theorem
- 2.假设检验概念
- 2.1 零假设与备则假设
- 2.2 如何制定决策规则
- 3.假设性检验步骤
- 3.1假设检验框架
- 3.2术语定义
- 3.3 proportion test步骤
- 3.4 符号检验 sign test
1.中心极限定理Central Limit Theorem
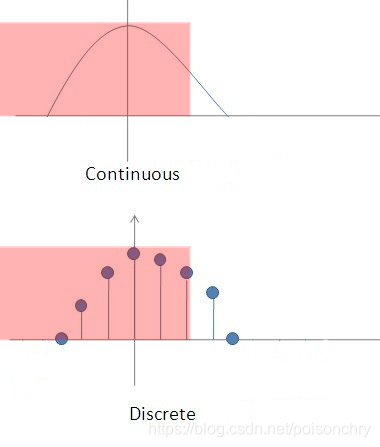
当总体是非正态分布且样本容量足够大时,使用正态分布来近似任何统计量的抽样分布。
两种应用:
1.1 X ˉ \bar{X} Xˉ的抽样分布
•考虑从一个具有平均偏差μ和标准偏差σ的总体(任何总体)中选择的n个观察的随机样本。当n够大(n≥30)、 X ˉ \bar{X} Xˉ的抽样分布将近似正态分布均值μ和标准差 σ n \frac{σ}{\sqrt{n}} nσ。象征性地, X ˉ ≈ ( μ , σ n ) \bar{X}\approx(\mu,\frac{σ}{\sqrt{n}}) Xˉ≈(μ,nσ),近似。
•如果随机样本n是从正态整体中选取,则 X ˉ \bar{X} Xˉ的抽样分布是正态分布; X ˉ ∼ ( μ , σ n ) \bar{X}\sim(\mu,\frac{σ}{\sqrt{n}}) Xˉ∼(μ,nσ)精确。
1.2 p ^ \hat{p} p^的抽样分布
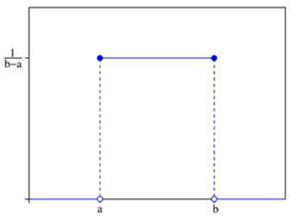
X : 具有感兴趣特征的元素的数量是一个二项式随机变量, p ^ = x n \hat{p}=\frac{x}{n} p^=nx的抽样分布实际上遵循二项分布。如果样本大小是足够大的,那么可以用正常的经验法则来近似: n > 25,np > 5,以及 q = 1-p 的 nq > 5
随机变量标准化

例子


1.3 二项的正态逼近
•如果X ~ Bin(n, p)且n足够大,则可近似为Y,其中 Y ∼ N ( μ = n p , σ = n p q ) Y\sim N(\mu=np,\sigma=\sqrt{npq}) Y∼N(μ=np,σ=npq)
•经验法则:n > 25, np > 5,和nq > 5
•校正连续性调整
•当离散分布近似为连续分布时,需要连续性校正。从离散随机变量X的值上加或减0.5是连续性校正。
•例如,如果X ~ Bin(n=100, p=0.7),近似p (X > 25)。
P(X > 25) = 1 - P(X≤25.5)≈1 - P(Y≤25.5)
eg.假设从一个正在进行的生产过程中随机获得n = 100个相同类型的轮胎样本,其中8%的轮胎是有缺陷的。
•在这样一个样品中有超过10个轮胎有缺陷的确切概率是多少?

•在这样一个样品中,缺陷轮胎超过10个的近似概率是多少?

2.假设检验概念
2.1 零假设与备则假设
零假设 Null Hypothesis (H0)
H0是普遍接受的事实
使用=号指定,即使≤或≥
示例,H0: μ= 3
备择假设 Alternative Hypothesis(H1)
与零假设相反
如果H0被拒绝,通常代表了一个新的理论(研究问题)。
总是不等号:<、>、或≠
示例,H1:μ< 3

假设检验的四种可能结果

2.2 如何制定决策规则
临界值的方法 Critical value approach
如果测试统计量落在拒绝区域,则拒绝H0
P值即概率,反映某一事件发生的可能性大小。
- 如果 P<0.01,说明是较强的判定结果,拒绝假定的参数取值。
- 如果 0.01<P值<0.05,说明较弱的判定结果,拒接假定的参数取值。
- 如果 P值>0.05,说明结果更倾向于接受假定的参数取值
假定值的方法 P-value approach
如果假定值<α则否定H0
α=P(I类错误)
α在检验开始前被指定
典型值是0.01、0.25、0.05、0.10(常用为 0.05)
置信区间的方法 Confidence interval approach
如果空值(在H0中指定的值)位于置信区间之外,则拒绝H0
3.假设性检验步骤
3.1假设检验框架
对于每个假设检验,我们使用以下框架:
H
建立了两个假设:H0和H1。
A
陈述测试的假设,并证明这些假设从样本中是否有效。
T
陈述检验统计量,并且假设H0为真,它的分布。
说明哪些值反对H0。
找到测试统计量的观察值。
计算P值,表示在H0为真的情况下观察该样本(或更极端)的概率。
C
根据p值的大小权衡结论。
3.2术语定义
H
- Null hypothesis H0是默认的假设:我们当前认为是正确的。
- 假设H1是关于总体的新假设。
- 假设通常用未知的总体参数表示。例如H0:μ= 5。
- 如果是这样,那么备选假设可以采取两种形式:1边假设(H1:μ> 5或H1:μ< 5)或2边假设(H1:/= 5)。
- 我如何决定一个1或2边测试?这个决定不能受到数据的影响(“数据窥探”)——我们必须在进行实际测试之前明确假设。因此,我们总是使用双侧测试,除非我们有预先的证据(例如以前的报告)建议使用单侧测试。
A
- 这些假设对于测试的有效性是必要的。我们从样本中检查它们是否有效。
T
- 检验统计量τ是一个随机变量,其分布取决于未知参数。
- 从样本中计算出测试统计量τobs的观测值。
- 查看可调整的分布,以确定哪些值将与H1的H0争论。
- 假设检验涉及到一些关于随机变量的理论,其中每一个可能的值{T0}都作为H0的一些证据。假设检验根据观察值对证据和H0进行权衡。
p
- p值是在H0下观察到τ的概率,或更极端(或不寻常)的概率。
- p值小,要么表示H0为真,但样本非常罕见,要么表示H0为假。
- p值越小,H1对H0不利的证据越强。
- p值大表示样本与H0一致。
- 临界区域是使H0被拒绝的。
 C
C - “(零假设)是……从未被证明或建立,但可能被推翻,在实验的背景下。每一个实验的存在都只是为了给事实一个机会来反驳无效假设。(罗纳德·费舍尔,《实验设计》,1935年,第19页)。
没有最终的证据证明H0是对的还是错的。 - 结论是不‘接受’H0或H1,因为我们已经假设H0为真。也就是说,我们并没有证明H0是真的,而是在寻找证据来证明它是否是假的。
- I如果p值很小,说明存在不利于H0的证据。如果p值是不小,那么它表明数据是一致的H0
通过’小’,一个常见的惯例是,是也就是说,对于p < 0.05,我们建议有不利于H0的证据。

3.3 proportion test步骤
对于关于未知总体比例p的假设,我们执行以下步骤。
H H0: p = p0 vs H1: p < p0n次试验是独立的,概率为常数p。
T τ = X =在H0下成功的数量~ Bin(n, p0)
对于H1, x的小值会与H0争论。
观测值为x,
P P-value = P(x≤x)。
C衡量p值。经验法则是拒绝H0,因为p值< 0.05 =α。
P-values假定值:
如果备选假设是H1: p > p0,那么对于H1, x的较大值将与H0发生争论,因此对应的p值为p (X≥x)。
如果交替假设为双侧H1: p /= p0,那么对于H1, x的大小值都与H0相反,相关的p值为p (|x-np0|≥|x-np0|)。
在p0 = 12的特殊情况下,两边的p值降为
X > n/2时, P-value = 2P(X≥X)。
X < n/2时,P-value = 2P(X≤X)。
如果n很大,那么我们可以使用CLT(上周)来找到p值的近似值。我们找到近似的标准Y ~ N(np0, np0(1- p0)),然后使用R或标准化标准值并查找标准表。
IVF案例



3.4 符号检验 sign test
符号检验是一种巧妙的方法,它有效地扩大了比例检验的适用性。它允许“比例”检验用于检验关于平均值或中位数的假设。
我们从H0:µ=µ0(或H0:˜µ=˜µ0)H0: p + = 0.5,通过考虑的比例差异的迹象{签署(ξµ0)}这是积极的。
注意:如果任何观测值等于零假设值xi = l0,则从样本中消除它们。这假设只有几个’ 0 ',因为它有效地减少了样本大小。
假设单个样本x1, x2,…, xn取未知类型的连续分布。
我们想测试H0:µ=µ0(或H0:˜µ=˜µ0)。
如果我们假设分布是对称的,那么如果H0成立,每个观测值都等可能在H0之上或之下。
考虑不同符号的集合sign(x1 - µ0),sign(x2 - µ0)… …sign(xn - µ0)
定义X =关于Bin(n, p+)的+号数量,其中p+ = p(+差)。
那么H0:µ=µ0 就等于H0:P+=0.5
符号测试步骤

案例:freeze dried coffee