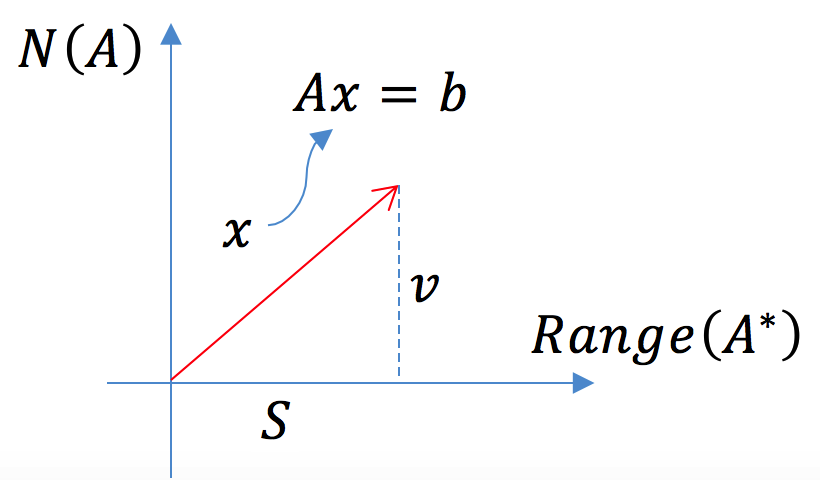
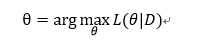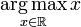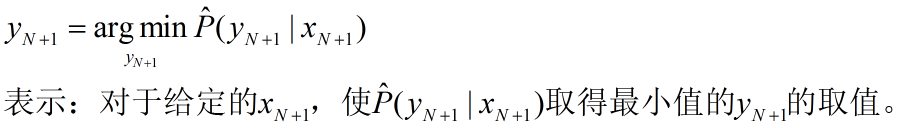背景

目前互联网已经进入了AI驱动业务发展的阶段，传统的机器学习开发流程基本是以下步骤：

数据收集->特征工程->训练模型->评估模型效果->保存模型，并在线上使用训练的有效模型进行预测。

这种方式主要存在两个瓶颈：模型更新周期慢，不能有效反映线上的变化，最快小时级别，一般是天级别甚至周级别。另外一个是模型参数少，预测的效果差；模型参数多线上predict的时候需要内存大，QPS无法保证。

针对这些问题，一般而言有两种解决方式：一种是采用On-line-learning的算法，一种采用一些优化的方法，在保证精度的前提下，尽量获取稀疏解，从而降低模型参数的数量。

传统的训练方法在模型训练上线后，一般是静态的，不会与线上的状况有任何的互动，加入预测错误，只能在下一次更新的时候完成修正，但是这个更新的时间一般比较长。

现实中为了及时对市场的变化进行反应，越来越多的业务选用在线学习方式直接处理流式数据、实时进行训练实时进行更新模型。

在线学习

在线学习算法的特点是：每来一个训练样本，就用该样本产生的loss和梯度对模型迭代一次，一个一个数据地进行训练，能够根据线上反馈数据，实时快速地进行模型调整，使得模型及时反映线上的变化，提高线上预测的准确率。因此可以处理大数据量训练和在线训练。常用的有在线梯度下降（OGD）和随机梯度下降（SGD）等，Online Learning的优化目标是使得整体的损失函数最小化，它需要快速求解目标函数的最优解。

现在做在线学习和CTR常常会用到逻辑回归（ Logistic Regression），google先后三年时间（2010年-2013年）从理论研究到实际工程化实现的FTRL（Follow-the-regularized-Leader）算法，在处理诸如逻辑回归之类的带非光滑正则化项（例如1范数，做模型复杂度控制和稀疏化）的凸优化问题上性能非常出色。

FTRL及工程实现

FTRL介绍

FTR是FTRL的前身，思想是每次找到让之前所有样本的损失函数之和最小的参数。FTRL，即 Follow The Regularized Leader，借鉴经典的TG，OGD , L1-FOBOS, L1-RDA 在之前的几个工作上产生的，主要出发点就是为了提高稀疏度且满足精度要求。FTRL 在FTL的优化目标的基础上，加入了正则化，防止过拟合。FTRL的损失函数一般也不容易求解，这种情况下，一般需要找一个代理的损失函数。代理损失函数需要满足以下条件：

代理损失函数比较容易求解，最好是有解析解。
代理损失函数求得的解，和原函数的解的差距越小越好

为了衡量条件2中的两个解的差距，引入regret的概念。如果一个在线学习算法可以保证其 regret 是 t 的次线性函数，那么随着训练样本的增多，在线学习出来的模型无限接近于最优模型。即随着训练样本的增加，代理损失函数和原损失函数求出来的参数的实际损失值差距越来越小。而毫不意外的，FTRL 正是满足这一特性。另一方面，现实中对于 sparsity，也就是模型的稀疏性也很看重。上亿的特征并不鲜见，模型越复杂，需要的存储、时间资源也随之升高，而稀疏的模型会大大减少预测时的内存和复杂度。另外稀疏的模型相对可解释性也较好，这也正是通常所说的 L1 正则化的优点。

工程实现

　　逻辑回归下的per-coordinate FTRL_Proximal的伪代码如下：

实现的时候，可在公式表达的基础上做了一些变换在实际数据集上再采用分布式并行加速。

　　四个参数的设定结合paper里的指导意见以及反复实验测试，找一组适合自己问题的参数就可以了。上面所谓的per-coordinate，其意思是FTRL是对w每一维分开训练更新的，每一维使用的是不同的学习速率，也是上面代码中lamda2之前的那一项。与w所有特征维度使用统一的学习速率相比，这种方法考虑了训练样本本身在不同特征上分布的不均匀性，如果包含w某一个维度特征的训练样本很少，每一个样本都很珍贵，那么该特征维度对应的训练速率可以独自保持比较大的值，每来一个包含该特征的样本，就可以在该样本的梯度上前进一大步，而不需要与其他特征维度的前进步调强行保持一致。

开源实现

目前已经有许多关于FTRL的开源实现，有基于多线程版本，基于参数服务器及MPI的分布式版本实现，可以跑在诸如yarn资源管理平台上，另外经调研一线互联网有采用基于实时计算引擎 Flink 的Alink实现在线学习。

如：Distributed FM and LR with parameter server ：https://github.com/CNevd/Difacto_DMLC

参考Python代码实现

# coding=utf-8import numpy as np
class LR(object):@staticmethoddef fn(w, x):'''决策函数为sigmoid函数'''return 1.0 / (1.0 + np.exp(-w.dot(x)))@staticmethoddef loss(y, y_hat):'''交叉熵损失函数'''return np.sum(np.nan_to_num(-y * np.log(y_hat) - (1 - y) * np.log(1 - y_hat)))@staticmethoddef grad(y, y_hat, x):'''交叉熵损失函数对权重w的一阶导数'''return (y_hat - y) * x
class FTRL(object):def __init__(self, dim, l1, l2, alpha, beta, decisionFunc=LR):self.dim = dimself.decisionFunc = decisionFuncself.z = np.zeros(dim)self.n = np.zeros(dim)self.w = np.zeros(dim)self.l1 = l1self.l2 = l2self.alpha = alphaself.beta = betadef predict(self, x):return self.decisionFunc.fn(self.w, x)def update(self, x, y):self.w = np.array([0 if np.abs(self.z[i]) <= self.l1 else (np.sign(self.z[i]) * self.l1 - self.z[i]) / (self.l2 + (self.beta + np.sqrt(self.n[i])) / self.alpha) for i in xrange(self.dim)])y_hat = self.predict(x)g = self.decisionFunc.grad(y, y_hat, x)sigma = (np.sqrt(self.n + g * g) - np.sqrt(self.n)) / self.alphaself.z += g - sigma * self.wself.n += g * greturn self.decisionFunc.loss(y, y_hat)def train(self, trainSet, verbos=False, max_itr=100000000, eta=0.01, epochs=100):itr = 0n = 0while True:for x, y in trainSet:loss = self.update(x, y)if verbos:print "itr=" + str(n) + "\tloss=" + str(loss)if loss < eta:itr += 1else:itr = 0if itr >= epochs:  # 损失函数已连续epochs次迭代小于etaprint "loss have less than", eta, " continuously for ", itr, "iterations"returnn += 1if n >= max_itr:print "reach max iteration", max_itrreturnclass TestData(object):def __init__(self, file, d):self.d = dself.file = filedef __iter__(self):with open(self.file, 'r') as f_in:for line in f_in:arr = line.strip().split()if len(arr) >= (self.d + 1):yield (np.array([float(x) for x in arr[0:self.d]]), float(arr[self.d]))if __name__ == '__main__':d = 4testData = TestData("train.txt", d)ftrl = FTRL(dim=d, l1=1.0, l2=1.0, alpha=0.1, beta=1.0)ftrl.train(testData, verbos=False, max_itr=100000, eta=0.01, epochs=100)w = ftrl.wprint wcorrect = 0wrong = 0for x, y in testData:y_hat = 1.0 if ftrl.predict(x) > 0.5 else 0.0if y == y_hat:correct += 1else:wrong += 1print "correct ratio", 1.0 * correct / (correct + wrong)

基于Flink 实现

Alink 是阿里巴巴基于实时计算引擎 Flink 研发的新一代机器学习算法平台，是业界首个同时支持批式算法、流式算法的机器学习平台，Alink 中提供了在线学习算法FTRL在Alink中的实现，主要流程如下：

具体代码实现逻辑如下：

● 建立特征处理管道，其包括StandardScaler和FeatureHasher，进行标准化缩放和特征哈希，最后得到了特征向量。

Pipeline featurePipeline = new Pipeline().add(new StandardScaler().setSelectedCols(numericalColNames)).add(new FeatureHasher().setSelectedCols(selectedColNames).setCategoricalCols(categoryColNames).setOutputCol(vecColName).setNumFeatures(numHashFeatures));// fit feature pipeline model// 构建特征工程流水线PipelineModel featurePipelineModel = featurePipeline.fit(trainBatchData);

● 准备数据集这里构建kafka之类的流式数据，并进行实时切分得到原始训练数据和原始预测数据，

// 准备流式数据集
CsvSourceStreamOp data = new CsvSourceStreamOp().setFilePath("http://alink-release.oss-cn-beijing.aliyuncs.com/data-files/avazu-ctr-train-8M.csv").setSchemaStr(schemaStr).setIgnoreFirstLine(true);// 这里可以采用kafaka数据源KafkaSourceStreamOp soure = new KafkaSourceStreamOp().setBootstrapServers("localhost:9092").setTopic("train_data_topic").setStartupMode("EARLIEST").setGroupId("");// 对于流数据源进行实时切分得到原始训练数据和原始预测数据SplitStreamOp splitter = new SplitStreamOp().setFraction(0.5).linkFrom(data);

● 训练出一个逻辑回归模型作为FTRL算法的初始模型，这是为了系统冷启动的需要。

LogisticRegressionTrainBatchOp lr = new LogisticRegressionTrainBatchOp()
.setVectorCol(vecColName)
.setLabelCol(labelColName)
.setWithIntercept(true)
.setMaxIter(10);BatchOperator<?> initModel = featurePipelineModel.transform(trainBatchData).link(lr);

● 在初始模型基础上进行FTRL在线训练；

// 在初始模型基础上进行FTRL在线训练       
FtrlTrainStreamOp model = new FtrlTrainStreamOp(initModel)
.setVectorCol(vecColName)
.setLabelCol(labelColName)
.setWithIntercept(true)
.setAlpha(0.1)
.setBeta(0.1)
.setL1(0.01)
.setL2(0.01)
.setTimeInterval(10)
.setVectorSize(numHashFeatures)
.linkFrom(featurePipelineModel.transform(splitter));

● 在FTRL在线模型的基础上，连接预测数据进行预测；/

FtrlPredictStreamOp predictResult = new FtrlPredictStreamOp(initModel) .setVectorCol(vecColName)              .setPredictionCol("pred").setReservedCols(new String[]{labelColName}).setPredictionDetailCol("details").linkFrom(model, featurePipelineModel.transform(splitter.getSideOutput(0)));

● 对预测结果流进行评估

// 对预测结果流进行评估
predictResult
.link( new EvalBinaryClassStreamOp().setLabelCol(labelColName).setPredictionCol("pred").setPredictionDetailCol("details").setTimeInterval(10)).link(new JsonValueStreamOp().setSelectedCol("Data").setReservedCols(new String[]{"Statistics"}).setOutputCols(new String[]{"Accuracy", "AUC", "ConfusionMatrix"}).setJsonPath(new String[]{".AUC", "$.ConfusionMatrixx"})  ).print();StreamOperator.execute();

编译打包

在开发打包成jar包的时候，遇到两个问题，一个是没有把依赖包导入到jar中，提交到flink集群的时候，任务找不到相关类，另外就是打包的时候包flink相关的包打进去了造成与flink lib中的jar包冲突，所以注意maven 打包排除 flink包，以免报错

部署flink集群

wget https://archive.apache.org/dist/flink/flink-1.13.0/flink-1.13.0-bin-scala_2.11.tgz
tar -xf flink-1.13.0-bin-scala_2.11.tgz && cd flink-1.13.0
./bin/start-cluster.sh

提交flink 任务

./bin/flink run -p 1 -c org.example.FTRLExample  FlinkOnlineProject-1.0-SNAPSHOT.jar

查看任务状态

提交任务到flink集群后可以通过flink web ui查看任务状态，一般如果是local模式运行，在浏览器输入 http://localhost:8081/ 就可以看到所有提交到flink 集群上的状态、以及checkpoint、反压之类的，如下图所示任务运行状态：

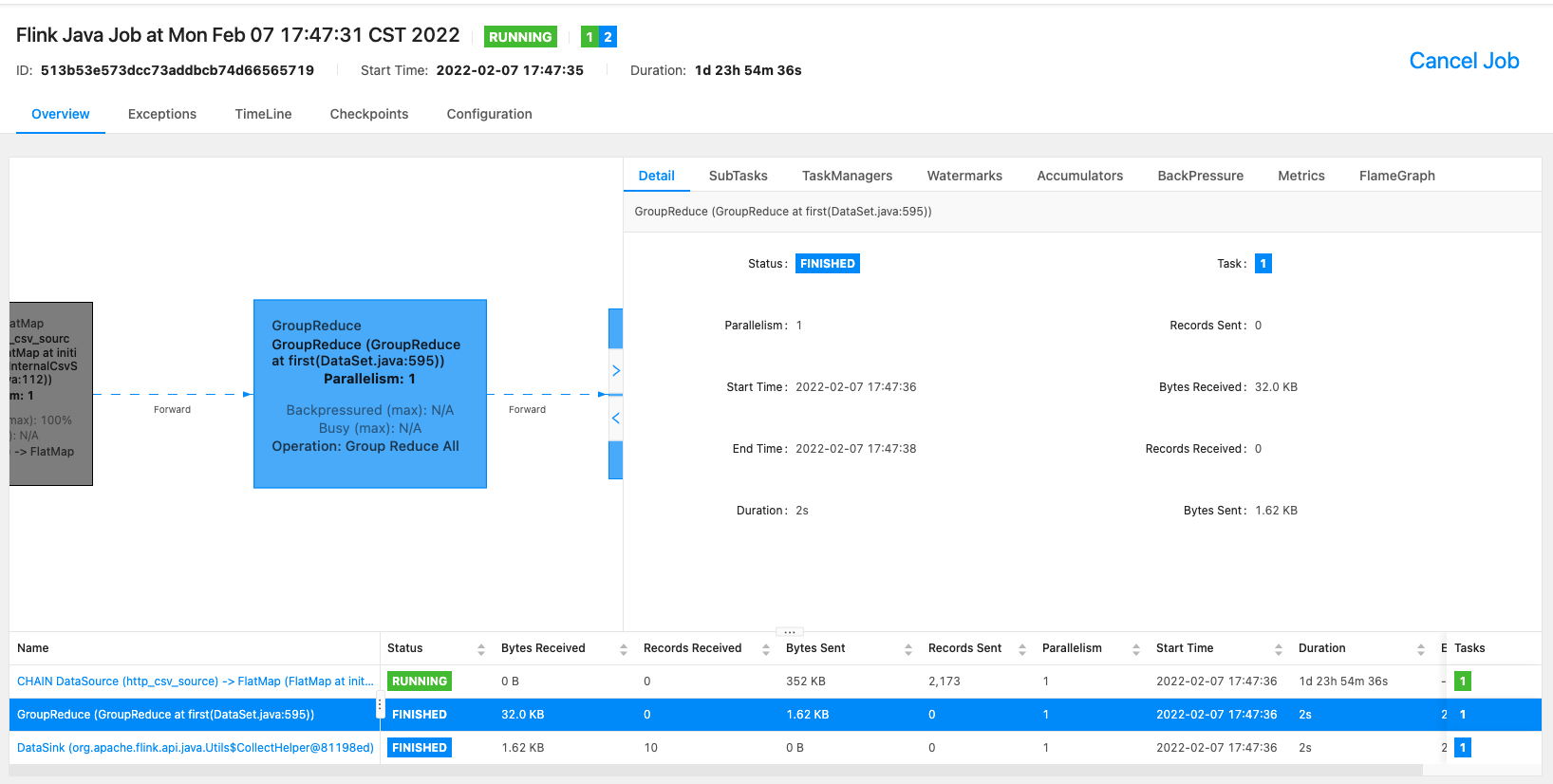
工程优化手段

内存优化

内存节省主要可以分为预测及训练两块主要的策略可以采取以下方式：

预测时候的内存节省：

L1范数加策略，训练结果w很稀疏，在用w做predict的时候节省了内存

训练时的内存节省：

在线丢弃训练数据中很少出现的特征(probabilistic feature inclusion）
浮点数重新编码
训练若干相似的模型，保证可以部分共享相关特征。
单值结构，多个模型公用一个特征存储，同时更新这个共有的特征结构
使用正负样本的数量来计算梯度的和
抽样训练集，选择更有价值的的样本

总结

以上是关于在线学习相关知识的总结和梳理，随着大数据时代的到来和人工智能的崛起，机器学习所能处理的场景更加广泛和多样，为了达到实时性的要求还需要直接对流式数据进行实时预测，在线训练已经成为一种趋势，国外从2010起就有相关探索，目前flink已经成为了事实上的标准，针对在线学习也有生产上的计算框架alink进行支持，其利用flink丰富的connector 、可扩展的operate、以及分布式部署能力能够很快的实现在线学习，已经在多个互联网大厂进行使用了。

针对性能这块，Flink是采用java语言进行开发的，目前调研Flink除了有基于JPython的python语言支持外，没有针对其它语言的开发，除了在Flink中有些公司为了性能等会使用 C++ 和 LLVM 实现的高性能 Flink Native 执行引擎等方式进行优化，通过java调用底层c++之类的实现。