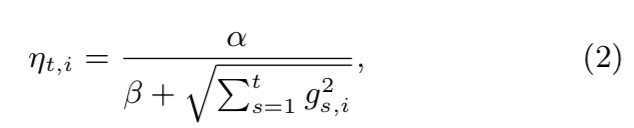本文主要是对FTRL算法来源、原理、应用的总结和自己的思考。
解决的问题
1、训练数据层面:数据量大、特征规模大
2、常用的LR和FM这类模型的参数学习,传统的学习算法是batch learning算法,无法有效地处理大规模的数据集,也无法有效地处理大规模的在线数据流
3、需要高效的online learning算法来解决这种问题
在线学习算法
SGD
w t + 1 = w t − n t g t w_{t+1} = w_t - n_tg_t wt+1=wt−ntgt
SGD的缺点
- 难以产生稀疏解: 简单的在线梯度下降很难产生真正稀疏的解。这里有两个疑问:
为什么SGD难以产生稀疏解?
找了网上有很多解释,我的理解为:
-
对于Batch+L1来说,直接会优化到cost function最小值,此时最小值对应的w为0。
-
但是不同于批量梯度下降,SGD每次更新不是沿着全局梯度进行下降,而是沿着某个样本的产生的梯度方向进行下降,整个寻优过程变得像是一个“随机” 查找的过程(SGD 中 Stochastic 的来历),这样 Online 最优化求解即使采用 L1 正则化的方式, 也很难产生稀疏解。
为什么稀疏解在工程上是重要的?
稀疏性在机器学习中是很看重的事情,尤其我们做工程应用,稀疏的特征会大大减少predict时的内存和复杂度(可以用tensorlfow的sparse tensor及scipy的csr_matrix等表示,减少内存)
做稀疏解的思路:
既然SGD不能直接得到稀疏解,我们可以将小于一定阈值的weight置为0
在L1范数的基础上做截断
缺点:
权重小,可能是确实是无用特征,还或者可能是该特征才刚被更新一次(例如训练刚开始的阶段、或者训练数据中包含该特征的样本数本来就很少)
Truncated Gradient(截断式梯度下降)

我的理解为:
1、当最优w真的在0时。因为 λ \lambda λ不断增大,最后必然存在一次迭代,使得计算出的w变号,这时w进行截断,设置为0
2、当最优w不在0时。因为刚开始 λ \lambda λ 较小,且每隔K次才判断是否截断。所以当w在0附近时, λ \lambda λ 的值不至于使w变号,此时不会进行截断
3、就参数来说,可以通过 θ \theta θ 和 λ \lambda λ来控制稀疏度,当这两个参数越大,解越稀疏
FOBOS
可以看作truncated gradient的一种特殊形式
将每一个数据的迭代过程,分解成一个经验损失梯度下降迭代和一个最优化问题
分解出的第二个最优化问题,有两项:第一项2范数那一项表示不能离第一步loss损失迭代结果太远,第二项是正则化项,用来限定模型复杂度抑制过拟合和做稀疏化等
RDA
非梯度下降类方法,属于更加通用的一个primal-dual algorithmic schema的一个应用
克服了SGD类方法所欠缺的exploiting problem structur
e,especially for problems with explicit regularization
能够更好地在精度和稀疏性之间做trade-off
FTRL
结合了FOBOS(好的精度)+ RDA(出色的稀疏性)两个方法的优点, 重点限定了:
新的迭代结果w不要离已迭代过的解太远(也即FTRL-Proximal中proximal的含义),或者离0太远(central)
FTRL算法原理
FTRL公式理解
w t + 1 = a r g m i n w ( ∑ s = 1 t g s ∗ w + 1 2 ∑ s = 1 t σ s ∣ ∣ w − w s ∣ ∣ 2 + λ ∣ ∣ w ∣ ∣ ) 其 中 t 为 迭 代 次 数 w 是 模 型 参 数 g 是 损 失 函 数 关 于 w 的 梯 度 w_{t+1} = \mathop {argmin}\limits_{w} (\sum_{s=1}^tg_s*w+\frac{1}{2}\sum_{s=1}^t\sigma_s||w-w_s||^2+\lambda||w||) \\其中t为迭代次数 \\w是模型参数 \\g是损失函数关于w的梯度 wt+1=wargmin(s=1∑tgs∗w+21s=1∑tσs∣∣w−ws∣∣2+λ∣∣w∣∣)其中t为迭代次数w是模型参数g是损失函数关于w的梯度
σ s \sigma_s σs定义为 ∑ s = 1 t σ s = 1 η t \sum_{s=1}^t\sigma_s = \frac{1}{\eta_t} ∑s=1tσs=ηt1, 其中 η t \eta_t ηt为t时刻的学习率,可以看到随着迭代次数的增多,学习率越来越小.
这里主要是为了理解这句话:
FTRL是结合了SGD的高精度并且能产生稀疏解。
总结:
- 公式左边两项等价于SGD
- 公式最后一项是L1正则,为了获取稀疏解
1、针对左边两项最小化,将左边两项对w求梯度:
∂ f ( w ) ∂ w = ∑ s = 1 t g s + ( w t + 1 − w s ) = 0 \frac{\partial f(w)}{\partial w} = \sum_{s=1}^tg_s+(w_{t+1}-w_s) = 0 ∂w∂f(w)=s=1∑tgs+(wt+1−ws)=0
2、对公式进行化简,得到:
1 η t w t + 1 − 1 η t − 1 w t = ( 1 η t − 1 η t − 1 ) w t − g t \frac{1}{\eta_t}w_{t+1} - \frac{1}{\eta_{t-1}} w_t = (\frac{1}{\eta_t} - \frac{1}{\eta_{t-1}})w_t-g_t ηt1wt+1−ηt−11wt=(ηt1−ηt−11)wt−gt
3、继续对公式化简,最终得到的就是SGD的公式
FTRL的工程实现

per-coordinate理解
- FTRL对w每一维分开训练更新的,每一维使用的是不同的学习速率,也是上面代码中lamda2之后的那一项
思考:FTRL为什么采用per-coordinate,而不是所有的w都是同一个学习率?
-
主要考虑了真实环境中训练样本本身在不同特征上分布的不均匀性,因为真实环境中大部分是高维稀疏的特征,如果包含w某一个维度特征的训练样本很少,每一个样本都很珍贵。
-
那么该特征维度对应的训练速率可以独自保持比较大的值,每来一个包含该特征的样本,就可以在该样本的梯度上前进一大步,而不需要与其他特征维度的前进步调强行保持一致。
工程实现中Memory saving策略(主要总结自参考资料)
predict时的memory saving
- L1范数加策略,训练结果w很稀疏,在用w做predict的时候节省了内存
Training时的memory saving:
-
数值重新编码
-
使用Bloom Filter进行特征筛选:在线丢弃训练数据中很少出现的特征(probabilistic feature inclusion),但是对于online set,对全数据进行pre-process查看哪些特征出现地很少、或者哪些特征无用,是代价很大的事情,所以需要训练的时候就做稀疏化
-
训练数据采样+权重:
- 思路: 先采样减少负样本数目,在训练的时候再用权重弥补负样本
- 在实际中,CTR远小于50%,所以正样本更加有价值。通过对训练数据集进行subsampling,可以大大减小训练数据集的大小
- 正样本全部采(至少有一个广告被点击的query数据),负样本使用一个比例r采样(完全没有广告被点击的query数据)。但是直接在这种采样上进行训练,会导致比较大的biased prediction
- 训练的时候,对样本再乘一个权重。权重直接乘到loss上面,从而梯度也会乘以这个权重。
参考资料
https://zhuanlan.zhihu.com/p/36410780
https://www.cnblogs.com/EE-NovRain/p/3810737.html
https://github.com/comadan/FM_FTRL/blob/master/FM_FTRL_machine.py
http://vividfree.github.io/%E6%9C%BA%E5%99%A8%E5%AD%A6%E4%B9%A0/2015/12/05/understanding-FTRL-algorithm
https://github.com/comadan/FM_FTRL/blob/master/FM_FTRL_machine.py
https://www.kaggle.com/c/avazu-ctr-prediction/discussion/10927